E R M eca(3) ? ER ? ´Oscillateur harmonique amorti PDF

1 Oscillateur harmonique

8 sept. 2013 élémentaire d'oscillateur harmonique: le système masse-ressort horizontal non amorti la mise en équation du mouvement de la masse et la ...

Oscillateur harmonique horizontal (cours) LE DISPOSITIF SOLIDE

½ (1). K est le coefficient de raideur du ressort. On l'exprime en N / m. 2- PENDULE ELASTIQUE LIBRE NON AMORTI. Un oscillateur élastique est constitué d

Cours de mécanique - M13-Oscillateurs

Nous étudierons dans ce chapitre en premier lieu l'oscillateur harmonique solide-ressort horizontale nous introduirons donc la force de rappel du ressort

Oscillateur harmonique

Exercice 1 : Ressort horizontal. 1. Représenter un système masse-ressort horizontal : • quand son élongation est maximale. • un quart de période plus tard

Phy 12a/12b Oscillateur harmonique : corrections 2013-2014

Deux ressorts sans masse de longueurs l1 et l2 au repos et de raideurs k1 et k2 sont accrochés bout à bout et tendus horizontalement entre deux murs distants de

Oscillateur harmonique

Oscillateur harmonique. Semaine du 18 au 25 novembre. Exercice 5 : Utilisation de l'énergie. 1. On considère un système masse-ressort horizontal

LOSCILLATEUR HARMONIQUE

Il existe une manière très simple de visualiser un mouvement harmonique : il suffit d'accrocher une masse à l'extrémité d'un ressort et de la laisser osciller.

E R M eca(3) ? ER ? ´Oscillateur harmonique amorti

Le référentiel terrestre est supposé ga- liléen. Un point matériel M de masse m est lié. `a un ressort horizontal l'autre extrémité.

Oscillateur harmonique Oscillateur harmonique

13 nov. 2017 Exercice 3 : Oscillateur masse-ressort vertical. [??0] ... TD E3 : Oscillateur harmonique ... oscillations et comparer au cas horizontal.

Équilibre. Oscillateur harmonique.

Le premier exemple classique est celui d'un point matériel M accroché à l'extrémité d'un ressort enfilé sur une tige horizontale. Choisissons une base telle que

Physique MPSI-PCSI-PTSI - Cours complet et exercices corrigés

L’oscillateur harmonique étudié dans ce chapitre est un oscillateur méca-nique constitué d’un ressort et d’une masse Cet exemple simple permettra d’introduire le concept fondamental d’équation di?érentielle Plus générale-ment le modèle de l’oscillateur harmonique rend compte de l’évolution d’un système

Chapitre 12a – La dynamique du mouvement harmonique simple

qui contient un ressort dont la constante de rappel est connue se donnent une poussée se laissent osciller et mesurent la période naturelle d’oscillation Assise dans un dispositif dont la constante de rappel est de 500 N/m une astronaute prend 231 s pour effectuer une oscillation complète : on désire

Oscillateur harmonique horizontal (cours) LE DISPOSITIF

Oscillateur harmonique horizontal (cours) LE DISPOSITIF SOLIDE-RESSORT Source:http://pagesperso-orange fr/physique chimie Cette leçon comporte cinq paragraphes 1- FORCE DE RAPPEL EXERCEE PAR UN RESSORT Un ressort exerce sur un solide une force de rappel F proportionnelle à son allongement: L – L0: F = K ½L – L0½ (1)

Coursdemécanique - Physagreg

Nous étudierons dans ce chapitre en premier lieu l’oscillateur harmonique solide-ressort horizontalenousintroduironsdonclaforcederappelduressortetnousdécouvrironsl’équation di?érentielledel’oscillateurharmoniqueetsasolution

Searches related to oscillateur harmonique ressort horizontal PDF

de l’oscillateur harmonique NON amorti et libre (non excité) Cf Cours Cf Poly : dans le cas du pendule simple la modélisation de l’oscillateur harmonique est valable lorsque le portrait de phase est assimilable à une ellipse Ce qui est le cas pour les faibles amplitudes : ?m = ? ? 20

Comment choisir un oscillateur solide-ressort vertical ?

L’oscillateur solide-ressort vertical sera ensuite abordé : tout d’abord, ce sera l’occasion deretrouver l’équation di?érentielle de l’oscillateur harmonique, puis nous introduirons des frotte-ments ?uides pour voir le comportement du système. En?n, nous aborderons un oscillateurà deux dimensions, le pendule simple.

Comment calculer l’harmonique d’un oscillateur ?

Et finalement A = xm . Les oscillations du point M sont sinusoïdales d’amplitude xm et de période propre: L’oscillateur est qualifié d’harmonique car ses oscillations sont d’amplitude constante, et de période propre également constante dont la valeur ne dépend que des caractéristiques du système solide-ressort.

Quels sont les oscillateurs harmoniques de l’enfant ?

L’enfant oscille donc indéfiniment (pas de frottement) à la période: Le pendule simple est un oscillateur harmonique. On reprend l’exemple des oscillateurs précédents: système masse-ressort horizontal ou vertical, ou balançoire.

Qu'est-ce que l'oscillateur harmonique amorti?

? D´e?nition : On appelle Oscillateur Harmonique Amorti un syst`eme `a un degr´e de libert´e dont l’´evolution est r´egie par l’´equation di?´erentielle lin´eaire du second ordre : x¨ + x? ? +?2 0x = 0 (EOHA) avec ?0la pulsation propre et ? le temps de relaxation (encore appel´ee dur´ee caract´eristique).

ERM´eca(3)

?ER?´Oscillateur harmonique amorti Le r´ef´erentiel terrestre est suppos´e ga- lil´een.

Un point mat´erielMde massemest li´e

`a un ressort horizontal, l"autre extr´emit´e du ressort ´etant fixe enA.

Dans son domaine d"´elasticit´e, le ressort non tendu est caract´eris´e par une constante de raideur

ket une longueur `a videl0. Le pointMglisse le long de l"axe (Ox) `a partir de sa position d"´equilibre situ´ee enOet est

rep´er´e sur cet axe par son abscissex. Il existe entre le mobile et le support un frottement de type

visqueux. La force de frottement est de la forme :-→Fr=-hx-→ex, o`u la constantehest positive.

On posera :ω20=k

metω0Q=hm. L"oscillateur harmonique est caract´eris´e par le couple(Q,ω0). A l"instantt= 0, le mobile est abandonn´e sans vitesse initiale d"une positionx0(avecx0?= 0).

1)Faire le bilan des forces appliqu´ees au mobile lorsqu"il setrouve en un point d"abscissex

quelconque.´Etablir l"´equation diff´erentielle dontx(t) est solution. ´Ecrire l"´energie m´ecaniqueEmdeMen fonction dexet de x. Le syst`eme est-il conservatif?

Que vaut?dEm

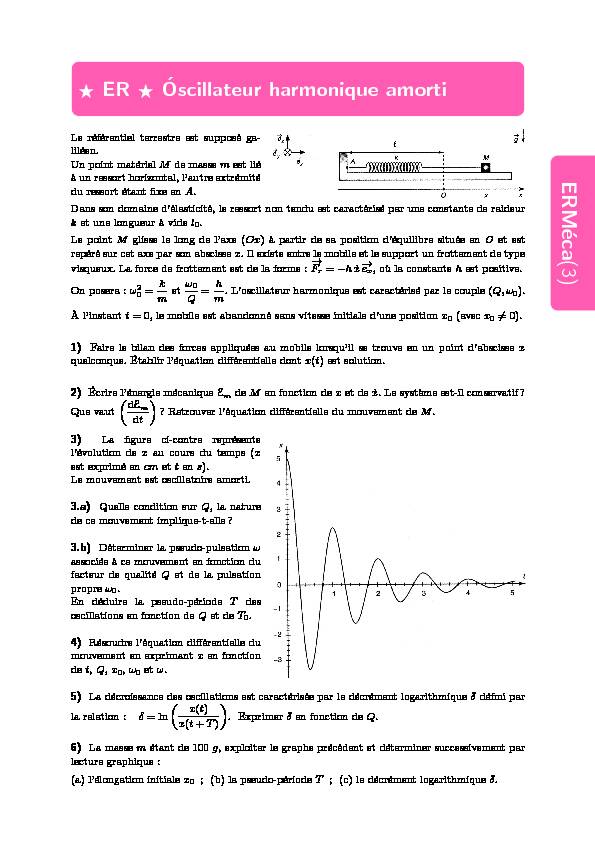
dt? ? Retrouver l"´equation diff´erentielle du mouvement deM.

3)La figure ci-contre repr´esente

l"´evolution dexau cours du temps (x est exprim´e encmettens).

Le mouvement est oscillatoire amorti.

3.a)Quelle condition surQ, la nature

de ce mouvement implique-t-elle?

3.b)D´eterminer la pseudo-pulsationω

associ´ee `a ce mouvement en fonction du facteur de qualit´eQet de la pulsation propreω0.

En d´eduire la pseudo-p´eriodeTdes

oscillations en fonction deQet deT0.

4)R´esoudre l"´equation diff´erentielle du

mouvement en exprimantxen fonction det,Q,x0,ω0etω.

5)La d´ecroissance des oscillations est caract´eris´ee par le d´ecr´ement logarithmiqueδd´efini par

la relation :δ= ln?x(t) x(t+T)? . Exprimerδen fonction deQ.

6)La massem´etant de 100g, exploiter le graphe pr´ec´edent et d´eterminer successivement par

lecture graphique :

(a) l"´elongation initialex0; (b) la pseudo-p´eriodeT; (c) le d´ecr´ement logarithmiqueδ.

ERM´eca(3)

?Oscillateur harmonique amortiPTSI-A|2011-2012

En d´eduire :

(d) le facteur de qualit´eQ; (e) la p´eriode propreT0; (f) le coefficient d"amortissementh; (g) la constante de raideurkdu ressort.

7)Le portrait de phase de l"oscilla-

teur harmonique amorti est repr´esent´e ci-contre dans le plan de phase (O, x,x).

D´eterminer successivement par lecture

graphique : (a) la nature du r´egime de l"oscillateur; (b) la vitesse initialev0; (c) l"´elongation initialex0; (d) l"´elongation finalexF; (e) le d´ecr´ement logarithmiqueδ.

Vos r´esultats sont-ils en accord avec

l"analyse effectu´ee en6)?

8)En se pla¸cant dans le cas d"un oscillateur tr`es peu amorti (Q?12), montrer que l"´energie

m´ecaniqueEm(t) du syst`eme v´erifie par approximation : m(t)-Em(t+T) Em(t)?2πQ(Rque : On rappelle que pourx?1 :ex?1 +x)

PTSI-A|2011-2012

ERM´eca(3)

Oscillateur harmonique amorti?

Solution

1)•Le point mat´erielMde massemest ´etudi´e dans le r´ef´eretiel terrestre suppos´e galil´een.

Soumis `a sonpoids, `a la r´eaction du support horizontal qui se d´ecompose en unecomposante

normale de la r´eaction-→RN=RN-→ezet une composante tangentielle qui constitue laforce de

frottements-→Fr=-hx-→ex, ainsi qu"`a laforce de rappel du ressort:-→T=-k(l-l0)-→ex=-kx-→ex.

•LeP.F.D.donne :m-→aM/RT=m-→g+-→RN+-→Fr+-→T •Comme-→aM/RT= ¨x-→ex, on en d´eduit, en projetant dans la base cart´esienne :?m¨x=-hx-kx

0 =-mg+RN

d"o`u : ¨x+h mx+kmx= 0?¨x+ω0Qx+ω20x= 0??.

2)•Em=Ek+Ep=1

2mx2+12kx2

dEm=δWNC=δW(-→RN)?

0 car-→RN?d--→OM+δW(-→Fr) =-→Fr·d--→OM=-hx2dt <0

→donc l"´energie m´ecanique diminue (Em?) au cours du temps (dt >0) →doncle syst`eme n"est pas conservatifet on a :dEm dt=-hx2<0

Soit :

dt?

12mx2+12kx2?

=mx¨x+kxx=-hx2Ce qui permet de retrouver??.

3.a) La solutionx(t)de??doit ˆetre pseudo-sinuso¨ıdale, donc de la forme

x(t) = (Acosωt+Bsinωt)exp(-αt) Pour cela, il faut que l"´equation caract´eristique de??(r2+ω0

Qr+ω20= 0) admette un discriminant

n´egatif :

Δ =ω20

Q2-4ω20<0, soitun facteur de qualit´eQ >12

3.b)Alors, l"´equation caract´eristique admet deux racines complexes :???????r

1=-ω0

2Q-j?

2=-ω02Q-jω0?1-14Q2=-α-jω

2=-ω0

2Q+j?

Soit un mouvement depseudo-pulsation :ω=ω0?

1-14Q2(??)

pseudo-p´eriode :T=T0

1-14Q2

avecω=2πTetω0=2πT0

4)Alors?x(t) = (Acosωt+Bsinωt)exp(-αt)

x(t) = ((Bω-Aα)cosωt-(Aω+Bα)sinωt)exp(-αt)

Or?x(t= 0) =x0=A

x(t= 0) = 0 =Bω-AαSoit :?A=x0

B=αx0

ω=ω0x02ωQ

D"o`u :x(t) =x0?

cosωt+ω0

2Qωsinωt?

exp? -ω0t2Q?

5)x(t) est tel quex(t+T) =x0?

cosωt+ω02Qωsinωt? exp? -ω0t2Q? exp? -ω0T2Q?

ERM´eca(3)

?Oscillateur harmonique amortiPTSI-A|2011-2012

Soit :x(t+T) =x(t)exp?

-ω0T2Q? d"o`u :δ≡lnx(t) x(t+T)= ln? exp? -ω0T2Q?? =ω0T2Q???????

δ=ω0T

2Q=2π?4Q2-1

6) Graphiquement :x0= 5cm T= 1s δ= lnx(0)x(T)≂=ln52,3= 0,78

D"apr`es5), on a :

Q=1

2?1 +4π2δ2≈4,08

D"apr`es (??), on a :

0=T?

1-14Q2≈992ms

20=k mk=mω20=m4π2T20≈4,01kg.s-2(ouN.m-1)avecm= 0,1kg.

7) d"apr`es le portrait de phase :

a) ce r´egime est pseudo-p´eriodique b)v0= x0= 0m.s-1 c)x0= 5cm d)xF= 0cm e)δ= lnx(0) x(T)≂=ln52,25≈0,80

δ= lnx(T)

x(2T)≂=ln2,251≈0,81

δ= lnx(T

x(3T2)≂=

R´esultats coh´erents avec la question6).

8)Em(t+T) =Ek(t+T) +Ep(t+T) =1

2mx2(t+T) +12kx2(t+T)

x(t+T) =x(t)exp(-αT) x(t+T) = x(t)exp(-αT)? →Em(t+T) =Em(t)exp(-2αT) =Em(t)exp? -ω0T avecT≈T0carQ?1

2, soitω0T≈2π, d"o`u :

m(t)-Em(t+T)

Em(t)= 1-exp?

-2πQ? ≈1-?

1-2πQ?

=2πQquotesdbs_dbs2.pdfusesText_4

[PDF] système squelettique fonction

[PDF] système osseux définition

[PDF] système squelettique humain

[PDF] programme sciences école primaire

[PDF] à la place de synonyme

[PDF] à la place en anglais

[PDF] "à la place de" "au lieu de"

[PDF] système verbal définition

[PDF] outils prevention tabac

[PDF] système verbal français

[PDF] projet bac sig

[PDF] place charles de gaulle marseille

[PDF] place charles de gaulle lyon

[PDF] place charles de gaulle paris

[PDF] place de l'étoile synonyme

[PDF] E R M eca(3) ? ER ? ´Oscillateur harmonique amorti

Comment choisir un oscillateur solide-ressort vertical ?

Comment calculer l’harmonique d’un oscillateur ?

Quels sont les oscillateurs harmoniques de l’enfant ?

Qu'est-ce que l'oscillateur harmonique amorti?

ERM´eca(3)

Un point mat´erielMde massemest li´e

On posera :ω20=k

1)Faire le bilan des forces appliqu´ees au mobile lorsqu"il setrouve en un point d"abscissex

Que vaut?dEm

3)La figure ci-contre repr´esente

Le mouvement est oscillatoire amorti.

3.a)Quelle condition surQ, la nature

3.b)D´eterminer la pseudo-pulsationω

En d´eduire la pseudo-p´eriodeTdes

4)R´esoudre l"´equation diff´erentielle du

5)La d´ecroissance des oscillations est caract´eris´ee par le d´ecr´ement logarithmiqueδd´efini par

6)La massem´etant de 100g, exploiter le graphe pr´ec´edent et d´eterminer successivement par

ERM´eca(3)

En d´eduire :

7)Le portrait de phase de l"oscilla-

D´eterminer successivement par lecture

Vos r´esultats sont-ils en accord avec

8)En se pla¸cant dans le cas d"un oscillateur tr`es peu amorti (Q?12), montrer que l"´energie

PTSI-A|2011-2012

ERM´eca(3)

Oscillateur harmonique amorti?

Solution

1)•Le point mat´erielMde massemest ´etudi´e dans le r´ef´eretiel terrestre suppos´e galil´een.

0 =-mg+RN

2)•Em=Ek+Ep=1

2mx2+12kx2

0 car-→RN?d--→OM+δW(-→Fr) =-→Fr·d--→OM=-hx2dt <0

Soit :

12mx2+12kx2?

3.a) La solutionx(t)de??doit ˆetre pseudo-sinuso¨ıdale, donc de la forme

Qr+ω20= 0) admette un discriminant

Δ =ω20

Q2-4ω20<0, soitun facteur de qualit´eQ >12

3.b)Alors, l"´equation caract´eristique admet deux racines complexes :???????r

1=-ω0

2=-ω02Q-jω0?1-14Q2=-α-jω

2=-ω0

Soit un mouvement depseudo-pulsation :ω=ω0?

1-14Q2(??)

1-14Q2

4)Alors?x(t) = (Acosωt+Bsinωt)exp(-αt)

Or?x(t= 0) =x0=A

B=αx0

ω=ω0x02ωQ

D"o`u :x(t) =x0?

2Qωsinωt?

5)x(t) est tel quex(t+T) =x0?

ERM´eca(3)

Soit :x(t+T) =x(t)exp?

δ=ω0T

2Q=2π?4Q2-1

6) Graphiquement :x0= 5cm T= 1s δ= lnx(0)x(T)≂=ln52,3= 0,78

D"apr`es5), on a :

2?1 +4π2δ2≈4,08

D"apr`es (??), on a :

1-14Q2≈992ms

7) d"apr`es le portrait de phase :

δ= lnx(T)

δ= lnx(T

R´esultats coh´erents avec la question6).

8)Em(t+T) =Ek(t+T) +Ep(t+T) =1

2mx2(t+T) +12kx2(t+T)

2, soitω0T≈2π, d"o`u :

Em(t)= 1-exp?

1-2πQ?