 Inverse Laplace Transform
Inverse Laplace Transform
Inverse Laplace Transform. In this lecture we look at the problem of finding inverse Laplace transforms. In other words given how do we find.
 Inverse Laplace Transforms: Expressions with Error Functions
Inverse Laplace Transforms: Expressions with Error Functions
Auxiliary Sections > Integral Transforms > Tables of Inverse Laplace Transforms > Inverse Laplace Inverse transform f(x) = 1. 2πi. ∫ c+i∞ c−i∞ epx ˜f(p) ...
 What are and what are not
What are and what are not
https://ul.qucosa.de/api/qucosa%3A31590/attachment/ATT-0/
 Inverse Laplace Transforms: Expressions with Exponential Functions
Inverse Laplace Transforms: Expressions with Exponential Functions
Auxiliary Sections > Integral Transforms > Tables of Inverse Laplace Transforms > Inverse Laplace Inverse transform f(x) = 1. 2πi. ∫ c+i∞ c−i∞ epx ˜f(p) ...
 Regularization of the Inverse Laplace Transform with Applications in
Regularization of the Inverse Laplace Transform with Applications in
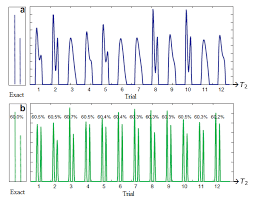
٠٦/١٢/٢٠١٦ Recover the distribution of amplitudes f(T2) present in the signal via an inverse Laplace transform (ILT). Christiana Sabett. ILT ...
 Inverse Laplace transforms via residue theory The Laplace
Inverse Laplace transforms via residue theory The Laplace
The in erse Laplace transform. The formula for the inverse Laplace transform was obtained in the previous section as: /(t) = 12πϳ/Х+ЦА. Е┴Х'ЦА. F(s)eЕtds. The
 The Inverse Laplace Transform and Analytic Pseudo-Differential
The Inverse Laplace Transform and Analytic Pseudo-Differential
Key Words: Laplace transform; inverse Laplace transform; pseudo-differential operators; differential operator of infinite order. 1. INTRODUCTION. w x. An
 Inverse Laplace Transform - EqWorld
Inverse Laplace Transform - EqWorld
Inverse Laplace Transforms: Expressions with Inverse. Trigonometric Functions. No. Laplace transform. ˜f(p). Inverse transform
 Inverse Laplace Transform - EqWorld
Inverse Laplace Transform - EqWorld
Polyanin A. D. and Manzhirov
 6.3 Inverse Laplace Transforms
6.3 Inverse Laplace Transforms
Example 6.24 illustrates that inverse Laplace transforms are not unique. However it can be shown that
 The Inverse Laplace Transform
The Inverse Laplace Transform
26. The Inverse Laplace Transform. We now know how to find Laplace transforms of “unknown” functions satisfying various initial- value problems.
 Lecture XV: Inverse Laplace transform
Lecture XV: Inverse Laplace transform
07-Nov-2008 Inverse Laplace transform of a rational function poles zeros
 Chapter 7. Laplace Transforms. Section 7.4 Inverse Laplace
Chapter 7. Laplace Transforms. Section 7.4 Inverse Laplace
Chapter 7. Laplace Transforms. Section 7.4 Inverse Laplace Transform. Definition 1. Given a function F(s) if there is a function f(t) that is continuous on.
 Lecture : 2 (INVERSE LAPLACE TRANSFORMS)
Lecture : 2 (INVERSE LAPLACE TRANSFORMS)
L is called the inverse Laplace transformation operator. 2.2 Inverse Laplace Transform of some elementary functions: S. No. )( sF. 1.
 Section 7.4: Inverse Laplace Transform A natural question to ask
Section 7.4: Inverse Laplace Transform A natural question to ask
This idea has more than theoretical interest however; we'll see in the next section that finding inverse Laplace transforms is a critical step in solving
 Inverse Laplace Transform - EqWorld
Inverse Laplace Transform - EqWorld
Polyanin A. D. and Manzhirov
 Lecture 10 Solution via Laplace transform and matrix exponential
Lecture 10 Solution via Laplace transform and matrix exponential
Laplace transform of matrix valued function suppose z : R+ ? R convention: upper case denotes Laplace transform ... take inverse transform.
 Inverse Laplace Transform Practice Problems (Answers on the last
Inverse Laplace Transform Practice Problems (Answers on the last
(A) Continuous Examples (no step functions): Compute the inverse Laplace transform of the given function. • The same table can be used to find the inverse
 The Inverse Laplace Transform 1. If L{f(t)} = F(s) then the inverse
The Inverse Laplace Transform 1. If L{f(t)} = F(s) then the inverse
for any constant c. 2. Example: The inverse Laplace transform of. U(s) = 1 s3. +. 6.
 [PDF] The Inverse Laplace Transform
[PDF] The Inverse Laplace Transform
26 The Inverse Laplace Transform We now know how to find Laplace transforms of “unknown” functions satisfying various initial- value problems
 [PDF] Lecture : 2 (INVERSE LAPLACE TRANSFORMS) - Hansraj College
[PDF] Lecture : 2 (INVERSE LAPLACE TRANSFORMS) - Hansraj College
L is called the inverse Laplace transformation operator 2 2 Inverse Laplace Transform of some elementary functions: S No )( sF 1
 [PDF] Math 3331 Differential Equations - 53 The Inverse Laplace Transform
[PDF] Math 3331 Differential Equations - 53 The Inverse Laplace Transform
Basic Definition In-Class Exercises Partial Fractions Examples Examples 5 3 The Inverse Laplace Compute the inverse Laplace transform of Y (s) = 1
 [PDF] Chapter 8 LAPLACE TRANSFORMS AND INVERSE LAPLACE
[PDF] Chapter 8 LAPLACE TRANSFORMS AND INVERSE LAPLACE
An inverse Laplace transform of F(s) designated by L-¹{F(s)} is an- other function f(x) having the property that L{f(x)} = F(s) The simplest technique for
 [PDF] laplace transform
[PDF] laplace transform
Mostly used to find haplace Inverse Transformation for Example= t Find haplace of sex sin (1-x)dx
 [PDF] Table of Laplace Transformspdf - Purdue Math
[PDF] Table of Laplace Transformspdf - Purdue Math
6 8 Laplace Transform: General Formulas Formula Name Comments Sec F(s) = L{f(t))} = 00 e-stf(t) dt Definition of Transform 6 1 Inverse Transform
 [PDF] Inverse Laplace Transform :
[PDF] Inverse Laplace Transform :
The Inverse Laplace's transform for function denoted by defined as; iff ( ) (1) That form Laplace transform into the original function Example 1:
 [PDF] Chapter 7 Laplace Transforms Section 74 Inverse - TAMU Math
[PDF] Chapter 7 Laplace Transforms Section 74 Inverse - TAMU Math
Laplace Transforms Section 7 4 Inverse Laplace Transform Definition 1 Given a function F(s) if there is a function f(
 [PDF] The Inverse Laplace Transform 1 If L{f(t)} = F(s) then the inverse
[PDF] The Inverse Laplace Transform 1 If L{f(t)} = F(s) then the inverse
for any constant c 2 Example: The inverse Laplace transform of U(s) = 1 s3 + 6
 [PDF] TRANSFORMS
[PDF] TRANSFORMS
Methods of finding inverse Laplace transforms Partial fractions method Series methods Method of differential equations Differentiation
What is the inverse Laplace transform?
A Laplace transform which is a constant multiplied by a function has an inverse of the constant multiplied by the inverse of the function. First shift theorem: L ? 1 { F ( s ? a ) } = e a t f ( t ) , where f(t) is the inverse transform of F(s).What is the inverse Laplace transform of 1 /( s 4?
It is equivalent to 1(4?1)Does inverse Laplace transform exist?
Does such an inverse integral transform exist for the Laplace transform? Yes, it does In this section we will derive the inverse Laplace transform integral and show how it is used. and the inverse Fourier transform, g(t)=f(t)e?ct=12?????ˆg(?)e?i?td?.- A good first step is usually to reduce the function to partial fractions. Now the inverse Laplace transform of 2 (s?1) is 2e1 t.
The Inverse Laplace Transform
We now know how to find Laplace transforms of unknown" functions satisfying various initial- value problems. Of course, it"s not the transforms of those unknown function which are usuallyof interest. It"s the functions, themselves, that are of interest. So let us turn to the general issue
of finding a functiony(t)when all we know is its Laplace transformY(s).26.1 Basic Notions
On Recovering a Function from Its Transform
In attempting to solve the differential equation in example25.1, we gotY(s)=4
s-3, which, sinceY(s)=L[y(t)]|sand4
s-3=L?4e3t???s, we rewrote as L [y(t)]=L?4e3t?.From this, seemed reasonable to conclude that
y(t)=4e3t. But, what if there were another functionf(t)with the same transform as 4e3t? Then we could not be sure whether the abovey(t)should be 4e3tor that other functionf(t). Fortunately, someone has managed to prove the following:Theorem 26.1 (uniqueness of the transforms)
Suppose
fandgare any two piecewise continuous functions on[0,∞)of exponential order and having the same Laplace transforms,L[f]=L[g].
Then, as piecewise continuous functions,
f(t)=g(t)on[0,∞). 527528The Inverse Laplace Transform
(You may want to quickly review the discussion of equality of piecewise continuous func- tions" on page 497.) This theorem actually follows from another result that willbe briefly discussed at the end of this section. What is important, now, is that this theoremassures us that, if L [y(t)]|s=L?4e3t???s, then y(t)=4e3t, at least fort≥0. What about fort<0? Well, keep in mind that the Laplace transform of any functionf,F(s)=L[f]|s=?
0 f(t)e-stdt, involves integration only over the positiveT-axis. The behavior offon the negativeT-axis has no effect on the formula forF(s). In fact,f(t)need not even be defined fort<0. So, even if theyexist, therecanbeno way torecoverthevaluesoff(t)onthenegativeT-axisfrom F(s). But that is not a real concern because we will just use the Laplace transform for problems over the positiveT-axis problems in which we have initialvalues att=0 and want to know what happenslater. What all this means is that we are only interested in functions oftwitht≥0. That was hinted at when we began our discussions of the Laplace transform (see note 3 on page 477), but we did not make an issue of it to avoid getting too distracted by technical details. Now, with the inverse transform, requiringt≥0 becomes more of an issue. Still, there is no need to obsess about this any more than necessary, or to suddenly start including fort≥0" with every formula oft. Let us just agree that the negativeT-axis is irrelevant to our discussions, and that in all formulas involvingt, it is assumed thatt≥0.Example 26.1:Somewhere above, we have
y(t)=4e3t.What we really mean is that
y(t)=4e3tfort≥0.Wehavenoideawhat
y(t)isfort<0. Wedon"tevenknowwhether,inwhateverapplication this may have arisen, it makes sense to talk about y(t)fort<0, nor do we care.1The Inverse Laplace Transform Defined
We can now officially define the inverse Laplace transform: Given a functionF(s), theinverse Laplace transform of F, denoted byL-1[F], is that functionfwhose Laplace transform isF.1For example: Whatify(t)denoted thetemperatureinacup of coffeetminutesafter beingpoured? Doesitmake
sense to consider the temperature of the coffee before it exists? (Answer this assuming you are not a Zen master.)
Basic Notions529
More succinctly:
f(t)=L-1[F(s)]|t??L[f(t)]|s=F(s). Our theoremonuniqueness(theorem26.1) (alongwithour understandingabout alwaysassum- ingt≥0") assures us that the above definition forL-1[F]is unambiguous. In this definition, of course, we assumeF(s)can be given asL[f(t)]for some functionf.Example 26.2:We have
L-1?4s-3?
?t=4e3t because4 s-3=L?4e3t???s.Likewise, since
L?t3???s=6s4,
we have t3=L-1?6s4? ?t.The fact that
f(t)=L-1[F(s)]|t??L[f(t)]|s=F(s) means that any table of Laplace transforms (such as table 24.1 on page 484) is also a table of inverse Laplace transforms. Instead of reading off theF(s)for eachf(t)found, read off the f(t)for eachF(s). As you may have already noticed, we take inverse transforms of functions ofsthat are denoted by upper case Roman letters" and obtain functions oftthat are denoted by the cor- responding lower case Roman letter". These notational conventions are consistent with the notational conventions laid down earlier for the Laplace transform. We should also note that the phrase inverse Laplace transform" can refer to either the 'inverse transformed function"for to the process of computingffromF. By the way, there is a formula for computing inverse Laplace transforms. If you must know, it is L -1[F(s)]|t=12πlimY→+∞?
Y -Yet(σ+iξ)F(σ+iξ)dξ. The integral here is over a line in the complex plane, andσis a suitably chosen positive value. In deriving this formula, you actually verify uniqueness theorem 26.1. Unfortunately, deriving and verifying this formula goes beyond our current abilities.2 Don"t pretend to understand this formula, and don"t try to use it until you"ve had a course in complex variables. Besides, it is not nearly as useful as a good table of transforms.2Two derivations can be found in third edition ofTransforms and Applications Handbook(Ed: A. Poularikas,
CRC Press). One, using Fourier transforms, is in section 2.4.6 of the chapter on Fourier transforms by Howell.
The other, using results from the theory of complex analyticfunctions, is in section 5.6 of the chapter on Laplace
transforms by Poularikas and Seely.530The Inverse Laplace Transform
26.2 Linearity and Using Partial Fractions
Linearity of the Inverse Transform
The fact that the inverse Laplace transform is linear follows immediately from the linearity of the Laplace transform. To see that, let us considerL-1[αF(s)+βG(s)]whereαandβare any two constants andFandGare any two functions for which inverse Laplace transforms exist. Following our conventions, we"ll denote those inverse transforms byfandg. That is, f(t)=L-1[F(s)]|tandg(t)=L-1[G(s)]|t. Remember, this is completely the same as stating that L [f(t)]|s=F(s)andL[g(t)]|s=G(s). Because we already know the Laplace transform is linear, we know L This, along the definition of the inverse transform and the above definitions offandg, yields L Redoing these little computations with as many functions and constants as desired then gives us the next theorem: Theorem 26.2 (linearity of the inverse Laplace transform) The inverse Laplace transform transform is linear. That is,L-1[c1F1(s)+c2F2(s)+ ··· +cnFn(s)]
=c1L-1[F1(s)]+c2L[F2(s)]+ ··· +cnL[Fn(s)] when eachckis a constant and eachFkis a function having an inverse Laplace transform. Let"s now use the linearity to compute a few inverse transforms.Example 26.3:Let"s find
L-1?1s2+9?
?t.We know (or found in table 24.1 on page 484) that
L-1?3s2+9?
?t=sin(3t), which is almost what we want. To use this in computing our desired inverse transform, we will combine linearity with one of mathematics" oldest tricks (multiplying by1with, in this
case,1=3/3):
L-1?1s2+9?
?t=L-1?13·3s2+9? ?t=13L-1?3s2+9? ?t=13sin(3t).Linearity and Using Partial Fractions531
The use of linearity along with 'multiplying by 1" will be used again and again. Get used to it. Example 26.4:Let"s find the inverse Laplace transform of 30s7+8s-4.
We know
L-1?6!s7?
?t=t6andL-1?1s-4? ?t=e4t. So,L-1?30s7+8s-4?
?t=30L-1?1s7? ?t+8L-1?1s-4? ?t =30L-1?16!·6!s7?
?t+8e4t 306!L-1?6!s7?
?t+8e4t=306·5·4·3·2t6+8e4t, which, after a little arithmetic, reduces toL-1?30s7+8s-4?
?t=124t6+8e4t.Partial Fractions
When using the Laplace transform with differential equations, we often get transforms that can be converted via 'partial fractions" to forms that are easily inverse transformed using the tables andlinearity,asabove. Thismeansthatthegeneralmethod(s)of partialfractionsareparticularly important. By now, you should well-acquainted with using partial fractions remember, the basic idea is that, if we have a fraction of two polynomials Q(s) P(s) andP(s)can be factored into two smaller polynomialsP(s)=P1(s)P2(s),
then two other polynomialsQ1(s)andQ2(s)can be found so that Q(s) Moreover, if (as will usually be the case for us) the degree ofQ(s)is less than the degree of P(s), then the degree of eachQk(s)will be less than the degree of the correspondingPk(s). You probably used partial fractions to compute some of the integrals in the earlier chapters of this text. We"ll go through a few examples to both refresh our memories of this technique, and to see how it naturally arises in using the Laplace transform to solve differential equations.532The Inverse Laplace Transform
!?Example 26.5:In exercise 25.1e on page 523, you found that the Laplace transform of the solution to y??+4y=20e4twithy(0)=3andy?(0)=12 isY(s)=3s2-28(s-4)?s2+4?.
The partial fraction expansion of this is
Y(s)=3s2-28(s-4)?s2+4?=As-4+Bs+Cs2+4
for some constantsA,BandC. There are many ways to find these constants. The basic method is to undo" the partial fraction expansion by getting a common denominator and adding up the fractions on the right:3s2-28
(s-4)?s2+4?=As-4+Bs+Cs2+4A?s2+4?
(s-4)?s2+4?+(s-4)(Bs+C)(s-4)?s2+4? (A+B)s2+(C-4B)s+4(A-C) (s-4)?s2+4?. Cutting out the middle and canceling out the common denominator leads to the equation which, in turn, means that our constants satisfy the three bythree system 3=A+B0=C-4B
-28=4A-4C This is relatively simple system. Solving it however you wish, you obtainA=1andB=2andC=8.
HenceY(s)=As-4+Bs+Cs2+4=1s-4+2s+8s2+4,
and y(t)=L-1[Y(s)]|t=L-1?1s-4+2s+8s2+4? ?t =L-1?1 s-4? ?t+2L-1?ss2+4? t+8L-1?1s2+4? ?t =e4t+2L-1?s s2+22? t+8·12L-1?2s2+22? ?t =e4t+2cos(2t)+4sin(2t)Linearity and Using Partial Fractions533
!?Example 26.6:In example 25.2 on page 511 we obtainedY(s)=16(s-2)(s2-7s+12)+6s-38s2-7s+12
and, equivalently,Y(s)=6s2-50s+92(s-2)?s2-7s+12?
as the Laplace transform of the solution to some initial-value problem. While we could find partialfractionexpansionsfor eachtermofthefirstexpressionabove, it willcertainlybemore convenient to simply find the single partial fraction expansion for the second expression for Y(s). But before attempting that, we should note that one factor in the denominator can be further factored, s2-7s+12=(s-3)(s-4), giving usY(s)=6s2-50s+92(s-2)(s-3)(s-4).
Now we can seek the partial fraction expansion of
Y(s):6s2-50s+92
(s-2)(s-3)(s-4)=As-2+Bs-3+Cs-4 =A(s-3)(s-4)+B(s-2)(s-4)+C(s-2)(s-3) (s-2)(s-3)(s-4). Cutting out the middle and canceling out the common denominator leaves6s2-50s+92
=A(s-3)(s-4)+B(s-2)(s-4)+C(s-2)(s-3) .(26.1) Rather than multiplying out the right side of this equation and setting up the system thatA, BandCmust satisfy for this equation to hold (as we did in the previous example), let"s find these constants after making clever choices for the value of sin this last equation.Letting
s=2in equation (26.1):6?22?-50·2+92
=A(2-3)(2-4)+B(2-2)(2-4)+C(2-2)(2-3) ?→16=2A+0B+0C??A=8Letting
s=3in equation (26.1):6?32?-50·3+92
=A(3-3)(3-4)+B(3-2)(3-4)+C(3-2)(3-3) ?→-4=0A-B+0C??B=4534The Inverse Laplace Transform
Lettings=4in equation (26.1):
6?42?-50·4+92
=A(4-3)(4-4)+B(4-2)(4-4)+C(4-2)(4-3) ?→-12=0A+0B+2C??C= -6Combining the above results, we have
Y(s)=6s2-50s+76(s-2)(s-3)(s-4)
A s-2+Bs-3+Cs-4=8s-2+4s-3-6s-4.Hence,
y(t)=L-1[Y(s)]|t=L-1?8s-2+4s-3-6s-4? ?t =8L-1?1 s-2? ?t+4L-1?1s-3? ?t-6L-1?1s-4? ?t =8e2t+4e3t-6e4t Do recallhow todeal withrepeatedfactorsin thedenominator. In particular,if your denom- inator has factors of the form (s+c)nor?s2+bs+c?n for some positive integernand constantsbandc, then the corresponding partial fraction expansions are A 1 (s+c)n+A2(s+c)n-1+A3(s+c)n-2+ ··· +Ans+c and A 1s+B1 ?s2+bs+c?n+A2s+B2?s2+bs+c?n-1+A3s+B3?s2+bs+c?n-2+ ··· +Ans+Bns2+bs+c, respectively.Example 26.7:The partial fraction expansion of
Y(s)=2s2(s-6)3
is of the formA (s-6)3+B(s-6)2+Cs-6.To find the constants
A,BandC, we proceed as in the previous examples:
2s2 (s-6)3=A(s-6)3+B(s-6)2+Cs-6 AA+B(s-6)+C(s-6)2
(s-6)3.Inverse Transforms of Shifted Functions535
So we must have
2s2=A+B(s-6)+C(s-6)2.
The value of
Acan be easily found by lettings=6in this equation, and the values ofB andCcan be found by lettings=6after taking derivatives of both sides of this equation. Or we can multiply out the right side and rewrite the left sidemore explicitly, obtaining2s2+0s+0=Cs2+(B-12C)s+(A-6B+36C).
This tells us that the constants can be obtained by solving the system C=2B-12C=0
A-6B+36C=0
In either case, you will discover that
A=72,B=24andC=2.
Thus,Y(s)=2s2(s-6)3
A (s-6)3+B(s-6)2+Cs-6 72(s-6)3+24(s-6)2+2s-6. In the next section, we will discuss an easy way to find the inverse transform of each of the terms in this partial fraction expansion.
26.3 Inverse Transforms of Shifted Functions
transform. Of particular value to us is the first shifting identity L ?eatf(t)???s=F(s-a) whereF=L[f(t)]andais any fixed real number. In terms of the inverse transform, this is Lquotesdbs_dbs13.pdfusesText_19[PDF] qqs
[PDF] niveau bright
[PDF] abréviation exemple
[PDF] test bright gratuit
[PDF] formule du demi-perimetre du rectangle
[PDF] mensuration homme musculation
[PDF] mesurer tour de cuisse homme
[PDF] orientation scolaire belgique
[PDF] conseiller d'orientation bruxelles
[PDF] vocabulaire géométrie collège
[PDF] test tricam
[PDF] exemple programme larp
[PDF] test paramétrique exercice corrigé
[PDF] test non paramétrique pdf
