 Inverse Laplace Transform
Inverse Laplace Transform
Inverse Laplace Transform. In this lecture we look at the problem of finding inverse Laplace transforms. In other words given how do we find.
 Inverse Laplace Transforms: Expressions with Error Functions
Inverse Laplace Transforms: Expressions with Error Functions
Auxiliary Sections > Integral Transforms > Tables of Inverse Laplace Transforms > Inverse Laplace Inverse transform f(x) = 1. 2πi. ∫ c+i∞ c−i∞ epx ˜f(p) ...
 What are and what are not
What are and what are not
https://ul.qucosa.de/api/qucosa%3A31590/attachment/ATT-0/
 Inverse Laplace Transforms: Expressions with Exponential Functions
Inverse Laplace Transforms: Expressions with Exponential Functions
Auxiliary Sections > Integral Transforms > Tables of Inverse Laplace Transforms > Inverse Laplace Inverse transform f(x) = 1. 2πi. ∫ c+i∞ c−i∞ epx ˜f(p) ...
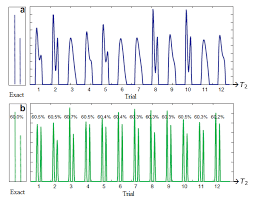 Regularization of the Inverse Laplace Transform with Applications in
Regularization of the Inverse Laplace Transform with Applications in
٠٦/١٢/٢٠١٦ Recover the distribution of amplitudes f(T2) present in the signal via an inverse Laplace transform (ILT). Christiana Sabett. ILT ...
 Inverse Laplace transforms via residue theory The Laplace
Inverse Laplace transforms via residue theory The Laplace
The in erse Laplace transform. The formula for the inverse Laplace transform was obtained in the previous section as: /(t) = 12πϳ/Х+ЦА. Е┴Х'ЦА. F(s)eЕtds. The
 The Inverse Laplace Transform and Analytic Pseudo-Differential
The Inverse Laplace Transform and Analytic Pseudo-Differential
Key Words: Laplace transform; inverse Laplace transform; pseudo-differential operators; differential operator of infinite order. 1. INTRODUCTION. w x. An
 The Inverse Laplace Transform
The Inverse Laplace Transform
We now know how to find Laplace transforms of “unknown” functions satisfying various initial- value problems. Of course it's not the transforms of those
 Inverse Laplace Transform - EqWorld
Inverse Laplace Transform - EqWorld
Inverse Laplace Transforms: Expressions with Inverse. Trigonometric Functions. No. Laplace transform. ˜f(p). Inverse transform
 Inverse Laplace Transform - EqWorld
Inverse Laplace Transform - EqWorld
Polyanin A. D. and Manzhirov
 6.3 Inverse Laplace Transforms
6.3 Inverse Laplace Transforms
Example 6.24 illustrates that inverse Laplace transforms are not unique. However it can be shown that
 The Inverse Laplace Transform
The Inverse Laplace Transform
26. The Inverse Laplace Transform. We now know how to find Laplace transforms of “unknown” functions satisfying various initial- value problems.
 Lecture XV: Inverse Laplace transform
Lecture XV: Inverse Laplace transform
07-Nov-2008 Inverse Laplace transform of a rational function poles zeros
 Chapter 7. Laplace Transforms. Section 7.4 Inverse Laplace
Chapter 7. Laplace Transforms. Section 7.4 Inverse Laplace
Chapter 7. Laplace Transforms. Section 7.4 Inverse Laplace Transform. Definition 1. Given a function F(s) if there is a function f(t) that is continuous on.
 Lecture : 2 (INVERSE LAPLACE TRANSFORMS)
Lecture : 2 (INVERSE LAPLACE TRANSFORMS)
L is called the inverse Laplace transformation operator. 2.2 Inverse Laplace Transform of some elementary functions: S. No. )( sF. 1.
 Section 7.4: Inverse Laplace Transform A natural question to ask
Section 7.4: Inverse Laplace Transform A natural question to ask
This idea has more than theoretical interest however; we'll see in the next section that finding inverse Laplace transforms is a critical step in solving
 Inverse Laplace Transform - EqWorld
Inverse Laplace Transform - EqWorld
Polyanin A. D. and Manzhirov
 Lecture 10 Solution via Laplace transform and matrix exponential
Lecture 10 Solution via Laplace transform and matrix exponential
Laplace transform of matrix valued function suppose z : R+ ? R convention: upper case denotes Laplace transform ... take inverse transform.
 Inverse Laplace Transform Practice Problems (Answers on the last
Inverse Laplace Transform Practice Problems (Answers on the last
(A) Continuous Examples (no step functions): Compute the inverse Laplace transform of the given function. • The same table can be used to find the inverse
 The Inverse Laplace Transform 1. If L{f(t)} = F(s) then the inverse
The Inverse Laplace Transform 1. If L{f(t)} = F(s) then the inverse
for any constant c. 2. Example: The inverse Laplace transform of. U(s) = 1 s3. +. 6.
 [PDF] The Inverse Laplace Transform
[PDF] The Inverse Laplace Transform
26 The Inverse Laplace Transform We now know how to find Laplace transforms of “unknown” functions satisfying various initial- value problems
 [PDF] Lecture : 2 (INVERSE LAPLACE TRANSFORMS) - Hansraj College
[PDF] Lecture : 2 (INVERSE LAPLACE TRANSFORMS) - Hansraj College
L is called the inverse Laplace transformation operator 2 2 Inverse Laplace Transform of some elementary functions: S No )( sF 1
 [PDF] Math 3331 Differential Equations - 53 The Inverse Laplace Transform
[PDF] Math 3331 Differential Equations - 53 The Inverse Laplace Transform
Basic Definition In-Class Exercises Partial Fractions Examples Examples 5 3 The Inverse Laplace Compute the inverse Laplace transform of Y (s) = 1
 [PDF] Chapter 8 LAPLACE TRANSFORMS AND INVERSE LAPLACE
[PDF] Chapter 8 LAPLACE TRANSFORMS AND INVERSE LAPLACE
An inverse Laplace transform of F(s) designated by L-¹{F(s)} is an- other function f(x) having the property that L{f(x)} = F(s) The simplest technique for
 [PDF] laplace transform
[PDF] laplace transform
Mostly used to find haplace Inverse Transformation for Example= t Find haplace of sex sin (1-x)dx
 [PDF] Table of Laplace Transformspdf - Purdue Math
[PDF] Table of Laplace Transformspdf - Purdue Math
6 8 Laplace Transform: General Formulas Formula Name Comments Sec F(s) = L{f(t))} = 00 e-stf(t) dt Definition of Transform 6 1 Inverse Transform
 [PDF] Inverse Laplace Transform :
[PDF] Inverse Laplace Transform :
The Inverse Laplace's transform for function denoted by defined as; iff ( ) (1) That form Laplace transform into the original function Example 1:
 [PDF] Chapter 7 Laplace Transforms Section 74 Inverse - TAMU Math
[PDF] Chapter 7 Laplace Transforms Section 74 Inverse - TAMU Math
Laplace Transforms Section 7 4 Inverse Laplace Transform Definition 1 Given a function F(s) if there is a function f(
 [PDF] The Inverse Laplace Transform 1 If L{f(t)} = F(s) then the inverse
[PDF] The Inverse Laplace Transform 1 If L{f(t)} = F(s) then the inverse
for any constant c 2 Example: The inverse Laplace transform of U(s) = 1 s3 + 6
 [PDF] TRANSFORMS
[PDF] TRANSFORMS
Methods of finding inverse Laplace transforms Partial fractions method Series methods Method of differential equations Differentiation
What is the inverse Laplace transform?
A Laplace transform which is a constant multiplied by a function has an inverse of the constant multiplied by the inverse of the function. First shift theorem: L ? 1 { F ( s ? a ) } = e a t f ( t ) , where f(t) is the inverse transform of F(s).What is the inverse Laplace transform of 1 /( s 4?
It is equivalent to 1(4?1)Does inverse Laplace transform exist?
Does such an inverse integral transform exist for the Laplace transform? Yes, it does In this section we will derive the inverse Laplace transform integral and show how it is used. and the inverse Fourier transform, g(t)=f(t)e?ct=12?????ˆg(?)e?i?td?.- A good first step is usually to reduce the function to partial fractions. Now the inverse Laplace transform of 2 (s?1) is 2e1 t.
LAPLACE
TRANSFORMS
MURRAY R. SPIEGEL, Ph. D.
Laplace transforms applications completely
explainedvWorks with all major texts
450 fully solved problems
Perfect for brushup
or exam prepUse with these courses:
Operational Calculus 9 Electrical Engineering
9 Mechanics
RT College Ikthematics
SCHAUM'S OUTLINE OF
THEORY AND PROBLEMS
OFLAPLACETRANSFORMS
MURRAY R. SPIEGEL, Ph.D.
Former Professor and Chairman.
Mathematics Department
Rensselaer Polytechnic Institute
Hartford Graduate Center
SCHAUM'S OUTLINE SERIES
McGRAW-HILL
New York
San FranciscoWashingtun. D.C. Auckland Rogoid Caracas LisbonLondon
MadridAlexien City,MilanAluntrcal New Delhi
San Juan
SingaporeSydneylbkva"lomnro
Copyright © 1965 by McGraw-Hill. Inc. All Rights Reserved. Printed in the United States of America. No part of this publication may be reproduced, stored in a retrieval -system, or transmitted, in any form or by any means, electronic, mechanical, photocopying, recording, or otherwise, without the prior written permission of the publisher. 6023112131415S11SH754321069
Preface
The theory of Laplace transforms or Laplace transformation, also referred to asoperational calculus, has in recent years become an essential part of the mathematicalbackground required of engineers, physicists, mathematicians and other scientists.Thisis because, in addition to being of great theoretical interest in itself, Laplace transformmethods provide easy and effective means for the solution of many problems arising invarious fields of science and engineering.
The subject originated in attempts to justify rigorously certain "operational rules"used by Heaviside in the latter part of the 19th century for solving equations in electro-
magnetic theory.These attempts finally proved successful in the early part of the 20thcentury through the efforts of Bromwich, Carson, van der Pol and other mathematicianswho employed complex variable theory.
This book is designed for use as a supplement to all current standard texts or as atextbook for a formal course in Laplace transform theory and applications.It should alsobe of considerable value to those taking courses in mathematics, physics, electrical engi-neering, mechanics, heat flow or any of the numerous other fields in which Laplacetransform methods are employed.
Each chapter begins with a clear statement of pertinent definitions, principles andtheorems together with illustrative and other descriptive material.This is followed by
graded sets of solved and supplementary problems. The solved problems serve to illustrateand amplify the theory, bring into sharp focus those fine points without which the studentcontinually feels himself on unsafe ground, and provide the repetition of basic principlesso vital to effective learning.Numerous proofs of theorems and derivations of formulasare included among the solved problems.The large number of supplementary problemswith answers serve as a complete review of the material in each chapter.
Topics covered include the properties of Laplace transforms and inverse Laplacetransforms together with applications to ordinary and partial differential equations, integralequations, difference equations and boundary-value problems.The theory using complexvariables is not treated until the last half of the book.This is done, first, so that thestudent may comprehend and appreciate more fully the theory, and the power, of thecomplex inversion formula and, second, to meet the needs of those who wish only anintroduction to the subject.Chapters on complex variable theory and Fourier series andintegrals, which are important in a discussion of the complex inversion formula, havebeen included for the benefit of those unfamiliar with these topics.
Considerably more material has been included here than can be covered in most firstcourses.This has been done to make the book more flexible, to provide a more usefulbook of reference and to stimulate further interest in the topics.
I wish to take this opportunity to thank the staff of the Schaum Publishing Companyfor their splendid cooperation.
M. R. SPIEGEL
Rensselaer Polytechnic Institute
January, 1965
CONTENTS
PageChapter
THE LAPLACE TRANSFORM................................1Definition of the Laplace transform. Notation. Laplace transforms of someelementary functions.Sectional or piecewise continuity.Functions of ex-ponential order.Sufficient conditions for existence of Laplace transforms.Some important properties of Laplace transforms. Linearity property. Firsttranslation or shifting property.Second translation or shifting property.Change of scale property. Laplace transform of derivatives.Laplace trans-form of integrals.Multiplication by tn.Division by t.Periodic functions.Behavior o (s)as s--.Initial-value theorem.Final-value theorem.Generalization of initial-value theorem. Generalization of final-value theorem.Methods of finding Laplace transforms.Direct method.Series method.
Method of differential equations.Differentiation with respect to a parameter.Miscellaneous methods. Use of Tables. Evaluation of integrals. Some special
functions.The gamma function.Bessel functions.The error function.The complementary error function.Sine and cosine integrals.Exponentialintegral.Unit step function.Unit impulse or Dirac delta function.Null
functions.Laplace transforms of special functions.1Chapter
2Chapter
3THE INVERSE LAPLACE TRANSFORM ....................
42Definition of inverse Laplace transform. Uniqueness of inverse Laplace trans-
forms.Lerch's theorem. Some inverse Laplace transforms. Some importantproperties of inverse Laplace transforms.Linearity property.First transla-tion or shifting property.Second translation or shifting property.Changeof scale property.Inverse Laplace transform of derivatives.Inverse Laplacetransform of integrals.Multiplication by sn.Division by s.The convolutionproperty.Methods of finding inverse Laplace transforms.Partial fractions
method.Series methods.Method of differential equations.Differentiationwith respect to a parameter.Miscellaneous methods.Use of Tables.Thecomplex inversion formula.The Heaviside expansion formula.The betafunction.Evaluation of integrals.
APPLICATIONS TO DIFFERENTIAL EQUATIONS..........
78Ordinary differential equations with constant coefficients.Ordinary differen-tial equations with variable coefficients.Simultaneous ordinary differentialequations.Applications to mechanics.Applications to electrical circuits.Applications to beams. Partial differential equations.
Chapter
4APPLICATIONS TO INTEGRAL ANDDIFFERENCE EQUATIONS..................................
Integral equations.Integral equations of convolution type.Abel's integralequation. The tautochrone problem. Integro-differential equations. Differenceequations.Differential-difference equations.
Chapter
5COMPLEX VARIABLE THEORY.............................
The complex number system.Polar form of complex numbers.Operations inpolar form. De Moivre's theorem.Roots of complex numbers.Functions.Limits and continuity.
Derivatives.Cauchy-Riemann equations.Line in-tegrals. Green's theorem in the plane. Integrals. Cauchy's theorem. Cauchy'sintegral formulas. Taylor's series. Singular points.
Poles.Laurent's series.
Residues.
Residue theorem.Evaluation of definite integrals.112 136CONTENTS
Chapter
6FOURIER SERIES AND INTEGRALS........................Fourier series. Odd and even functions. Half range Fourier sine and cosineseries. Complex form of Fourier series. Parseval's identity for Fourier series.Finite Fourier transforms. The Fourier integral. Complex form of Fourierintegrals.Fourier transforms.Fourier sine and cosine transforms.Theconvolution theorem. Parseval's identity for Fourier integrals.Relationshipof Fourier and Laplace transforms.Page
173Chapter
7THE COMPLEX INVERSION FORMULA...................201The complex inversion formula.The Bromwich contour.Use of residuetheorem in finding inverse Laplace transforms. A sufficient condition forthe integral around r to approach zero.Modification of Bromwich contourin case of branch points. Case of infinitely many singularities.
Chapter
8APPLICATIONS TO BOUNDARY-VALUE PROBLEMS.......219Boundary-value problems involving partial differential equations. Some im-portant partial differential equations. One dimensional heat conduction equa-tion.One dimensional wave equation.Longitudinal vibrations of a beam.Transverse vibrations of a beam. Heat conduction in a cylinder. Transmissionlines.Two and three dimensional problems.Solution of boundary-valueproblems by Laplace transforms.
APPENDIX A. TABLE OF GENERAL PROPERTIES OF
LAPLACE TRANSFORMS.................................243 APPENDIX B. TABLE OF SPECIAL LAPLACE TRANSFORMS.......... 245APPENDIX C. TABLE OF SPECIAL FUNCTIONS
.......................255Chapter 1
The Laplace Transform
DEFINITION OF THE LAPLACE TRANSFORM
Let F(t) be a function of t specified for t> 0.
Then the Laplace transform of F(t),
denoted by 4 (F(t)), is defined by {F(t))=f(s)=f e-StF(t) dt(1) 0where we assume at present that'the parameter s is real.Later it will be found usefulto consider s complex.
The Laplace transform of F(t) is said to exist if the integral (1) converges for somevalue of s; otherwise it does not exist.For sufficient conditions under which the Laplacetransform does exist, see Page 2.
NOTATION
If a function of t. is indicated in terms of a capital letter, such as F(t), G(t), Y(t), etc.,the Laplace transform of the function is denoted by the corresponding lower case letter,
i.e. f (s), g(s), y(s), etc.In other cases, a tilde (-) can be used to denote the Laplace trans-form. Thus, for example, the Laplace transform of u(t) is is (s).
LAPLACE TRANSFORMS OF SOME ELEMENTARY FUNCTIONS
The adjacent table shows
Laplace transforms of variouselementary functions.For de-tails of evaluation using defini-tion (1), see Problems-1 and 2.For a more extensive table seeAppendix B, Pages 245 to 254.F(t)
-C {F(t)} = f(8) 1.118>0s
2.ts2s>0
3.to!8 > 0sn
n = 0, 1, 2, ... Note.Factorial n = n! = 12 nAlso, by definition 0! = 1.4.eat1s > as-a
5. sin ata> 0s_82+a2 6. cos at88 > 082a2 7. sinh ata8 > jai82 - a2 8. cosh at8 > lat82a2 1 2THE LAPLACE TRANSFORM[CHAP. 1
SECTIONAL OR PIECEWISE CONTINUITY
A function is called sectionally continuous or piecewise continuous in an intervalc< t-< a if the interval can be subdivided into a finite number of intervals in each ofwhich the function is continuous and has finite right and left hand limits.
F(t) I/ j i tatit21t3RFig. 1-1
An example of a function which is sectionally continuous is shown graphically inFig. 1-1 above.This function has discontinuities at ti, t2 and t3.Note that the right andleft hand limits at t2, for example, are represented bylim F(t2 + E) = F(t2 + 0) = F(t2+)
e0andlim F(t2 - E) = F(t2- 0) = F(t2-)respectively, where cis positive.E-+0
FUNCTIONS OF EXPONENTIAL ORDER
If real constants M > 0 and y exist such that for all t > NI e-It F(t) I
< MorI F(t) 1< Melt we say that F(t) is a function of exponential order y as t- - or, briefly, is of exponential order. Example 1.F(t) = t2is of exponential order 3 (for example), since;t2j = t2 < eat for all t > 0.Example 2.
F(t) =et3is not of exponential order sinceIe-vt et' 1 =et3-yt can be made larger thanany given constant by increasing t.
Intuitively, functions of exponential order cannot "grow" in absolute value more rapidlythan Me"' as t increases.In practice, however, this is no restriction since M and y can beas large as desired.
Bounded functions, such as sin at or cos at, are of exponential order. SUFFICIENT CONDITIONS FOR EXISTENCE OF LAPLACE TRANSFORMSTheorem 1-1.
If F(t) is sectionally continuous in every finite interval 0 < t< N andof exponential order y for t > N, then its Laplace transform f (s) exists for all s > y.
For a proof of this see Problem 47.It must be emphasized that the stated conditionsare sufficient to guarantee the existence of the Laplace transform.If the conditions arenot satisfied, however, the Laplace transform may or may not exist [see Problem 32].Thus the conditions are not necessary for the existence of the Laplace transform.
For other sufficient conditions, see Problem 145.
CHAP. 11
THE LAPLACE TRANSFORM3
SOME IMPORTANT PROPERTIES OF LAPLACE TRANSFORMS
In the following list of theorems we assume, unless otherwise stated, that all functions satisfy the conditions of Theorem 1-1 so that their Laplace transforms exist. 1.Linearity property.
Theorem 1-2.
If c1 and C2 are any constants while F1(t) and F2(t) are functions with Laplace transforms f i (s) and f2 (s) respectively, then .({C1F1(t)+C2F2(t)I=C14 {Fi(t)} + c2a({F2(t)}=clfl(s) + C2f2(s)(2) The result is easily extended to more than two functions. Example.C (4t2 - 3 cos 2t + 5e-1}=4.C {t2} - 3.C {cos 2t} + 5.4 {e-t}4(83) --3(s2+4)+5Cs+1)
83s+5s3_ s2+4s+1 The symbol C, which transforms F(t) into f (s), is often called the Laplace trans-
formation operator.Because of the property of t expressed in this theorem, we saythat e( is a linear operator or that it has the linearity property.
2.First translation or shifting property.
Theorem 1-3.
IfaC {F(t)} = f(s)then
a( {eal F(t)}=f(s - a)(3)Example.Sincee {cos 2t} =S
.32+ 4 ,we have .C{e-tcos2t} = s+1=s+1(s+1)2+4s2+2s+5 3.Second translation or shifting property.
Theorem 1-4.
If(F(t))sandG(t) = td(t - a)t .({G(t))=e-as f(s)(4) Example.Sincei {t3} =s4= s4 ,the Laplace transform of the function G(t) =j(t - 2)3 t>2 10t<2 is 6e-2s/g4 4.Change of scale property.
Theorem 1-5.
If.( {F(t)} = f(s),then
.t {F(at)} Example.
Since.( {sin t} =s2 + 1we have(5)
{sin 3t} = 1 1_3 3 (s/3)2 + 1
s2 + 9 4THE LAPLACE TRANSFORM
5.Laplace transform of derivatives.
Theorem 1-6.
Ift {F(t)} = f(s),then
i (F'(t)) =s f(s) - F(O)[CHAP. 1 (6) if F(t) is continuous for 0 < t < N and of exponential order for t > N while F'(t) issectionally continuous for 0 < t < N.
Example.
If F(t) = cos 3t, thenr {F(t)} =82 + 9and we have
{F'(t)} {-3 sin 3t}=s (82+9 )- 182+ `9 The method is useful in finding Laplace
transforms without integration [see Problem 151.
Theorem 1-7.If in Theorem 1-6,F(t)fails to be continuous att = 0 butlim F(t) = F(0+)exists [but is not equal to F(0), which may or may not exist], thent-.o
.C {F'(t)) =sf(s) - F(0+)(7) Theorem 1-8.
If in Theorem 1-6, F(t) fails to be continuous at t = a, then J (F'(t))
=s f (s) - F(O) - e -°s { F(a+) - F(a-) }(8) where F(a+) - F(a-) is sometimes called the jump at the discontinuity t = a.For more than one discontinuity, appropriate modifications can be made. Theorem 1-9.
If{F(t) } = f (s),then
{F"(t)} =s2 f(s) - sF(0) - F'(0)(9) if F(t) and F'(t) are continuous for 0 = t < N and of exponential order for t > N while F"(t) is sectionally continuous for 0 t-:5 N. If. F(t) and F'(t) have discontinuities, appropriate modification of (9) can be made as in Theorems 1-7 and 1-8. Theorem 1-10.
If(' {F(t)} = f(s),then
4 (Fcn)(t) }
=sn f(s) -sn-' F(0) - sn2 F'(0) -sFcn-2,(0)- Fcn 1)(0)(10) if F(t), F'(t),...,F`n-"(t) are continuous for 0tN and of exponential order for t > N while F(n)(t) is sectionally continuous for 0 < t < N. 6. Laplace transform of integrals.
Theorem 1-11.
IfC {F(t)} = f(s),then
of if foF(u)du1 Example.Since t {sin 2t} =-+4 ,we have
J sin 2u du-2(J r 1US(82+4)
as can be verified directly. CHAP. 1)
THE LAPLACE TRANSFORM5
7.Multiplication by tn.
Theorem 1-12.
If.{F(t)} = f(s),then
-(' {tn F(t)} _(-1)n dsnf(s) Example.SinceC {e2t}=_1_s - 2 'we have
.e {te2t} .e {t2e2t}= (-1)n f(n)(s) d111 ds(s-2(s-2)2d( 1) _22d82 s-2(s-2) 8. Division by t.
Theorem 1-13.
If.{F(t)} = f(s),then
provided lim F(t)/t exists. t-.of f (u) du(13) s Exam le.
Since1sin tp({sin t} -82 + 1and Eo= 1,we havet
sin t l __f xdu t jJu2 + 1-tan' 1(11s) 9.Periodic functions.
Theorem 1-14.
Let F(t) have period T > 0 so that F(t + T) = F(t) [see Fig. 1-2]. Then F(t)T f° e-" F(t) dt {F'(t)}_(14)1 - e-ST Fig. 1-2
10.Behavior o (s) as s -* co.
Theorem 1-15.
Ife (F(t)} = f(s),then
lim f (s)=0 S -. 'Jo
11. Initial-value theorem.
Theorem 1-16.
If the indicated limits exist, then
lim F(t) =lim s f (s)t--0s-(15) (16) 6THE LAPLACE TRANSFORM
12. Final-value theorem.
Theorem 1-17.
If the indicated limits exist, then
lim F(t)=lim s f (s)t-. os-.o[CHAP. 1 (17) 13. Generalization of initial-value theorem.
If urn F(t)/G(t) = 1,
then we say that for values of t near t = 0 [small t], F(t) ist-.oclose to G(t) and we write F(t) - G(t) as t- 0.
Similarly if
lim f(s)/g(s) = 1,then we say that for large values of s, f (s) is -4 00close to g(s) and we write f (s) - g(s) as s With this notation we have the following generalization of Theorem 1-16. Theorem 1-18.
If F(t) - G(t) as t - 0, then f(s) - g(s) as s -> oo where f (s).C (F(t)) and g(s) _ .( {G(t)}. 14. Generalization of final-value theorem.
If lim F(t)/G(t) = 1, we write F(t) - G(t) as t
Similarly if lim f(s)/g(s) = 1,tWSowe write f (s) -- g(s) as s - 0.Then we have the following generalization of Theorem
1-17. _ Theorem 1-19.If F(t) ~ G(t) as t - oc, the (s) - g(s) as s - 0 where f (s) .C {F(t)} andg(s) _ .({G(t)}. METHODS OF FINDING LAPLACE TRANSFORMS
Various means are available for determining Laplace transforms as indicated in the following list. 1.Direct method.This involves direct use of definition (1).
2. Series method.If F(t) has a power series expansion given by F(t) =ao + ait + a2t2 +=I ante(18)n-o its Laplace transform can be obtained by taking the sum of the Laplace transforms of each term in the series. Thus ao a,2!-a2n! an.C {F(t)}=+++_(19)SS-s'3n-U$n+1 A condition under which the result is valid is that the series (19) be convergent for s > y. See Problems 34, 36, 39 and 48.
3. Method of differential equations.This involves finding a differential equation satis- fied by F(t) and then using the above theorems.See Problems 34 and 48. 4. Differentiation with respect to a parameter.See Problem 20. 5. Miscellaneous methods involving special devices such as indicated in the above theo- rems, for example Theorem 1-13. 6.Use of Tables (see Appendix).
CHAP. 1]
THE LAPLACE TRANSFORM
EVALUATION OF INTEGRALS
Iff (s) = C {F(t) },then
Taking the limit as s -> 0, we have7
f0 e-StF(t) dt=f(s)(20)f F(t) dt=f(0)(21)
0assuming the integral to be convergent.
The results (20) and (21) are often useful in evaluating various integrals. See Problems
45 and 46.
SOME SPECIAL FUNCTIONS
1. The Gamma function.
I > 0, we define the gamma function by
r(n) =fun- ' e-u du(22) 0 The following are some important properties of the gamma function. 1. r(n + 1)=n r(n),n > 0 Thus since r(1)1, we have I'(2) = 1, r(3) = 2 ! = 2, or(4) = 3! and in general r(n + 1) = n!,i is a positive integer.For this reason the function is some- times called the factorial function. 2. r(:)= N5 3. 4.For large n,r(n+1)-27rnn11 e-n
[Here - means "approximately equal to for large n". More exactly, we writeF(n) ~ G(n) iflim F(n)/G(n) = 1.]This is called Stirling's formula.
n < 0 we can define r(n) by r(n) =r(n + 1) n II. Bessel functions.
We define a Bessel function of order n by
_t2(t)=2nr(n+1)12(2n+2) Some important properties are0
_ ...(23)2.4(2n + 2)(2n + 4) 1. J-n (t)(-1)n Jn (t)i is a positive integer
2. Jn+Z (t) =2tJ, (t) -(t)
3. dtto Jn-i (t).I = 0, we haveJo(t) = -J1(t). 4.e 'h"-1/u) =1'Jn(t)unr(p) r(1- p)
-sin per '0 < p < 1 9!=-a This is called the generating function for the Bessel functions. 8THE. LAPLACE TRANSFORM
5.J. (t) satisfies Bessel's differential . equation.
t2 Y11(t) + t Y'(t) + (t2 - n2) Y(t) _ It is convenient to define
J0(it) = i-nIn(t) where I0(t)Bessel function of order n. III. The Error function is defined as
erf (t) =2e-u2 du 0 IV. The Complementary Error function is defined as erfc (t) =1erf (t).1 -2fte-u2du 0 V. The Sine and Cosine integrals are defined by
t Si (t)= fsin udu
0u Ci (t)
VI. The Exponential integral is defined asf
Cos udutu
00 eudu5Ei (t)=(26) (27) (28) VII.The Unit Step function, also called Heaviside's unit function, is defined as 'U(t - a) _{0t < a(29) See Fig. 1-3.1t > a
u(t - a) i a t0 [CHAP. 1 is called the modified (24) 5e_u2du
(25) I 1/E Fig. 1-3
Fig. 1-4
VIII.The Unit Impulse function or Dirac delta function... Consider the function
FE (t)
quotesdbs_dbs13.pdfusesText_19
4.Change of scale property.
Theorem 1-5.
If.( {F(t)} = f(s),then
.t {F(at)}Example.
Since.( {sin t} =s2 + 1we have(5)
{sin 3t} = 1 1_33 (s/3)2 + 1
s2 + 94THE LAPLACE TRANSFORM
5.Laplace transform of derivatives.
Theorem 1-6.
Ift {F(t)} = f(s),then
i (F'(t)) =s f(s) - F(O)[CHAP. 1 (6)if F(t) is continuous for 0 < t < N and of exponential order for t > N while F'(t) issectionally continuous for 0 < t < N.
Example.
If F(t) = cos 3t, thenr {F(t)} =82 + 9and we have
{F'(t)} {-3 sin 3t}=s (82+9 )- 182+ `9The method is useful in finding Laplace
transforms without integration [seeProblem 151.
Theorem 1-7.If in Theorem 1-6,F(t)fails to be continuous att = 0 butlim F(t) = F(0+)exists [but is not equal to F(0), which may or may not exist], thent-.o
.C {F'(t)) =sf(s) - F(0+)(7)Theorem 1-8.
If in Theorem 1-6, F(t) fails to be continuous at t = a, thenJ (F'(t))
=s f (s) - F(O) - e -°s { F(a+) - F(a-) }(8) where F(a+) - F(a-) is sometimes called the jump at the discontinuity t = a.For more than one discontinuity, appropriate modifications can be made.Theorem 1-9.
If{F(t) } = f (s),then
{F"(t)} =s2 f(s) - sF(0) - F'(0)(9) if F(t) and F'(t) are continuous for 0 = t < N and of exponential order for t > N while F"(t) is sectionally continuous for 0 t-:5 N. If. F(t) and F'(t) have discontinuities, appropriate modification of (9) can be made as in Theorems 1-7 and 1-8.Theorem 1-10.
If(' {F(t)} = f(s),then
4 (Fcn)(t) }
=sn f(s) -sn-' F(0) - sn2 F'(0) -sFcn-2,(0)- Fcn 1)(0)(10) if F(t), F'(t),...,F`n-"(t) are continuous for 0tN and of exponential order for t > N while F(n)(t) is sectionally continuous for 0 < t < N. 6.Laplace transform of integrals.
Theorem 1-11.
IfC {F(t)} = f(s),then
of if foF(u)du1Example.Since t {sin 2t} =-+4 ,we have
J sin 2u du-2(J r1US(82+4)
as can be verified directly.CHAP. 1)
THE LAPLACE TRANSFORM5
7.Multiplication by tn.
Theorem 1-12.
If.{F(t)} = f(s),then
-(' {tn F(t)} _(-1)n dsnf(s)Example.SinceC {e2t}=_1_s - 2 'we have
.e {te2t} .e {t2e2t}= (-1)n f(n)(s) d111 ds(s-2(s-2)2d( 1) _22d82 s-2(s-2) 8.Division by t.
Theorem 1-13.
If.{F(t)} = f(s),then
provided lim F(t)/t exists. t-.of f (u) du(13) sExam le.
Since1sin tp({sin t} -82 + 1and Eo= 1,we havet
sin t l __f xdu t jJu2 + 1-tan' 1(11s)9.Periodic functions.
Theorem 1-14.
Let F(t) have period T > 0 so that F(t + T) = F(t) [see Fig. 1-2]. Then F(t)T f° e-" F(t) dt {F'(t)}_(14)1 - e-STFig. 1-2
10.Behavior o (s) as s -* co.
Theorem 1-15.
Ife (F(t)} = f(s),then
lim f (s)=0S -. 'Jo
11.Initial-value theorem.
Theorem 1-16.
If the indicated limits exist, then
lim F(t) =lim s f (s)t--0s-(15) (16)6THE LAPLACE TRANSFORM
12.Final-value theorem.
Theorem 1-17.
If the indicated limits exist, then
lim F(t)=lim s f (s)t-. os-.o[CHAP. 1 (17) 13.Generalization of initial-value theorem.
If urn F(t)/G(t) = 1,
then we say that for values of t near t = 0 [small t], F(t) ist-.oclose to G(t) and we write F(t) - G(t) as t- 0.
Similarly if
lim f(s)/g(s) = 1,then we say that for large values of s, f (s) is -4 00close to g(s) and we write f (s) - g(s) as s With this notation we have the following generalization of Theorem 1-16.Theorem 1-18.
If F(t) - G(t) as t - 0, then f(s) - g(s) as s -> oo where f (s).C (F(t)) and g(s) _ .( {G(t)}. 14.Generalization of final-value theorem.
If lim F(t)/G(t) = 1, we write F(t) - G(t) as t
Similarly if lim f(s)/g(s) = 1,tWSowe write f (s) -- g(s) as s - 0.Then we have the following generalization of Theorem
1-17. _ Theorem 1-19.If F(t) ~ G(t) as t - oc, the (s) - g(s) as s - 0 where f (s) .C {F(t)} andg(s) _ .({G(t)}.METHODS OF FINDING LAPLACE TRANSFORMS
Various means are available for determining Laplace transforms as indicated in the following list.1.Direct method.This involves direct use of definition (1).
2. Series method.If F(t) has a power series expansion given by F(t) =ao + ait + a2t2 +=I ante(18)n-o its Laplace transform can be obtained by taking the sum of the Laplace transforms of each term in the series. Thus ao a,2!-a2n! an.C {F(t)}=+++_(19)SS-s'3n-U$n+1 A condition under which the result is valid is that the series (19) be convergent for s > y.See Problems 34, 36, 39 and 48.
3. Method of differential equations.This involves finding a differential equation satis- fied by F(t) and then using the above theorems.See Problems 34 and 48. 4. Differentiation with respect to a parameter.See Problem 20. 5. Miscellaneous methods involving special devices such as indicated in the above theo- rems, for example Theorem 1-13.6.Use of Tables (see Appendix).
CHAP. 1]
THE LAPLACE TRANSFORM
EVALUATION OF INTEGRALS
Iff (s) = C {F(t) },then
Taking the limit as s -> 0, we have7
f0 e-StF(t) dt=f(s)(20)fF(t) dt=f(0)(21)
0assuming the integral to be convergent.
The results (20) and (21) are often useful in evaluating various integrals.See Problems
45 and 46.
SOME SPECIAL FUNCTIONS
1.The Gamma function.
I > 0, we define the gamma function by
r(n) =fun- ' e-u du(22) 0 The following are some important properties of the gamma function. 1. r(n + 1)=n r(n),n > 0 Thus since r(1)1, we have I'(2) = 1, r(3) = 2 ! = 2, or(4) = 3! and in general r(n + 1) = n!,i is a positive integer.For this reason the function is some- times called the factorial function. 2. r(:)= N5 3.4.For large n,r(n+1)-27rnn11 e-n
[Here - means "approximately equal to for large n". More exactly, we writeF(n) ~ G(n) iflim F(n)/G(n) = 1.]This is called Stirling's formula.
n < 0 we can define r(n) by r(n) =r(n + 1) n II.Bessel functions.
We define a Bessel function of order n by
_t2(t)=2nr(n+1)12(2n+2)Some important properties are0
_ ...(23)2.4(2n + 2)(2n + 4) 1.J-n (t)(-1)n Jn (t)i is a positive integer
2.Jn+Z (t) =2tJ, (t) -(t)
3. dtto Jn-i (t).I = 0, we haveJo(t) = -J1(t).4.e 'h"-1/u) =1'Jn(t)unr(p) r(1- p)
-sin per '0 < p < 1 9!=-a This is called the generating function for the Bessel functions.8THE. LAPLACE TRANSFORM
5.J. (t) satisfies Bessel's differential . equation.
t2 Y11(t) + t Y'(t) + (t2 - n2) Y(t) _It is convenient to define
J0(it) = i-nIn(t) where I0(t)Bessel function of order n. III.The Error function is defined as
erf (t) =2e-u2 du 0 IV. The Complementary Error function is defined as erfc (t) =1erf (t).1 -2fte-u2du 0 V.The Sine and Cosine integrals are defined by
tSi (t)= fsin udu
0uCi (t)
VI.The Exponential integral is defined asf
Cos udutu
00 eudu5Ei (t)=(26) (27) (28) VII.The Unit Step function, also called Heaviside's unit function, is defined as 'U(t - a) _{0t < a(29)See Fig. 1-3.1t > a
u(t - a) i a t0 [CHAP. 1 is called the modified (24)5e_u2du
(25) I 1/EFig. 1-3
Fig. 1-4
VIII.The Unit Impulse function or Dirac delta function...Consider the function
FE (t)
quotesdbs_dbs13.pdfusesText_19[PDF] qqs
[PDF] niveau bright
[PDF] abréviation exemple
[PDF] test bright gratuit
[PDF] formule du demi-perimetre du rectangle
[PDF] mensuration homme musculation
[PDF] mesurer tour de cuisse homme
[PDF] orientation scolaire belgique
[PDF] conseiller d'orientation bruxelles
[PDF] vocabulaire géométrie collège
[PDF] test tricam
[PDF] exemple programme larp
[PDF] test paramétrique exercice corrigé
[PDF] test non paramétrique pdf
