 Inverse Laplace Transform
Inverse Laplace Transform
Inverse Laplace Transform. In this lecture we look at the problem of finding inverse Laplace transforms. In other words given how do we find.
 Inverse Laplace Transforms: Expressions with Error Functions
Inverse Laplace Transforms: Expressions with Error Functions
Auxiliary Sections > Integral Transforms > Tables of Inverse Laplace Transforms > Inverse Laplace Inverse transform f(x) = 1. 2πi. ∫ c+i∞ c−i∞ epx ˜f(p) ...
 What are and what are not
What are and what are not
https://ul.qucosa.de/api/qucosa%3A31590/attachment/ATT-0/
 Inverse Laplace Transforms: Expressions with Exponential Functions
Inverse Laplace Transforms: Expressions with Exponential Functions
Auxiliary Sections > Integral Transforms > Tables of Inverse Laplace Transforms > Inverse Laplace Inverse transform f(x) = 1. 2πi. ∫ c+i∞ c−i∞ epx ˜f(p) ...
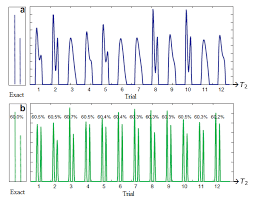 Regularization of the Inverse Laplace Transform with Applications in
Regularization of the Inverse Laplace Transform with Applications in
٠٦/١٢/٢٠١٦ Recover the distribution of amplitudes f(T2) present in the signal via an inverse Laplace transform (ILT). Christiana Sabett. ILT ...
 Inverse Laplace transforms via residue theory The Laplace
Inverse Laplace transforms via residue theory The Laplace
The in erse Laplace transform. The formula for the inverse Laplace transform was obtained in the previous section as: /(t) = 12πϳ/Х+ЦА. Е┴Х'ЦА. F(s)eЕtds. The
 The Inverse Laplace Transform and Analytic Pseudo-Differential
The Inverse Laplace Transform and Analytic Pseudo-Differential
Key Words: Laplace transform; inverse Laplace transform; pseudo-differential operators; differential operator of infinite order. 1. INTRODUCTION. w x. An
 The Inverse Laplace Transform
The Inverse Laplace Transform
We now know how to find Laplace transforms of “unknown” functions satisfying various initial- value problems. Of course it's not the transforms of those
 Inverse Laplace Transform - EqWorld
Inverse Laplace Transform - EqWorld
Inverse Laplace Transforms: Expressions with Inverse. Trigonometric Functions. No. Laplace transform. ˜f(p). Inverse transform
 Inverse Laplace Transform - EqWorld
Inverse Laplace Transform - EqWorld
Polyanin A. D. and Manzhirov
 6.3 Inverse Laplace Transforms
6.3 Inverse Laplace Transforms
Example 6.24 illustrates that inverse Laplace transforms are not unique. However it can be shown that
 The Inverse Laplace Transform
The Inverse Laplace Transform
26. The Inverse Laplace Transform. We now know how to find Laplace transforms of “unknown” functions satisfying various initial- value problems.
 Lecture XV: Inverse Laplace transform
Lecture XV: Inverse Laplace transform
07-Nov-2008 Inverse Laplace transform of a rational function poles zeros
 Chapter 7. Laplace Transforms. Section 7.4 Inverse Laplace
Chapter 7. Laplace Transforms. Section 7.4 Inverse Laplace
Chapter 7. Laplace Transforms. Section 7.4 Inverse Laplace Transform. Definition 1. Given a function F(s) if there is a function f(t) that is continuous on.
 Lecture : 2 (INVERSE LAPLACE TRANSFORMS)
Lecture : 2 (INVERSE LAPLACE TRANSFORMS)
L is called the inverse Laplace transformation operator. 2.2 Inverse Laplace Transform of some elementary functions: S. No. )( sF. 1.
 Section 7.4: Inverse Laplace Transform A natural question to ask
Section 7.4: Inverse Laplace Transform A natural question to ask
This idea has more than theoretical interest however; we'll see in the next section that finding inverse Laplace transforms is a critical step in solving
 Inverse Laplace Transform - EqWorld
Inverse Laplace Transform - EqWorld
Polyanin A. D. and Manzhirov
 Lecture 10 Solution via Laplace transform and matrix exponential
Lecture 10 Solution via Laplace transform and matrix exponential
Laplace transform of matrix valued function suppose z : R+ ? R convention: upper case denotes Laplace transform ... take inverse transform.
 Inverse Laplace Transform Practice Problems (Answers on the last
Inverse Laplace Transform Practice Problems (Answers on the last
(A) Continuous Examples (no step functions): Compute the inverse Laplace transform of the given function. • The same table can be used to find the inverse
 The Inverse Laplace Transform 1. If L{f(t)} = F(s) then the inverse
The Inverse Laplace Transform 1. If L{f(t)} = F(s) then the inverse
for any constant c. 2. Example: The inverse Laplace transform of. U(s) = 1 s3. +. 6.
 [PDF] The Inverse Laplace Transform
[PDF] The Inverse Laplace Transform
26 The Inverse Laplace Transform We now know how to find Laplace transforms of “unknown” functions satisfying various initial- value problems
 [PDF] Lecture : 2 (INVERSE LAPLACE TRANSFORMS) - Hansraj College
[PDF] Lecture : 2 (INVERSE LAPLACE TRANSFORMS) - Hansraj College
L is called the inverse Laplace transformation operator 2 2 Inverse Laplace Transform of some elementary functions: S No )( sF 1
 [PDF] Math 3331 Differential Equations - 53 The Inverse Laplace Transform
[PDF] Math 3331 Differential Equations - 53 The Inverse Laplace Transform
Basic Definition In-Class Exercises Partial Fractions Examples Examples 5 3 The Inverse Laplace Compute the inverse Laplace transform of Y (s) = 1
 [PDF] Chapter 8 LAPLACE TRANSFORMS AND INVERSE LAPLACE
[PDF] Chapter 8 LAPLACE TRANSFORMS AND INVERSE LAPLACE
An inverse Laplace transform of F(s) designated by L-¹{F(s)} is an- other function f(x) having the property that L{f(x)} = F(s) The simplest technique for
 [PDF] laplace transform
[PDF] laplace transform
Mostly used to find haplace Inverse Transformation for Example= t Find haplace of sex sin (1-x)dx
 [PDF] Table of Laplace Transformspdf - Purdue Math
[PDF] Table of Laplace Transformspdf - Purdue Math
6 8 Laplace Transform: General Formulas Formula Name Comments Sec F(s) = L{f(t))} = 00 e-stf(t) dt Definition of Transform 6 1 Inverse Transform
 [PDF] Inverse Laplace Transform :
[PDF] Inverse Laplace Transform :
The Inverse Laplace's transform for function denoted by defined as; iff ( ) (1) That form Laplace transform into the original function Example 1:
 [PDF] Chapter 7 Laplace Transforms Section 74 Inverse - TAMU Math
[PDF] Chapter 7 Laplace Transforms Section 74 Inverse - TAMU Math
Laplace Transforms Section 7 4 Inverse Laplace Transform Definition 1 Given a function F(s) if there is a function f(
 [PDF] The Inverse Laplace Transform 1 If L{f(t)} = F(s) then the inverse
[PDF] The Inverse Laplace Transform 1 If L{f(t)} = F(s) then the inverse
for any constant c 2 Example: The inverse Laplace transform of U(s) = 1 s3 + 6
 [PDF] TRANSFORMS
[PDF] TRANSFORMS
Methods of finding inverse Laplace transforms Partial fractions method Series methods Method of differential equations Differentiation
What is the inverse Laplace transform?
A Laplace transform which is a constant multiplied by a function has an inverse of the constant multiplied by the inverse of the function. First shift theorem: L ? 1 { F ( s ? a ) } = e a t f ( t ) , where f(t) is the inverse transform of F(s).What is the inverse Laplace transform of 1 /( s 4?
It is equivalent to 1(4?1)Does inverse Laplace transform exist?
Does such an inverse integral transform exist for the Laplace transform? Yes, it does In this section we will derive the inverse Laplace transform integral and show how it is used. and the inverse Fourier transform, g(t)=f(t)e?ct=12?????ˆg(?)e?i?td?.- A good first step is usually to reduce the function to partial fractions. Now the inverse Laplace transform of 2 (s?1) is 2e1 t.
Section 7.4: Inverse Laplace Transform
A natural question to ask about any function is whether it has an inverse function. We now ask this question about the Laplace transform: given a functionF(s), will there be a functionf(t) such thatF(s) =Lffg(s)? It turns out that there is at most one continuous functionf(t) which satises this property (there could be innitely many discontinuous functions with the same Laplace transform, but we prefer to work with continuous functions). Denition.Given a functionF(s), if there is a functionf(t) that is continuous on [0;1) and satisesLffg=F, then we say thatf(t) is the inverse Laplace transformofF(s) and employ the notationf=L1fFg. This idea has more than theoretical interest, however; we'll see in the next section that nding inverse Laplace transforms is a critical step in solving initial value problems. To determine the inverse Laplace transform of a function, we try to match it with the form of an entry in the right-hand column of a Laplace table.Example 1.DetermineL1fFgfor
(a)F(s) =2s3, (b)F(s) =3s
2+ 9, (c)F(s) =s1s
22s+ 5.
Solution.(a)L12s
3 (t) =L12!s 3 (t) =t2 (b)L13s 2+ 9 (t) =L13s 2+ 32 (t) = sin(3t) (c)L1s1s22s+ 5
(t) =L1s1(s1)2+ 22 (t) =etcos(2t). Of course, very often the transform we are given will not correspond exactly to an entry in the Laplace table. One tool we can use in handling more complicated functions is the linearity of the inverse Laplace transform, a property it inherits from the original Laplace transform. Theorem 1.Assume thatL1fFg;L1fF1g, andL1fF2gexist and are continuous on[0;1)and letcbe any constant. Then L1fF1+F2g=L1fF1g+L1fF2g;
L1fcFg=cL1fFg:
Example 2.DetermineL15s66ss
2+ 9+32s2+ 8s+ 10
Solution.By linearity, we have
L15s66ss
2+ 9+32s2+ 8s+ 10
= 5L11s6 6L1ss 2+ 9 +32L11s
2+ 4s+ 5
1 2 Rewriting the nal term using completing the square, it becomesL11(s+ 2)2+ 12Therefore, by the Laplace table we see that
L15s66ss
2+ 9+32s2+ 8s+ 10
(t) = 5e6t6cos(3t) +32 e2tsint:Example 3.DetermineL15(s+ 2)4
Solution.The fourth power in the denominator suggests that the inverse Laplace trans- form is of the form L1n!(sa)n+1
(t) =eattn:In this case,a=2;n= 3, so by linearity we have
L15(s+ 2)4
(t) =56L13!(s+ 2)4
(t) =56 e2tt3:Example 4.DetermineL13s+ 2s
2+ 2s+ 10
Solution.Using completing the square, the denominator can be rewritten as s2+ 2s+ 10 =s2+ 2s+ 1 + 9 = (s+ 1)2+ 32:
Therefore, the form ofF(s) suggests the following two formulas from the Laplace table: L1sa(sa)2+b2
(t) =eatcos(bt); L1b(sa)2+b2
(t) =eatsin(bt); where we havea=1;b= 3. Thus, we want to write3s+ 2s
2+ 2s+ 10=As+ 1(s+ 1)2+ 32+B3(s+ 1)2+ 32
for an appropriate choice of constantsA;B. By clearing the denominator, we have the equation3s+ 2 =A(s+ 1) + 3B=As+ (A+ 3B):
Equating coecients gives usA= 3;B=1=3, so by linearity, we have L13s+ 2s
2+ 2s+ 10
(t) = 3L1s+ 1(s+ 1)2+ 32 (t)13L13(s+ 1)2+ 32
(t) = 3etcos(3t)13 etsin(3t): 3 In Example 4, we found it easier to take the Laplace transform of the broken up fraction than of the original combined fraction. The procedure we used above, which you may recall from Calculus 2 and which will prove very useful in simplifying these functions, is called themethod of partial fractions. Because of its importance, we now review this method.Review of Partial FractionsA rational functionP(s)=Q(s), whereP(s);Q(s) are polynomials with the degree ofP
less than the degree ofQ, has a partial fraction expansion based on the factorization of Q. There are three main cases to consider, the easiest being that of nonrepeated linear factors. IfQ(s) is a product of distinct linear factors,Q(s) = (sr1)(sr2)(srn);
then the partial fraction expansion has the formP(s)Q(s)=A1sr1+A2sr2++Ansrn:
The constantsA1;:::;Ancan be derived by clearing denominators and either equating coecients of the resulting polynomials as in Example 4, or by careful substitution. We demonstrate the second way in the following examples. Example 5.DetermineL1fFgforF(s) =7s1(s+ 1)(s+ 2)(s3). Solution.Since the denominator has three distinct linear factors, the partial fraction expansion has the form7s1(s+ 1)(s+ 2)(s3)=As+ 1+Bs+ 2+Cs3;
and upon clearing denominators (multiplying through by (s+ 1)(s+ 2)(s3)), we have (1) 7s1 =A(s+ 2)(s3) +B(s+ 1)(s3) +C(s+ 1)(s+ 2): If we substitutes-values which make the linear factors zero, then each time two terms will drop out and it will be simple to solve for each coecient. First lets=1; then (1) becomes8 =4A)A= 2:
Similarly, lettings=2 gives
15 = 5B)B=3;
and lettings= 3 yields20 = 20C)C= 1:
4 Therefore, we can now use linearity to calculate the inverse Laplace transform: L17s1(s+ 1)(s+ 2)(s3)
(t) =L12s+ 13s+ 2+1s3 (t) = 2L11s+ 1 (t)3L11s+ 2 (t) +L11s3 (t) = 2et3e2t+e3t: The second scenario involves repeated linear factors. If the highest power ofsrthat dividesQ(s) is (sr)m, then the portion of the partial fraction expansion corresponding to (sr)mis A1sr+A2(sr)2++Am(sr)m:
Example 6.DetermineL1s2+ 9s+ 2(s1)2(s+ 3)
Solution.The partial fraction expansion has the form s2+ 9s+ 2(s1)2(s+ 3)=As1+B(s1)2+Cs+ 3:
Clearing denominators gives
(2)s2+ 9s+ 2 =A(s1)(s+ 3) +B(s+ 3) +C(s1)2: Again, we substitute values which make the linear factors vanish. Lettings= 1 in (2) gives12 = 4B)B= 3;
and lettings=3 yields16 = 16C)C=1:
To nd the third constant, we can plug in any other value fors; a convenient choice is s= 0:2 =3A+ 3B+C=3A+ 91
6 =3A)A= 2:
Therefore, the inverse Laplace transform is
L1s2+ 9s+ 2(s1)2(s+ 3)
(t) =L12s1+3(s1)21s+ 3 (t) = 2L11s1 (t) + 3L11(s1)2 (t)L11s+ 3 (t) = 2et+ 3tete3t: The most dicult case is that of a quadratic factor. Ifmis the highest power of (s)2+2that dividesQ(s), then the partial fraction expansion for that term is A1s+B1(s)2+2+A2s+B2[(s)2+2]2++Ams+Bm[(s)2+2]m:
5 However, for looking up Laplace transforms it is more convenient to have numerators of the formAi(s) +Bi, so we can equivalently write A1(s) +B1(s)2+2+A2(s) +B2[(s)2+2]++Am(s) +Bm[(s)2+2]m:
Example 7.DetermineL12s2+ 10s(s22s+ 5)(s+ 1)
Solution.Since the quadratic factor in the denominator is irreducible, we rewrite using completing the square:s22s+ 5 = (s1)2+ 22. Then the partial fraction expansion has the form2s2+ 10s(s22s+ 5)(s+ 1)=A(s1) + 2B(s1)2+ 22+Cs+ 1:Clearing denominators gives
(3) 2s2+ 10s= [A(s1) + 2B](s+ 1) +C(s22s+ 5): There are two linear terms involved in this expression, so pick the twos-values which make them vanish. Whens=1, we get8 = 8C)C=1:
Whens= 1, we get
12 = 4B+ 4C= 4B4)4B= 16)B= 4:
For the nal constant, sets= 0:
0 =A+ 2B+ 5C)A= 2(4) + 5(1) = 3:
Therefore, we nd the inverse Laplace transform to be L12s2+ 10s(s22s+ 5)(s+ 1)
=L13(s1) + 2(4)(s1)2+ 221s+ 1 = 3L1s1(s1)2+ 22 + 4L12(s1)2+ 22L11s+ 1
= 3etcos(2t) + 4etsin(2t)et:Homework: pp. 374-375, #1-29 odd.
quotesdbs_dbs13.pdfusesText_19[PDF] qqs
[PDF] niveau bright
[PDF] abréviation exemple
[PDF] test bright gratuit
[PDF] formule du demi-perimetre du rectangle
[PDF] mensuration homme musculation
[PDF] mesurer tour de cuisse homme
[PDF] orientation scolaire belgique
[PDF] conseiller d'orientation bruxelles
[PDF] vocabulaire géométrie collège
[PDF] test tricam
[PDF] exemple programme larp
[PDF] test paramétrique exercice corrigé
[PDF] test non paramétrique pdf
