FICHE - LE CÔNE DE RÉVOLUTION - lewebpedagogiquecom

[PDF] calculer le patron d'un cone

[PDF] barycentre triangle équilatéral

[PDF] barycentre triangle rectangle

[PDF] barycentre exercices corrigés

[PDF] calcul angle triangle en ligne

[PDF] comment calculer la hauteur d une construction

[PDF] calcul hauteur batiment plu

[PDF] comment calculer la hauteur d'un pignon de maison

[PDF] comment calculer la hauteur d'un arbre

[PDF] calculer la hauteur d'une pyramide sans le volume

[PDF] hauteur pyramide egypte

[PDF] calculer la hauteur de la pyramide du louvre

[PDF] comment calculer la hauteur d'une pyramide 4eme

[PDF] calculer la hauteur d'une pyramide avec thales

[PDF] comment calculer le perimetre d un rectangle sur s

FICHE - LE CÔNE DE RÉVOLUTION

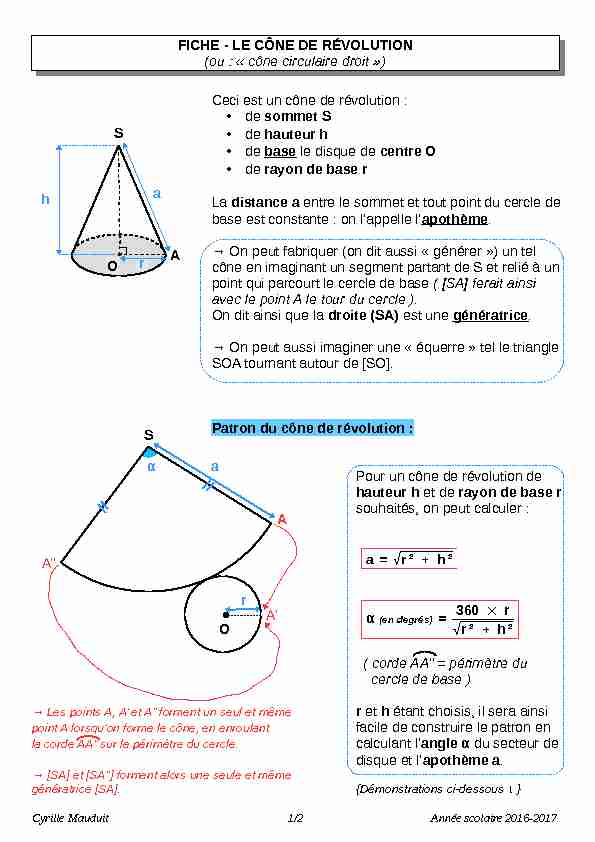
(ou : " cône circulaire droit »)

Ceci est un cône de révolution :

•de sommet S •de hauteur h •de base le disque de centre O •de rayon de base r La distance a entre le sommet et tout point du cercle de base est constante : on l'appelle l'apothème. → On peut fabriquer (on dit aussi " générer ») un tel cône en imaginant un segment partant de S et relié à un point qui parcourt le cercle de base ( [SA] ferait ainsi avec le point A le tour du cercle ). On dit ainsi que la droite (SA) est une génératrice. → On peut aussi imaginer une " équerre » tel le triangle

SOA tournant autour de [SO].

Patron du cône de révolution :

Pour un cône de révolution de

hauteur h et de rayon de base r souhaités, on peut calculer :a = √r² + h²

α (en degrés) = 360 × r

√r² + h² ( corde AA'' = périmètre du cercle de base ) → Les points A, A' et A'' forment un seul et mêmer et h étant choisis, il sera ainsi point A lorsqu'on forme le cône, en enroulantfacile de construire le patron en la corde AA'' sur le périmètre du cercle.calculant l'angle α du secteur de disque et l'apothème a. → [SA] et [SA''] forment alors une seule et même génératrice [SA].{Démonstrations ci-dessous ↓ }

Cyrille Mauduit1/2Année scolaire 2016-2017S

A Oah r rS A''A

OA'aα

×kDémonstrations :

•Dans le triangle SOA rectangle en O, si l'on applique le théorème de Pythagore, on trouve alors que :

SA² = SO² + OA²

a² = h² + r² D'où l'égalité suivante :a = √r² + h² •→ Un angle α peut être exprimé avec deux unités de mesure possibles, proportionnelles l'une à l'autre : les degrés (°) et les radians (rad). α (°)0°30°45°60°90°180°360°

α (rad)0

6 4 3 2

π2π

Avec :k = 2π

360
On trouve ainsi qu'en général :α(°) = α(rad)×360

2π(produit en croix)

→ Il faut savoir aussi que par définition : L'angleα(rad)d'unsecteurdedisque = cordedusecteurdedisque rayondudisque, soit ici pour le secteur de disque de rayon l'apothème SA = a :

α(rad) = AA''

adonc d'après la formule précédente :α(rad) = AA''√r² + h² Or ici, nous savons que la corde AA'' est de même longueur que le périmètre du disque de base de rayon r, donc :

AA'' =

2πrd'où :α(rad) = 2πr

√r² + h²→ En utilisant la relation de conversion entre les radians et les degrés (produit

en croix ci-dessus), on trouve finalement que :

α(°) = α(rad)×360

2π = 2πr

√r² + h²×360

2πd'où :

α (en degrés) = 360 × r

√r² + h²

Cyrille Mauduit2/2Année scolaire 2016-2017

quotesdbs_dbs2.pdfusesText_3

[PDF] FICHE - LE CÔNE DE RÉVOLUTION - lewebpedagogiquecom

Chapitre 20 Cône de révolution - ac-versaillesfr

Chapitre 20 Cône de révolution - Créer son blog