Classe de Troisième
1) Propriété 1 : Si a et b sont deux nombres positifs alors : axb = a x b. Exemple : 48 = 16 x 3. = 16 x 3. = 4 x 3. = 4 3. 2) Propriété
chapitre (Racines carr�es)
FONCTIONS AFFINES (Partie 2)
Soit une fonction affine f : x ax + b représentée dans un repère par une droite d. Les coordonnées (x ; y) d'un point M appartenant à d vérifient y = ax + b
Fonct aff
Identités remarquables
On reconnaît une expression du type a² + 2ab + b² avec a = x et b = 3. Vérifions : a² = x² ; b² = 9 ; 2ab = 2хxх3 = 6x . KB 1 sur 2
identites
SECOND DEGRE (Partie 2)
En effet a = 3
Secondegre ESL
Tableaux des dérivées
%20primitives
) Quelques formules de trigonométrie vraiment utiles. a
Equation d'une droite
1- Si la droite D d'équation y = ax+b passe par les points A(xA; yA) et B(xB; yB) alors le coefficient directeur a est égal à. yB−yA. xB−xA . 2- La droite D
droites
LES FONCTIONS DE REFERENCE
f x ax b. = + . Si. 0 a > alors f est croissante sur ℝ. Déterminer par calcul une expression de la fonction f telle que f (-2) = 4 et f (3) = 1.
Fonctions reference
les matrices sur Exo7
Comme la multiplication n'est pas commutative les identités binomiales usuelles sont fausses. En particulier
ch matrices
SECOND DEGRÉ (Partie 1)
Cette dernière écriture s'appelle la forme canonique de f. Démonstration : Comme a ≠ 0 on peut écrire pour tout réel x : f (x) = ax2 + bx + c. = a x2 + b.
Secondegre
Tableaux des primitives usuelles Toutes les primitives de ces
29 avr. 2010 f (x) = ax + b. F (x) = 1. 2 ax² + bx + k. ℝ f (x) = xn n entier différent de –1 ... 0[ ou ]0; +∞[ si n –2.
tableaux primitives
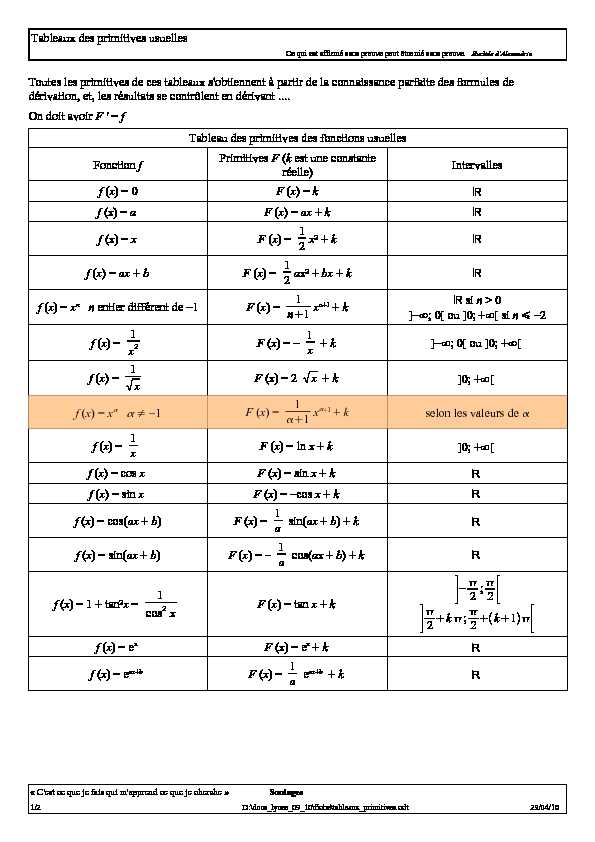
Tableaux des primitives usuelles
Ce qui est affirmé sans preuve peut être nié sans preuve. Euclide d'AlexandrieToutes les primitives de ces tableaux s'obtiennent à partir de la connaissance parfaite des formules de
dérivation, et, les résultats se contrôlent en dérivant ....On doit avoir F ' = f
Tableau des primitives des fonctions usuelles
Fonction fPrimitives F (k est une constante
réelle)Intervalles f (x) = 0F (x) = kℝ f (x) = a F (x) = ax + kℝ f (x) = xF (x) = 12x² + kℝ
f (x) = ax + bF (x) = 12ax² + bx + kℝ
f (x) = xn n entier différent de -1F (x) = 1 n1xn+1 + kℝ si n > 0 ]-∞; 0[ ou ]0; +∞[ si n -2 f (x) = 1 x2 F (x) = - 1 x + k ]-∞; 0[ ou ]0; +∞[ f (x) = 1 x F (x) = 2 x + k ]0; +∞[ f (x) = x ≠ -1F (x) = 1 1x+1 + kselon les valeurs de f (x) = 1 x F (x) = ln x + k ]0; +∞[ f (x) = cos x F (x) = sin x + k ℝ f (x) = sin x F (x) = -cos x + k ℝ f (x) = cos(ax + b)F (x) = 1 a sin(ax + b) + k ℝ f (x) = sin(ax + b)F (x) = - 1 a cos(ax + b) + k ℝ f (x) = 1 + tan²x = 1 cos2 x F (x) = tan x + k2;
2[2k;
2k1[f (x) = ex F (x) = ex + k ℝ
f (x) = eax+b F (x) = 1 a eax+b + k ℝ " C'est ce que je fais qui m'apprend ce que je cherche » Soulages1/2 D:\docs_lycee_09_10\fiche\tableaux_primitives.odt 29/04/10
Tableaux des primitives usuelles
Ce qui est affirmé sans preuve peut être nié sans preuve. Euclide d'AlexandriePrimitives et opérations
u et v sont des fonctions de primitives respectives U et V Fonction f Une primitive F (déterminée à une constante près)Remarques f = u + v F = U + V f = ku (k constante)F = kU Dans la suite u est dérivable sur un intervalle I f = u' un (n ≠ -1)F = 1 n1un+1 selon les valeurs de n f = u' u2 F = - 1 uu ne s'annule pas sur I f = u '×cosuF = sin u f = u '×sinuF = - cos u f = u' u F = ln u si u > 0 F = ln (-u) si u < 0étudier le signe de u (x) ... f = u' u F = 2 u u > 0 f = u '×euF = eu f = u' ×(v' °u)F = v ° u conditions d'existence et de dérivabilité de v ° u. f F (x) = ∫ax ftdt f continue sur I a ∈ IF est la primitive définie sur I de f
qui s'annule en aIntégration par parties:
u, v dérivables et leurs dérivées u' et v' sont continues sur I. f = uv'F (x) = ∫ax
utv'tdt = [utvt]ax - ∫a x u'tvtdt " C'est ce que je fais qui m'apprend ce que je cherche » Soulages2/2 D:\docs_lycee_09_10\fiche\tableaux_primitives.odt 29/04/10
Tableaux des primitives usuelles
Ce qui est affirmé sans preuve peut être nié sans preuve. Euclide d'AlexandrieToutes les primitives de ces tableaux s'obtiennent à partir de la connaissance parfaite des formules de
dérivation, et, les résultats se contrôlent en dérivant ....