 Exercices corrigés - limites
Exercices corrigés - limites
LIMITES – EXERCICES CORRIGES. Exercice n°1. Déterminer la limite éventuelle en Retrouver les limites de f(x) à partir du graphique connaissant les asymptotes.
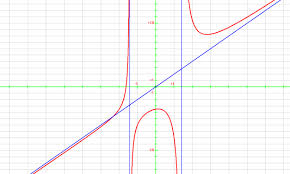 1 Limites et comportement asymptotique Exercices corrigés
1 Limites et comportement asymptotique Exercices corrigés
(asymptote verticale et asymptote horizontale). • Exercice 2 : étude de limites asymptotes verticales et horizontales. • Exercice 3 : étude de limites de
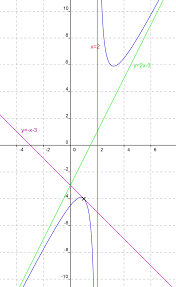 Limites de fonctions et asymptotes - Exercices Fiche 2
Limites de fonctions et asymptotes - Exercices Fiche 2
Déterminer la limite de f en + et en - . 4. Montrer que la courbe C f représentative de la fonction f admet une asymptote en + et en - .
 Limites et asymptotes corrigés
Limites et asymptotes corrigés
= +∞. = −∞ : la droite d'équation. 3 x = est asymptote verticale à la courbe représentative de f. Exercice 8 : La courbe ci-dessous représente une fonction f
 Limites et comportement asymptotique Exercices corrigés - AlloSchool
Limites et comportement asymptotique Exercices corrigés - AlloSchool
(asymptote verticale et asymptote horizontale). • Exercice 2 : étude de limites asymptotes verticales et horizontales. • Exercice 3 : étude de limites de
 Dérivées II: variations et asymptotes exercices maths standard
Dérivées II: variations et asymptotes exercices maths standard
corriges/index.html. 3s - Dérivées II : variations et asymptotes. Matières. Dérivées et monotonie ; tableau de variations ; limites et asymptotes. Exercice 1.
 Limites – Corrections des Exercices
Limites – Corrections des Exercices
Correction : On déduit de la question précédente que la droite d'équation x = 1/3 est une asymptote verticale. —. -9-. Page 10. DAEU-B – Maths.
 Chapitre 2: Limites et Asymptotes
Chapitre 2: Limites et Asymptotes
Exercice 2.6: Déterminer ED(f) et calculer les limites à gauche et à droite des valeurs interdites. 1) f (x) = 12 −2x. 3− x. 2) f (x)
 Asymptotes exercices corrigés pdf
Asymptotes exercices corrigés pdf
Limites asymptotes exercices corrigés. Limites et asymptotes exercices corrigés. Exercices corrigés sur les asymptotes. Exercices asymptotes corrigés terminale
 Limites asymptotes EXOS CORRIGES
Limites asymptotes EXOS CORRIGES
M. CUAZ http://mathscyr.free.fr. Page 1/18. LIMITES – EXERCICES CORRIGES. Exercice n°1. Déterminer la limite éventuelle en + ? de chacune des fonctions
 1 Limites et comportement asymptotique Exercices corrigés
1 Limites et comportement asymptotique Exercices corrigés
Sont abordés dans cette fiche : • Exercice 1 : détermination graphique d'une limite et d'une équation d'asymptote à une courbe. (asymptote verticale et
 Limites de fonctions et asymptotes - Exercices Fiche 2
Limites de fonctions et asymptotes - Exercices Fiche 2
Déterminer la limite de f en + et en - . 4. Montrer que la courbe C f représentative de la fonction f admet une asymptote en + et en - .
 I Exercices
I Exercices
Calculer les limites des fonctions suivantes et préciser lorsque la courbe représentative de f (notée (Cf )) admet une asymptote horizontale. 1. f(x) = x3 ?
 Limites-et-asymptotes-corriges.pdf
Limites-et-asymptotes-corriges.pdf
= ? : la droite d'équation. 5 y = ? est asymptote horizontale à la courbe représentative de f. Exercice 7 : a). 0 lim ( ) x.
 Dérivées II: variations et asymptotes exercices maths standard
Dérivées II: variations et asymptotes exercices maths standard
Lien vers la page mère : Exercices avec corrigés sur www.deleze.name Dérivées et monotonie ; tableau de variations ; limites et asymptotes. Exercice 1.
 Limites et comportement asymptotique Exercices corrigés - AlloSchool
Limites et comportement asymptotique Exercices corrigés - AlloSchool
Sont abordés dans cette fiche : • Exercice 1 : détermination graphique d'une limite et d'une équation d'asymptote à une courbe.
 Limites et asymptotes et etudes de fonctions
Limites et asymptotes et etudes de fonctions
Construire avec un tableau de variation. Pour les exercices de 1 à 4 utiliser le tableau de variations pour trouver le domaine de définition
 Chapitre 2: Limites et Asymptotes
Chapitre 2: Limites et Asymptotes
voisinage d'un trou ou d'un bord (point limite ou asymptote verticale) de son Exercice 2.3: Esquisser le graphe de la fonction f définie par f (x) = 2? ...
 Limites – Corrections des Exercices
Limites – Corrections des Exercices
Correction : On déduit de la question précédente que la droite d'équation x = 1/3 est une asymptote verticale. —. -9-. Page 10. DAEU-B – Maths.
I Exercices
1 Limites sans ind´etermination
Calculer les limites des fonctions suivantes, et pr´eciserlorsque la courbe repr´esentative def(not´ee (Cf)) admet une asymptote horizontale ou verticale.1.f(x) =x2+ 2x-3 en +∞.
2.f(x) =x3-6x2+ 1 en-∞.
3.f(x) =1
(x+ 1)2en +∞.4.f(x) =-⎷
x+1xen +∞.5.f(x) = (-x+ 3)5en +∞.
6.f(x) = (-x+ 3)5en-∞.
7.f(x) = (4-2x)2en +∞.
8.f(x) =-5⎷
x2-1 en-∞.9.f(x) =x2-3x+ 1 en 2.
10.f(x) =-3
⎷2-xen 2 par valeurs inf´erieures.11.f(x) =2x-3
x-1en 1 par valeurs inf´erieures.12.f(x) =2x-3
x-1en 1 par valeurs sup´erieures.13.f(x) =5
4-x2en-2 par valeurs inf´erieures.
14.f(x) =5
4-x2en-2 par valeurs sup´erieures.
R´eponses
2 Limite en l"infini d"un polynˆome ou d"une fraction rationnelle
Calculer les limites des fonctions suivantes, et pr´eciserlorsque la courbe repr´esentative def(not´ee (Cf)) admet une asymptote horizontale.1.f(x) =x3-2x+ 3, en +∞.
2.f(x) =x+ 3
2x-1en-∞.
3.f(x) =x4+xen-∞.
4.f(x) =x2-2
2x+ 3en-∞.
5.f(x) =2x-5
x+x2en +∞.6.f(x) =4-2x4
x2(x+ 1)2en-∞.Aide7.f(x) =(3x+ 1)2(2x-3)3en +∞.R´eponses
L.BILLOT 1DDL
de la 1`ereS `a la TS. Chapitre 2 : Limites et asymptotes3 Limites ind´etermin´ees
Pour chaque limite il faut trouver la bonne m´ethode. C"est difficile au d´ebut, puis avec l"exp´erience ....Calculer les limites suivantes
1. lim
x→+∞x+ sinx.2. lim
x→+∞sinx x.3. lim
x→+∞⎷ x-3-⎷x+ 1.4. lim
x→0cosx-1 x.5. lim
x→0⎷ x+ 1-1 x.6. lim
x→+∞⎷ x2-1-2x.7. lim x→-∞⎷2x2-5 + 2x.
8. lim
x→32x2-5x-3 x2-9.9. lim
x→0sinx x.10. lim
x→+∞3x-54 + sinx.
11. lim
x→-∞x2-5cosx. AideR´eponses
4 Asymptotes obliques
1. On consid`ere la fonction d´efinie surR-{-2;2}par :f(x) =2x3-x2-8x+ 7
x2-4, et on appelle (Cf) sa courbe repr´esentative dans un rep`ere du plan. (a) Montrer que la droite (Δ) d"´equationy= 2x-1 est asymptote `a la courbe en (b) ´Etudier les positions relatives de (Cf) et de (Δ).2. On consid`ere la fonctionfd´efinie surR- {-2}parf(x) =x2-x-3
x+ 2. On note (Cf) sa courbe. (a) D´eterminer des r´eelsa, betctels que :f(x) =ax+b+c x+ 2. (b) En d´eduire que (Cf) admet une asymptote en-∞et donner l"´equation de cette asymptote.3. On donne la fonctionfd´efinie sur ]- ∞;0]?[4;+∞[ par :f(x) =⎷
x2-4x. Montrer que la droite d"´equationy=x-2 est asymptote `a la courbe repr´esentative defen +∞4. (a) Montrer que la courbe repr´esentative de la fonctiong, d´efinie parg(x) =x3+ 4
x2 admet une asymptote oblique en +∞. (b) D´eterminer sur quel ensemble l"´ecart entre la courbe et l"asymptote est inf´erieur `a un centi`eme d"unit´e. AideR´eponses
L.BILLOT 2DDL
de la 1`ereS `a la TS. Chapitre 2 : Limites et asymptotesII Aide
2 Limite en l"infini d"un polynˆome ou d"une fraction rationnelle
Premi`ere m´ethode :
Je mets le terme de plus haut degr´e en facteur, je simplifie dans le cas d"une fraction, puis je calcule la limite.Deuxi`eme m´ethode :
J"applique une des r`egles suivantes :
La limite en l"infini d"un polynˆome est ´egale `a la limite deson terme de plus haut degr´e. La limite en l"infini d"une fraction rationnelle est ´egale `a la limite du quotient de ses termes de plus haut degr´e.Retour
3 Limites ind´etermin´ees
Quelques m´ethodes pour lever une ind´etermination : Les r`egles de comparaison de fonctions : in´egalit´es, th´eor`eme des gendarmes. Utilisation possible : limites en l"infini d"une fonction trigo.L"expression conjugu´ee.Utilisation possible : limites avec des sommes ou des diff´erences contenant des ra-
cines.Retour `a la d´efinition du nombre d´eriv´e.Utilisation possible : limites d"un quotient en un point. (avec ´eventuellement des
diff´erences au num´erateur et au d´enominateur)Factorisation.Utilisation possible : limites en l"infini avec des racines,ou limites en un point de
fractions.Aide sp´ecifique `a chaque question :
1. Comparaison.
2. Comparaison (gendarmes).
3. Expression conjugu´ee.
4. Nombre d´eriv´e.
5. Nombre d´eriv´e ou expression conjugu´ee.
6. Factorisation.
7. Factorisation. Attention, six <0,⎷
x2?=x.8. Factorisation.
9. Nombre d´eriv´e.
10. Comparaison.
11. Comparaison.
Retour
L.BILLOT 3DDL
de la 1`ereS `a la TS. Chapitre 2 : Limites et asymptotes4 Asymptotes obliques
Rappel de cours :
Soitfune fonction et (Cf) sa courbe repr´esentative, alors les deux propri´et´es suivantes sont ´equivalentes : La droite (d) d"´equationy=ax+best asymptote `a (Cf) en +∞ssi lim x→+∞(f(x)-(ax+b)) = 0 La droite (d) d"´equationy=ax+best asymptote `a (Cf) en +∞ssi il existe une fonction?telle que : f(x) =ax+b+?(x) avec limx→+∞?(x) = 0 (La fonction?repr´esente l"´ecart entre la courbe et la droite.)Mˆeme chose si je remplace +∞par-∞.
M´ethodes :
Si dans le texte on me donne l"´equation de l"asymptote, alors je simplifie l"expression def(x)-(ax+b), puis je calcule la limite. Si on ne me donne pas l"´equation , j"essaie de reconnaˆıtre la formeax+b+?(x). Pour d´eterminer les positions relatives, j"´etudie le signe de la diff´erence : f(x)-(ax+b).Retour
L.BILLOT 4DDL
de la 1`ereS `a la TS. Chapitre 2 : Limites et asymptotesIII Correction
1 Limites sans ind´etermination
1. lim x→+∞x2= +∞ lim x→+∞2x= +∞ lim x→+∞-3 =-3??????? donc limx→+∞x2+ 2x-3 = +∞. 2. lim x→-∞x3=-∞ lim x→-∞x2= +∞donc limx→-∞-6x2=-∞ lim x→-∞1 = 1??????? donc limx→-∞x3-6x2+ 1 =-∞. 3. limx→+∞1 = 1 lim x→+∞(x+ 1)2= +∞? donc lim x→+∞1 (x+ 1)2= 0. La courbe (Cf) admet une asymptote horizontale d"´equationy= 0 en +∞. 4. limx→+∞-⎷ x=-∞ lim x→+∞1 x= 0??? donc limx→+∞-⎷ x+1x=-∞.5. lim
x→+∞(-x+ 5) =-∞, donc limx→+∞(-x+ 3)5=-∞.6. lim
x→-∞(-x+ 3) = +∞, donc limx→-∞(-x+ 3)5= +∞.7. lim
x→+∞(4-2x) =-∞, donc limx→+∞(4-2x)2= +∞. 8. limx→-∞-5 =-5 lim x→-∞(x2-1) = +∞donc limx→+∞⎷ x2-1 = +∞??? donc limx→-∞-5⎷x2-1= 0. La courbe (Cf) admet une asymptote horizontale d"´equationy= 0 en-∞. 9. lim x→2x2= 4 lim x→2-3x=-6 lim x→2+ = 1??????? donc limx→2x2-3x+ 1 =-1. 10. lim x <→2-3 =-3 lim x <→22-x= 0+donc lim x <→2⎷2-x= 0+???
donc lim x <→2-3⎷2-x=-∞. La courbe (Cf) admet une asymptote verticale d"´equationx= 2.Retour
L.BILLOT 5DDL
de la 1`ereS `a la TS. Chapitre 2 : Limites et asymptotes11.lim
x <→12x-3 =-1 lim x <→1x-1 = 0-??? donc lim x <→12x-3x-1= +∞. La courbe (Cf) admet une asymptote verticale d"´equationx= 1. 12. lim x >→12x-3 =-1 lim x >→1x-1 = 0+??? donc lim x >→12x-3 x-1=-∞. La courbe (Cf) admet une asymptote verticale d"´equationx= 1. 13. lim x <→-25 = 5 lim x <→-24-x2= 0-??? donc lim x <→-254-x2=-∞.
La courbe (Cf) admet une asymptote verticale d"´equationx=-2. 14. lim x >→-25 = 5 lim x >→-24-x2= 0+??? donc lim x >→-254-x2= +∞.
La courbe (Cf) admet une asymptote verticale d"´equationx=-2.Retour
2 Limite en l"infini d"un polynˆome ou d"une fraction rationnelle
1. Premi`ere m´ethode :
f(x) =x3?1-2x2+3x3?
Or lim
x→+∞x3= +∞et limx→+∞? 1-2 x2+3x3? = 1, donc lim x→+∞f(x) = +∞.Deuxi`eme m´ethode :
limx→+∞x3-2x+ 3 = limx→+∞x3= +∞.2. Premi`ere m´ethode :
f(x) =x?1 +3x? x?2-1x? =1 +3 x 2-1x.Or lim
x→-∞? 1 +3 x? = 1 et lim x→-∞? 2-1x? = 2, donc lim x→-∞f(x) =12.Deuxi`eme m´ethode :
limx→-∞x+ 32x-1= limx→-∞x2x= limx→-∞12=12. Donc la courbe (Cf) admet une asymptote horizontale d"´equationy=12en-∞.
Remarque :La deuxi`eme m´ethode ´etant plus rapide, j"utiliserais dor´enavant celle- ci dans les calculs. Mais attention : Cette m´ethode ne s"applique qu"en + ou - l"infini. Cette m´ethode ne s"applique p=pas lorsque l"on a des fonctions racines, trigono- m´etriques, logarithmes ....L.BILLOT 6DDL
de la 1`ereS `a la TS. Chapitre 2 : Limites et asymptotesRetour
3. limx→-∞x4+x= limx→-∞x4= +∞.
4. lim
x→-∞x 2-22x+ 3= limx→-∞x
22x= limx→-∞x2=-∞.
5. lim
x→+∞2x-5 x+x2= limx→+∞2xx2= limx→+∞2x= 0. (Cf) admet une asymptote horizontale d"´equationy= 0 en +∞.6. lim
x→-∞4-2x4 x2(x+ 1)2= limx→-∞-2x4x4= limx→-∞-2 =-2. (Cf) admet une asymptote horizontale d"´equationy=-2 en-∞.7. lim
x→+∞(3x+ 1)2 (2x-3)3= limx→+∞9x28x3= limx→+∞98x= 0. (Cf) admet une asymptote horizontale d"´equationy= 0 en +∞.Retour
3 Limites ind´etermin´ees
1. Pour toutx?R,sinx?-1, doncx+ sinx?x-1.
Or lim
x→+∞x-1 = +∞, donc limx→+∞x+ sinx= +∞.2. Pour toutx?R,-1?sinx?1, donc six >0, on a :-1
x?sinxx?1x.Or lim
x→+∞-1 x= 0 et limx→+∞1x= 0, donc limx→+∞sinxx= 0.3. Pour toutx >1,⎷
x-3-⎷x+ 1 =(⎷x-3-⎷x+ 1)(⎷x-3 +⎷x+ 1)⎷x-3 +⎷x+ 1= (x-3)-(x+ 1) ⎷x-3 +⎷x+ 1=-4⎷x-3 +⎷x+ 1.Or lim
x→+∞⎷x-3 = +∞et limx→+∞⎷x+ 1 = +∞, donc limx→+∞⎷x-3+⎷x+ 1 = +∞
et lim x→+∞-4 ⎷x-3 +⎷x+ 1= 04. Rappel : sifest d´erivable enaalors limx→af(x)-f(a)
x-a=f?(a). La fonctionx?→cosxest d´erivable en 0 et sa d´eriv´ee est :x?→ -sinx, donc :lim x→0cosx-1 x= limx→0cosx-cos0x-1=-sin0 = 0.5. La fonctionx?→⎷
x+ 1 est d´erivable en 0 et sa d´eriv´ee est :x?→12⎷x+ 1, lim x→0⎷ x+ 1-1 x= limx→0⎷ x+ 1-⎷0 + 1 x-0=12⎷0 + 1=12.6. Pourx >0,⎷
x2-1-2x=?x2?1-1x2?
-2x=⎷x2?1-1x2-2x=x? ?1-1x2-2?Or lim
x→+∞x= +∞et limx→+∞?1-1x2-2?
=-1, donc limx→+∞⎷x2-1-2x=-∞.L.BILLOT 7DDL
de la 1`ereS `a la TS. Chapitre 2 : Limites et asymptotes7. Icixest n´egatif, donc⎷x2=-x.
Pourx <0,⎷
2x2-5+2x=?x2?
2-5x2?
+2x=-x?2-5x2+2x=x? -?2-5x2+ 2?Or lim
x→-∞x=-∞et limx→-∞?2-5x2+ 2?
=-⎷2 + 2>0, donc limx→-∞f(x) =8. 3 annule le num´erateur et le d´enominateur, donc il sont tous les deux factorisables
parx-3.Pour toutx?= 3,2x2-5x-3
x2-9=(x-3)(2x+ 1)(x-3)(x+ 3)=2x+ 1x+ 3.Donc lim
x→32x2-5x-3 x2-9= limx→32x+ 1x+ 3=76.9. La fonction sinus est d´erivable surRet sa d´eriv´ee est la fonction cosinus , donc
lim x→0sinx x= limx→0sinx-sin0x-0= cos0 = 1.10. Pour toutx?R,sinx?1, donc 4+sinx?5 donc1
4 + sinx?3x-55et3x-54 + sinx?
1 5Or lim
x→+∞3x-55= +∞, donc limx→+∞3x-54 + sinx= +∞.
11. Pour toutx?R,cosx?1, doncx2-5cosx?x2-5, or limx→-∞x2-5 = +∞, donc
lim x→-∞x2-5cosx= +∞.Retour
4 Asymptotes obliques
1. (a) Pour toutx?R- {-2,2},
f(x)-(2x-1) =2x3-x2-8x+ 7-(2x-1)(x2-4) x2-4=3x2-4. limx→+∞(x2-4) = +∞, donc limx→+∞(f(x)-(2x-1)) = 0 et la droite (Δ) d"´equation
y= 2x-1 est asymptote `a la courbe en +∞. (b) J"´etudie le signe def(x)-(2x-1)) =3 x2-4. x2-4 est un trinˆome du second degr´e dont les racines sont-2 et 2.
Donc :
3 x2-4est positif et la courbe est au dessus de son asymptote sur ]- ∞;-2[?]2;+∞[ 3 x2-4est n´egatif et la courbe est en dessous de son asymptote sur ]-2;2[. (Les intervalles sont ouverts, car ce sont des valeurs qui annulent le d´enomina- teur.)L.BILLOT 8DDL
de la 1`ereS `a la TS. Chapitre 2 : Limites et asymptotes2. (a) Pour toutx?=-2,ax+b+cx+ 2=(ax+b)(x+ 2) +cx+ 2=ax2+ (2a+b)x+ 2b+cx+ 2.
J"identifie les coefficients du num´erateur avec ceux de x2-x-3 x+ 2, ce qui donne : ?a= 12a+b=-1
2b+c=-3????a= 1
b=-3 c= 3, doncf(x) =x-3 +3 x+ 2. (b)f(x) =x-3+3 x+ 2, avec limx→-∞3x+ 2= 0 donc (Cf) admet la droite d"´equation y=x-3 comme asymptote en-∞.3.f(x)-(x-2) =⎷
x2-4x-(x-2) =(⎷x2-4x-(x-2))(⎷x2-4x+ (x-2))⎷x2-4x+ (x-2)= -4 ⎷x2-4x+ (x-2)Or lim
x→+∞⎷ x2-4x= limx→+∞x?1-4x= +∞et limx→+∞(x-2) = +∞, donc lim x→+∞-4 ⎷x2-4x+ (x-2)= 0. Donc la droite d"´equationy=x-2 est bien asymptote `a la courbe repr´esentative defen +∞4. (a) Pour toutx?R?,g(x) =x3+ 4
x2=x+4x2, et limx→+∞4x2= 0, donc la droite d"´equationy=xest asymptote oblique en +∞`a la courbe. (b) L"´ecart entre deux courbes est donn´ee par la valeur absolue de la diff´erence, donc je r´esous |f(x)-x|?10-2 ?????4 x2???? ?10-2 4 x2?10-2 ?x2?400 ?x?]- ∞;-20]?[20;+∞[.Retour
L.BILLOT 9DDL
quotesdbs_dbs47.pdfusesText_47[PDF] limites et continuité cours bac pdf
[PDF] limites et continuité exercices corrigés
[PDF] limites et continuité exercices corrigés bac
[PDF] limites et continuité exercices corrigés bac maths
[PDF] limites et continuité exercices corrigés bac pdf
[PDF] limites et continuité exercices corrigés bac science
[PDF] limites et continuité exercices corrigés mpsi
[PDF] limites et continuité exercices corrigés pdf
[PDF] Limites et convexité
[PDF] Limites et étude de fonctions
[PDF] Limites et fonctions
[PDF] limites et fonctions composée
[PDF] Limites et formes indeterminées
[PDF] Limites et propriétés
