 Exercices corrigés - limites
Exercices corrigés - limites
LIMITES – EXERCICES CORRIGES. Exercice n°1. Déterminer la limite éventuelle en Retrouver les limites de f(x) à partir du graphique connaissant les asymptotes.
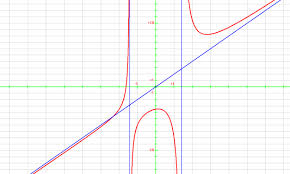 1 Limites et comportement asymptotique Exercices corrigés
1 Limites et comportement asymptotique Exercices corrigés
(asymptote verticale et asymptote horizontale). • Exercice 2 : étude de limites asymptotes verticales et horizontales. • Exercice 3 : étude de limites de
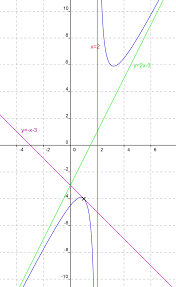 Limites de fonctions et asymptotes - Exercices Fiche 2
Limites de fonctions et asymptotes - Exercices Fiche 2
Déterminer la limite de f en + et en - . 4. Montrer que la courbe C f représentative de la fonction f admet une asymptote en + et en - .
 Limites et asymptotes corrigés
Limites et asymptotes corrigés
= +∞. = −∞ : la droite d'équation. 3 x = est asymptote verticale à la courbe représentative de f. Exercice 8 : La courbe ci-dessous représente une fonction f
 I Exercices
I Exercices
Calculer les limites des fonctions suivantes et préciser lorsque la courbe représentative de f (notée (Cf )) admet une asymptote horizontale. 1. f(x) = x3 −
 Limites et comportement asymptotique Exercices corrigés - AlloSchool
Limites et comportement asymptotique Exercices corrigés - AlloSchool
(asymptote verticale et asymptote horizontale). • Exercice 2 : étude de limites asymptotes verticales et horizontales. • Exercice 3 : étude de limites de
 Dérivées II: variations et asymptotes exercices maths standard
Dérivées II: variations et asymptotes exercices maths standard
corriges/index.html. 3s - Dérivées II : variations et asymptotes. Matières. Dérivées et monotonie ; tableau de variations ; limites et asymptotes. Exercice 1.
 Chapitre 2: Limites et Asymptotes
Chapitre 2: Limites et Asymptotes
Exercice 2.6: Déterminer ED(f) et calculer les limites à gauche et à droite des valeurs interdites. 1) f (x) = 12 −2x. 3− x. 2) f (x)
 Asymptotes exercices corrigés pdf
Asymptotes exercices corrigés pdf
Limites asymptotes exercices corrigés. Limites et asymptotes exercices corrigés. Exercices corrigés sur les asymptotes. Exercices asymptotes corrigés terminale
 Limites asymptotes EXOS CORRIGES
Limites asymptotes EXOS CORRIGES
M. CUAZ http://mathscyr.free.fr. Page 1/18. LIMITES – EXERCICES CORRIGES. Exercice n°1. Déterminer la limite éventuelle en + ? de chacune des fonctions
 1 Limites et comportement asymptotique Exercices corrigés
1 Limites et comportement asymptotique Exercices corrigés
Sont abordés dans cette fiche : • Exercice 1 : détermination graphique d'une limite et d'une équation d'asymptote à une courbe. (asymptote verticale et
 Limites de fonctions et asymptotes - Exercices Fiche 2
Limites de fonctions et asymptotes - Exercices Fiche 2
Déterminer la limite de f en + et en - . 4. Montrer que la courbe C f représentative de la fonction f admet une asymptote en + et en - .
 I Exercices
I Exercices
Calculer les limites des fonctions suivantes et préciser lorsque la courbe représentative de f (notée (Cf )) admet une asymptote horizontale. 1. f(x) = x3 ?
 Limites-et-asymptotes-corriges.pdf
Limites-et-asymptotes-corriges.pdf
= ? : la droite d'équation. 5 y = ? est asymptote horizontale à la courbe représentative de f. Exercice 7 : a). 0 lim ( ) x.
 Dérivées II: variations et asymptotes exercices maths standard
Dérivées II: variations et asymptotes exercices maths standard
Lien vers la page mère : Exercices avec corrigés sur www.deleze.name Dérivées et monotonie ; tableau de variations ; limites et asymptotes. Exercice 1.
 Limites et comportement asymptotique Exercices corrigés - AlloSchool
Limites et comportement asymptotique Exercices corrigés - AlloSchool
Sont abordés dans cette fiche : • Exercice 1 : détermination graphique d'une limite et d'une équation d'asymptote à une courbe.
 Limites et asymptotes et etudes de fonctions
Limites et asymptotes et etudes de fonctions
Construire avec un tableau de variation. Pour les exercices de 1 à 4 utiliser le tableau de variations pour trouver le domaine de définition
 Chapitre 2: Limites et Asymptotes
Chapitre 2: Limites et Asymptotes
voisinage d'un trou ou d'un bord (point limite ou asymptote verticale) de son Exercice 2.3: Esquisser le graphe de la fonction f définie par f (x) = 2? ...
 Limites – Corrections des Exercices
Limites – Corrections des Exercices
Correction : On déduit de la question précédente que la droite d'équation x = 1/3 est une asymptote verticale. —. -9-. Page 10. DAEU-B – Maths.
Exercice n
o1Premiers calculs de limites.
a.Limites en+∞(quandxdevient arbitrairement grand). (a)limx→+∞2020-x (b)limx→+∞12020-x (c)limx→+∞2020-1x (d)limx→+∞3x2+ 2x3 (e)limx→+∞3x2+1x (f)limx→+∞13x2+ 1(g)limx→+∞⎷3x2+ 1 (h)limx→+∞3x 2-5x -2 (i)limx→+∞2⎷3x-5Correction :
(a)limx→+∞2020-x=-∞, carxdevient arbitrairement grand, avec un coefficient negatif.(b)limx→+∞12020-x= 0, car on divise1par2020-x, une quantité arbitrairement grande (né-
gative). (c)limx→+∞2020-1x = 2020, car1x devient arbitrairement petit.(d)limx→+∞3x2+ 2x3= +∞, car on ajoute deux quantités,3x2et2x3, qui deviennent arbitraire-
ment grandes. (e)limx→+∞3x2+1x = +∞, car on ajoute,3x2, une quantité qui deviennent arbitrairement grandes et 1x , qui devient arbitrairement petit. (f)limx→+∞13x2+ 1= 0, car on divise1par3x2+ 1, une quantité arbitrairement grande.(g)limx→+∞⎷3x2+ 1 = +∞, car on met dans la racine carrée une quantité arbitrairement grande,
donc cette racine devient elle aussi arbitrairement grande. (h)limx→+∞3x 2-5x -2 =-2car les deux quantités3x 2et5x deviennent arbitrairement petites, donc tendent vers0, et seul reste-2.(i)limx→+∞2⎷3x-5= 0, car la quantité3x-5devient arbitrairement grande, donc⎷3x-5
aussi, et donc son inverse devient arbitrairement petit. b.Limites en-∞(quandxdevient arbitrairement grand dans les négatifs). (a)limx→-∞3x2 (b)limx→-∞2020-x (c)limx→-∞2020-1x (d)limx→-∞3x2-2x3 (e)limx→-∞3x2+1x (f)limx→-∞13x2+ 1(g)limx→-∞⎷3x2+ 1 (h)limx→-∞3x 2-5x -2 (i)limx→-∞2⎷5-3xCorrection :
(a)limx→-∞3x2= +∞, carx2, et donc3x2, est positif et devient arbitrairement grand. -1-DAEU-B - MathsLimites - Corrections des ExercicesUGA 2020-2021(b)limx→-∞2020-x= +∞, carxdevient arbitrairement grand dans les négatif, et est multipliíe
par un coefficient negatif. (c)limx→-∞2020-1x = 2020, car1x devient arbitrairement petit.(d)limx→-∞3x2-2x3= +∞, car on ajoute deux quantités,3x2et-2x3, qui deviennent arbitrai-
rement grandes. (e)limx→-∞3x2+1x = +∞, car on ajoute,3x2, une quantité qui deviennent arbitrairement grandes et 1x , qui devient arbitrairement petit.(f)limx→-∞13x2+ 1= 0, car on divise1par3x2+1, une quantité arbitrairement grande (positive).
(g)limx→-∞⎷3x2+ 1 = +∞, car on met dans la racine carrée3x2+1, une quantité arbitrairement
grande, donc cette racine devient elle aussi arbitrairement grande. (h)limx→-∞3x 2-5x -2 =-2, car les deux quantités3x 2et5x deviennent arbitrairement petites, donc tendent vers0, et seul reste-2.(i)limx→-∞2⎷5-3x= 0, car la quantité5-3xdevient arbitrairement grande, donc⎷5-3x
aussi, et donc son inverse devient arbitrairement petit. c.Limites en un point (quandxtend vers une valeur finie). (a)limx→202112020-x (b)limx→13x2+1x (c)limx→1⎷3x2+ 1 2 (f)limx→23x2+ 2x3Correction :
(a)limx→23x2+ 2x3= 28, car3.22+ 2.23= 3.4 + 2.8 = 28. (b)limx→13x2+1x = 4, car3.12+ 1/1 = 4. (c)limx→1⎷3x2+ 1 = 2, car3x2+ 1tend vers3.12+ 1 = 4et⎷4 = 2. (d)limx→22⎷3x-5= 2, car3x-5tend vers3.2-5 = 1et2⎷1 = 2/1 = 1. (e)limx→202112020-x=-1, car2020-Xtend vers2020-2021 =-1. (f)limx→02-1x2= +∞, car on divise1parx2, une quantité arbitrairement grande positive.
d.Limites à gauche et à droite d"un point. (a)limx→2+12x-4 (f)limx→1-3x2+1⎷1-xCorrection :
-2-DAEU-B - MathsLimites - Corrections des ExercicesUGA 2020-2021(a)limx→2+12x-4= +∞, car2x-4tend vers0en étantpositif, donc12x-4devient arbitrairement
grand dans les positifs. (b)limx→2-12x-4=-∞, car2x-4tend vers0en étantnégatif, donc12x-4devient arbitraire- ment grand dans les négatifs. (c)limx→2+1(2x-4)4= +∞, car(2x-4)2tend vers0en étantpositif, donc1(2x-4)2devient arbitrairement grand dans les positifs. (d)limx→2-1(2x-4)4= +∞, car(2x-4)2tend vers0en étantpositif, donc1(2x-4)2devient arbitrairement grand dans les positifs. (e)limx→0+3x2+1⎷x = +∞, car3x2tend vers0, tandis que⎷xtend vers0en étantpositif, donc1⎷x
devient arbitrairement grand dans les positifs.(f)limx→1-3x2+1⎷1-x= +∞, car3x2tend vers3, tandis que⎷1-xtend vers0en étantpositif,
donc1⎷1-xdevient arbitrairement grand dans les positifs.
Exercice n
o2 Déterminer les limites suivantes aux valeurs demandées. (1).a.limx→α-2x3, pourα= 2,+∞et-∞. b.limx→α3⎷x, pourα= +∞et4.Correction :
a.limx→α-2x3, pourα= 2,+∞et-∞.Limite quandxtend vers2:
limx→2x3= 23= 8, donclimx→2-2x3=-2.8 =-16.Limite quandxtend vers+∞:
limx→+∞x3= +∞, donc, puisque-2<0, on alimx→2-2x3=-∞.Limite quandxtend vers-∞:
limx→-∞x3=-∞, donc, puisque-2<0, on alimx→2-2x3= +∞. b.limx→α3⎷x, pourα= +∞et4.Limite quandxtend vers+∞:
limx→+∞⎷x, donclimx→+∞3⎷x= +∞.Limite quandxtend vers4:
limx→4⎷x=⎷4 = 2, donclimx→43⎷x= 3.2 = 6. (2).a.limx→αx3+1x , pourα= 2,+∞et-∞. -3-DAEU-B - MathsLimites - Corrections des ExercicesUGA 2020-2021b.limx→αx3+x2, pourα= 2,+∞et-∞.
c.limx→α2x2-3x+⎷x, pourα= 2et+∞.Correction :
a.limx→αx3+1x , pourα= 2,+∞et-∞.Limite quandxtend vers2:
lim x→2x3= 23= 8etlimx→21x =12 , donclimx→2x3+1x = 8×(-12 ) =-4.Limite quandxtend vers+∞:
lim x→+∞x3= +∞etlimx→+∞1x = 0, donc on alimx→+∞x3+1xLimite quandxtend vers-∞:
lim = 0, donc on alimx→-∞x3+1x b.limx→αx3+x2, pourα= 2,+∞et-∞.Limite quandxtend vers2:
lim x→2x3= 23= 8etlimx→2x2= 4, donclimx→2x3+x2= 8 + 4 = 12.Limite quandxtend vers+∞:
lim x→+∞x3= +∞etlimx→+∞x2= +∞, donc on alimx→+∞x3+x2= +∞.Limite quandxtend vers-∞:
limx→-∞x3=-∞etlimx→-∞x2= 0, donclimx→-∞x3+x2mène à uneForme Indéterminée "∞-∞".
Pour lever cette forme indéterminée, on factorise l"expression et on utilise les règles de limite
d"un produit :x3+x2=x3(1 +1x )et puisquelimx→-∞(1 +1x ) = 1, on obtientlimx→-∞x3+x2= lim x→-∞x3(1 +1x c.limx→α2x2-3x+⎷x, pourα= 2et+∞.Limite quandxtend vers2:
limx→22x2= 2.22= 8,limx→2-3x=-3.2 =-6etlimx→2⎷x=⎷2, donclimx→22x2-3x+⎷x= 8-6+⎷2 =
2 +⎷2.
Limite quandxtend vers+∞:
limx→+∞2x2= +∞,limx→+∞-3x=-∞etlimx→+∞⎷x= +∞, donc on a uneForme Indéterminée
En factorisant parx2, on obtient2x2-3x+⎷x=x2? 2-3x +1x ⎷x . Orlimx→+∞x2= +∞et lim x→+∞? 2-3x +1x ⎷x = 2, donc on obtientlimx→+∞2x2-3x+⎷x= +∞ (3).a.limx→αx3?1x -1?, pourα= 2,+∞et-∞. -4-DAEU-B - MathsLimites - Corrections des ExercicesUGA 2020-2021b.limx→α(3x+ 2)(x2-5), pourα= 0,+∞et-∞.
c.limx→α1x (3-⎷x), pourα= 2et+∞.Correction :
a.limx→αx3?1x -1? , pourα= 2,+∞et-∞.Limite quandxtend vers2:
lim x→2x3= 23= 8etlimx→21x -1 =12 -1 =-12 , donclimx→2x3?1x -1? = 8 +12 =172Limite quandxtend vers+∞:
lim x→+∞x3= +∞etlimx→+∞1x -1 =-1, donc, puisque-1<0, on alimx→+∞x3?1x -1?Limite quandxtend vers-∞:
lim -1 =-1, donc, puisque-1<0, on alimx→-∞x3?1x -1? b.limx→α(3x+ 2)(x2-5), pourα= 0,+∞et-∞.Limite quandxtend vers0:
limx→23x+ 2 = 2etlimx→2x2-5 =-5, donclimx→2(3x+ 2)(x2-5) = 2.(-5) =-10.Limite quandxtend vers+∞:
limx→+∞3x+ 2 = +∞etlimx→+∞x2-5 =-1, donc on alimx→+∞(3x+ 2)(x2-5) = +∞.
Limite quandxtend vers-∞:
limx→-∞3x+ 2 =-∞etlimx→-∞x2-5 = +∞, donc on alimx→-∞(3x+ 2)(x2-5) =-∞.
c.limx→α1x (3-⎷x), pourα= 2et+∞.Limite quandxtend vers2:
lim x→21x =12 etlimx→23-⎷x= 3-⎷2, donclimx→21x (3-⎷x) =3-⎷2 2Limite quandxtend vers+∞:
lim x→+∞1x= 0etlimx→+∞3-⎷x=-∞1, donc on obtient uneForme Indéterminée "0× ∞".
En développant, on obtient
1x (3-⎷x) =3x -1⎷x . Orlimx→+∞3x = 0etlimx→+∞1⎷x = 0, donc on obtientlimx→+∞1x (3-⎷x) =3x -1⎷x = 0, par somme de limites. (4).a.limx→α? 1x -2?2x+ 1, pourα= 2,+∞et-∞. b.limx→α2x+ 1? 1x -2?, pourα= +∞et-∞. c.limx→α1/x2/⎷x , pourα= +∞. -5- DAEU-B - MathsLimites - Corrections des ExercicesUGA 2020-2021d.limx→α1x -2-3⎷x , pourα= +∞. e.limx→α2x2+ 3x+ 43x2+ 5, pourα= 0et+∞.Correction :
a.limx→α? 1x -2?2x+ 1, pourα= 2,+∞et-∞.Limite quandxtend vers2:
lim x→21x -2 =12 -2 =-32 etlimx→22x+ 1 = 5, donclimx→2? 1x -2?2x+ 1=-32×5-310Limite quandxtend vers+∞:
lim x→+∞1x -2 =-2etlimx→+∞2x+ 1 = +∞, donc on alimx→+∞? 1x -2?2x+ 1= 0.Limite quandxtend vers-∞:
lim x→-∞1x -2 =-2etlimx→-∞2x+ 1 =-∞, donc on alimx→-∞? 1x -2?2x+ 1= 0. b.limx→α2x+ 1? 1x -2?, pourα= +∞et-∞.Limite quandxtend vers+∞:
lim x→+∞2x+ 1 = +∞etlimx→+∞1x -2 =-2, donc, puisque-2<0, on alimx→+∞? 1x -2?2x+ 1=-∞.Limite quandxtend vers-∞:
lim x→-∞2x+ 1 =-∞etlimx→-∞1x -2 =-2, donc, puisque-2<0, on alimx→-∞? 1x -2?2x+ 1= +∞. c.limx→α1/x2/⎷x , pourα= +∞. lim x→+∞1/x= 0etlimx→-∞2/⎷x= 0, donc on obtient uneForme Indéterminée "00 ". On change donc l"expression de la fonction, en simplifiant la fraction :1/x2/⎷x
=⎷x 2x=12 ⎷xOn obtient quelimx→+∞1/x2/⎷x
= limx→+∞12 ⎷x = 0. d.limx→α1x -2-3⎷x , pourα= +∞. lim x→+∞1/x-2 =-2etlimx→-∞-3⎷x = 0. Mais pour déterminer la limite du quotient, nous devons être plus précis, et indiquer le signe du dénominateur : on a toujours ⎷x≥0, donc-3⎷x tend vers 0 : on note celalimx→-∞-3⎷x = 0-. Et par les règles de limite de quotient, on obtient : lim x→+∞1x -2-3⎷x e.limx→α2x2+ 3x+ 43x2+ 5, pourα= 0et+∞.Limite quandxtend vers0:
-6- DAEU-B - MathsLimites - Corrections des ExercicesUGA 2020-2021lim x→02x2+ 3x+ 4 = 4etlimx→03x2+ 5 = 5, donclimx→02x2+ 3x+ 43x2+ 5=45Limite quandxtend vers+∞:
limx→+∞2x2+ 3x+ 4 =-2etlimx→+∞3x2+ 5 = +∞, donc on obtient uneForme Indéterminée
". A nouveau, pour lever l"indéterminée, on change donc l"expression de la fonction; ici, l"idée
est defactoriser le numérateur et le dénominateur par la plus grand puissance dex:2x2+ 3x+ 43x2+ 5=x2(2 + 3/x+ 4/x2)x
2(3 + 5/x2)=2 + 3/x+ 4/x23 + 5/x2.
Maintenant, on alimx→+∞2 + 3/x+ 4/x2= 2etlimx→+∞3 + 5/x2= 3, don on obtient que lim x→+∞2x2+ 3x+ 43x2+ 5=23Exercice n
o3Déterminer les limites des fonctions suivantes aux valeurs demandées (en distinguant, si besoin,
les limites à gauche et à droite. a.f(x) =4x4-xen0et en4.Correction :limx→0f(x) =4.04-0=04
= 0.On alimx→4x>4(4-x) = 0-, tandis quelimx→4x<4(4-x) = 0+. Donclimx→4x>4f(x) =-∞etlimx→4x<4f(x) = +∞
(limite de quotient de fonctions). b.g(x) = 5x-1 +1x-3en+∞, en3et en-∞. Correction :On alimx→±∞1x-3= 0, donclimx→±∞g(x) =±∞.D"autre part,limx→3x>31x-3= +∞, etlimx→3x<31x-3=-∞. Donclimx→3x>3g(x) = +∞etlimx→3x<3g(x) =-∞.
c.h(x) =?⎷x-1 +1x en+∞et en0. Correction :Commençons par noter que cette fonction a pour ensemble de définition]0;+∞[. On ne cherchera donc à déterminer que la limite àdroitede0(car pourx <0, la fonction n"est pas définie). On alimx→0x>01x = +∞, Donclimx→0x>0h(x) = +∞.D"autre part,limx→+∞h(x) = +∞.
d.k(x) = (4-x2)(3x-1)en+∞, en0et en-∞.Correction :On a d"une partlimx→±∞(4-x2) =-∞etlimx→0(4-x2) = 4. D"autre part,limx→±∞(3x-
1) =±∞etlimx→0(3x-1) =-1. On a donclimx→+∞k(x) =-∞,limx→-∞k(x) = +∞etlimx→0k(x) =-4
(limite de produit de fonctions). e.l(x) =3-⎷3 x (3-⎷x)en9et en0.Correction :limx→9l(x) =3-⎷3
9 (3-⎷9) = 0.D"autre part on a3-⎷3>0etlimx→0(3-⎷x) = 3>0, donclimx→0x>0l(x) = +∞etlimx→0x<0l(x) =-∞.
-7- DAEU-B - MathsLimites - Corrections des ExercicesUGA 2020-2021- f.u(x) =4x-3(4-x)2en4.Correction :On alimx→4(4x-3) = 13>0, etlimx→4(4-x)2= 0+. Donclimx→4u(x) = +∞(limite de
quotient de fonctions). g.v(x) =x2-1/x2en+∞, en0et en-∞.Correction :Puisquelimx→±∞1x
2= 0, on alimx→±∞v(x) = limx→±∞x2= +∞.
Par ailleurs,limx→0v(x) = limx→0-1x
2=-∞.
h.w(x) =1x(x-7)en+∞, en7et en0.Correction :On alimx→+∞x(x-7) = +∞(limite d"un produit), donclimx→+∞w(x) = 0.
Puisquex >0lorsquextend vers7, et quelimx→7x>71x-7= +∞etlimx→7x<71x-7=-∞, on alimx→7x>7w(x) =
+∞etlimx→7x<7w(x) =-∞.En revanche, puisquex-7<0lorsquextend vers0, on alimx→0x>0w(x) =-∞etlimx→0x<0w(x) = +∞.
Exercice n
o4 Déterminer les limites en+∞et en-∞des fonctions suivantes. a.f(x) = 2-x-x3. Correction :On alimx→±∞x= limx→±∞x3=±∞. Donclimx→+∞f(x) =-∞et
lim x→-∞f(x) = +∞. b.g(x) =x4/2-x2/4.Correction :On a une F.I. '∞ - ∞". Mais
en factorisant :g(x) =x4(12 -14x2). Puisque lim x→±∞(12 -14x2) =12quotesdbs_dbs47.pdfusesText_47[PDF] limites et continuité cours bac pdf
[PDF] limites et continuité exercices corrigés
[PDF] limites et continuité exercices corrigés bac
[PDF] limites et continuité exercices corrigés bac maths
[PDF] limites et continuité exercices corrigés bac pdf
[PDF] limites et continuité exercices corrigés bac science
[PDF] limites et continuité exercices corrigés mpsi
[PDF] limites et continuité exercices corrigés pdf
[PDF] Limites et convexité
[PDF] Limites et étude de fonctions
[PDF] Limites et fonctions
[PDF] limites et fonctions composée
[PDF] Limites et formes indeterminées
[PDF] Limites et propriétés
