[PDF] Chapitre 7 Fonctions réciproques et nouvelles fonctions usuelles





Previous PDF Next PDF



1) Fonction reciproque 2) Propriete de la fonction reciproque

C I l'ensemble des fonctions continues et strictement monotones sur I. 1) Fonction reciproque. Theoreme : Si. ( ) m f C I.



Fonctions usuelles et réciproques Fiche de cours

L'application réciproque de ln est la fonction exponentielle c'est-à-dire. ∀x ∈ R ∀y ∈]0



Fonctions réciproques

Théorème 1 Si f est une fonction bijective continue sur un intervalle alors sa fonction réciproque f L1 est aussi continue. 11.1.5 Fonction réciproque – Graphe.



1 Fonction réciproque

D'où : Arccos/(x) = −. 1. √1. − x2. IUT de Cachan GEII2. 5. Page 6. 1.3 Arccos - Arcsin - Arctan. 1 FONCTION RÉCIPROQUE. La courbe représentative de Arccos 



Fonctions réciproques

Théor`eme 1 : Toute fonction f définie sur un intervalle I continue et strictement monotone sur cet intervalle réalise une bijection de cet intervalle I 



Composition de fonctions dérivées successives et fonction réciproque

12 oct. 2017 Exemple : Soit la fonction h définie sur ] − ∞;1] par h(x) = √1 − x. 1) Décomposer h en deux fonctions élémentaires. 2) Déterminer les ...





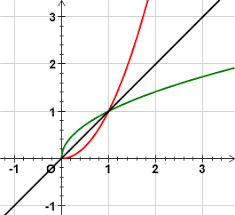Résumé : Fonctions réciproques Niveau : Bac sciences Résumé : Fonctions réciproques Niveau : Bac sciences

: Fonctions réciproques. Niveau : Bac sciences expérimentales. Réalisé par : Prof. Benjeddou Saber. Email : saberbjd2003@yahoo.fr. Soit un intervalle de ℝ et ...



Feuille dexercices 7 Fonctions trigonométriques réciproques

Fonctions trigonométriques réciproques. Exercice 1. 1. Montrer que. 0 < arccos Sur quel ensemble cette fonction est-elle définie et continue ? (Soyez ...



1) Fonction reciproque 2) Propriete de la fonction reciproque

C I l'ensemble des fonctions continues et strictement monotones sur I. 1) Fonction reciproque. Theoreme : Si. ( ) m f C I.



Fonction réciproque

Fonction réciproque. Christelle MELODELIMA VII. Fonctions logarithmes et exponentielles de base quelconque a. 1. Fonctions logarithmiques (a>0 et a ?1) ...



Fonctions réciproques

Théorème 1 Si f est une fonction bijective continue sur un intervalle alors sa fonction réciproque f L1 est aussi continue. 11.1.5 Fonction réciproque – Graphe.



Chapitre12 : Fonctions circulaires réciproques

?. MPSI Mathématiques. Analyse réelle et complexe. 3. Page 4. III. LA FONCTION Arctan. CHAPITRE 12. FONCTIONS CIRCULAIRES RÉCIPROQUES. ‚ La fonction cos est 



Chapitre 7 Fonctions réciproques et nouvelles fonctions usuelles

ln1 pxq “. 1 x . 7.2 Fonctions trigonométriques réciproques. Les fonction trigonométriques (sinus cosinus



Chapitre 2 : Fonctions rciproques

Théorème : Si f continue strictement monotone sur I alors f réalise une bijection de I sur f (I). * On note f. -1 la fonction réciproque de f.



Fonctions usuelles et réciproques Fiche de cours

L'application réciproque de ln est la fonction exponentielle c'est-à-dire. ?x ? R ?y ?]0



La réciproque f?1 dune fonction bijective f.

Nous énonçons les propriétés fondamentales de la fonction réciproque f?1 par rapport. `a la fonction f: 1. Seules les fonctions bijectives peuvent avoir une 



2.2 Graphe dune fonction numérique – définition 2.3 Réciproque

Tracé du graphe de la fonction inverse f : x ?. 1 x définie sur Df = R?. 2.3 Réciproque composition des fonctions. Définition 16 (Réciproque).



Définition : Bijection Définition : Fonction réciproque Résumé

Bac Sc. expérimentales – Résumé : Fonctions réciproques. Définition : "Bijection" Soit un intervalle de ? et une fonction définie sur .



[PDF] Fonctions réciproques

Dèfinition 1 (Fonctions réciproque) Si f est une application de X dans Y et g est une application de Y dans X telles que — f (g (y)) = y pour tout y ? Y — g 



[PDF] 1) Fonction reciproque 2) Propriete de la fonction reciproque

Exposé 65 : Fonction reciproque d'une fonction continue strictement monotone sur un intervalle de » Exemple Pre requis : - notion d'intervalle - bijection



[PDF] Fonctions réciproques

BTS MAI 2 Chap 8 : Fonctions réciproques I Définition Théor`eme 1 : Toute fonction f définie sur un intervalle I continue et strictement monotone sur



[PDF] Dérivation de fonctions réciproques

Dérivation de fonctions réciproques- Fonctions élémentaires Exercice 1: Montrer que les fonctions ƒ et g admettent une fonction réciproque que l'on



[PDF] La notion de fonction réciproque et son enseignement

Puis nous exposons quelques fonctions réciproques de références avec lesquelles travaillent les enseignants du secondaire et du post-secondaire Enfin nous



[PDF] Fonctions usuelles et réciproques Fiche de cours

Si f est une fonction bijective de E dans F alors f?1 est définie de F dans E 1 1 t dt L'application réciproque de ln est la fonction exponentielle 



[PDF] Bijection Définition : Fonction réciproque Résumé

1/4 Professeur : Benjeddou Saber Bac Sc expérimentales – Résumé : Fonctions réciproques Définition : "Bijection" Théorème :



[PDF] Fonction réciproque dune fonction strictement monotone sur un

Soit f : I ?? R une fonction continue et strictement monotone définie sur un intervalle I ? R 63 1 Fonctions réciproques Définition 1 : Soient E 



[PDF] Fonctions trigonométriques réciproques

Les fonctions sinus cosinus définies de r dans l'intervalle [-1 ;1] sont des applications surjectives par définition c'est à dire :



[PDF] Feuille 1 Fonctions réciproques & Dérivabilité Quelques Rappels

Exercice 4 En revenant à la définition donner le domaine de dérivabilité et calculer la dérivée des fonctions suivantes 1 La fonction x ?? xn définie sur R 

  • Quelle est la formule de la réciproque ?

    La relation réciproque d'une fonction f de X dans Y est la relation notée f-1, de Y dans X, telle que, pour tous les éléments du domaine de f, si y = f(x), alors x = f -1(y).

  • Quelle est la fonction réciproque ?

    En analyse, la fonction réciproque (ou bijection réciproque) d'une fonction bijective f est une fonction notée f-1 qui, à partir du résultat obtenu en appliquant f sur un nombre, redonne ce nombre.

  • Comment trouver la fonction réciproque d'une fonction ?

    La réciproque d'une fonction f s'obtient en intervertissant les valeurs de x et de y puis en isolant y . Elle se note f?1 . On obtient le graphique d'une réciproque en faisant subir à notre fonction une réflexion par rapport à l'axe y=x .
  • Afin de trouver la règle de la fonction réciproque de f, il suffit de poser x=f(y) et d'isoler la variable y. Déterminons si la fonction f(x)=(x?1)3+2 est injective. Si oui, trouvons la fonction réciproque de f. Pour toutes valeurs x1?x2, on a que (x1?1)3+2?(x2?1)3+2.

Chapitre 7

Fonctions reciproques et nouvelles

fonctions usuelles

Sommaire7.1 Fonctions Reciproques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .117

7.1.1 Denition, proprietes, premiers exemples . . . . . . . . . . . . . . . . . . . . . . . . . .

117

7.1.2 Continuite et derivabilite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

119

7.2 Fonctions trigonometriques reciproques . . . . . . . . . . . . . . . . . . . . . . . . .

120

7.2.1 Fonction arcsinus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

121

7.2.2 Fonction arccosinus . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

121

7.2.3 Fonction arctangente . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

122

7.2.4 Developpements limites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

123

7.3 Fonctions hyperboliques . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

124

7.3.1 Fonction sinus, cosinus et tangente hyperboliques . . . . . . . . . . . . . . . . . . . . .

124

7.3.2 Developpements limites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

127

7.4 Fonctions hyperboliques reciproques . . . . . . . . . . . . . . . . . . . . . . . . . . .

128

7.4.1 Fonction argument sinus hyperbolique . . . . . . . . . . . . . . . . . . . . . . . . . . .

128

7.4.2 Fonction argument cosinus hyperbolique . . . . . . . . . . . . . . . . . . . . . . . . . .

129

7.4.3 Fonction argument tangente hyperbolique . . . . . . . . . . . . . . . . . . . . . . . . .

130

7.4.4 Developpements limites . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .

131 7.1 Fonctions Reciproques

7.1.1 Denition, proprietes, premiers exemples

Denition 7.1Soientfetgdeux fonctions a valeurs reelles, denies respectivement sur des domainesDf

etDg; on dit quefetgsont reciproques l'une de l'autre si les deux conditions suivantes sont veriees :

(i)fpDfq €DgetgfId, c.-a-d. : pour toutaPDf:pgfqpaq gfpaqa; (ii)gpDgq €DfetfgId, c.-a-d. : pour toutbPDg:pfgqpbq fgpbqb; on note alorsgf1etfg1. Remarque 7.2Sifetgsont reciproques l'une de l'autre, on a alorsfpaq bsi et seulement sigpbq a;

on en deduit que les graphes des fonctionsfetgsont symetriques l'un de l'autre par rapport a la droite

yx; (cette symetrie permute les r^oles dexet dey;) cela montre egalement que la reciproque d'une fonction,

lorsqu'elle existe, est necessairement unique. m aj 28 ao^ut, 2017117Laurent Koelblen|UPMC 2017{2018 Chapitre 7. Nouvelles fonctions1M001Analyse et Algebre pour les Sciencesxy y"fpxq y"gpxq y"x

a babRemarque 7.3Sifetgsont reciproques l'une de l'autre, alors elles sont toutes les deux injectives, c.-a-d. :

tout elementde fpDfqa un unique antecedent parf; tout elementde fpDgqa un unique antecedent parg; ce qu'on traduit par les formules suivantes : p ourtout px1;x2q PDf: sifpx1q fpx2qalorsx1x2; p ourtout px1;x2q PDg: sigpx1q gpx2qalorsx1x2; en eet : si fpx1q fpx2qalorspgfqpx1q pgfqpx2q, maisgfId, d'oux1x2; si gpx1q gpx2qalorspfgqpx1q pfgqpx2q, maisfgId, d'oux1x2. Proposition 7.4Soitfune fonction a valeur reelle denie sur un domaineDf; alorsfadmet une fonction reciproque si et seulement sifest injective.

Preuve :d'apres la remarque 7.3, on sait deja que sifadmet une fonction reciproque alorsfest injective;

reciproquement, on suppose quefest injective et on denitgsurDgfpDfqen posant, pourPDg:gpbq a,

ouaest l'unique antecedent debparf; la fonctiong, ainsi denie, est reciproque de la fonctionf.Remarque 7.5Une fonctionfdenie sur un intervalleId'interieur non vide, continue et strictement mono-

tone (strictement croissante ou strictement decroissante), est injective; elle admet donc une fonction reciproque

gdenie sur l'intervalleJfpIqqui est egalement d'interieur non vide, d'apres le theoreme des valeurs intermediaires 2.65; on etudiera quelques exemples de cette nature dans la suite de ce chapitre. Exemple 7.6(1)La fonction iden tited eniesur Rparfpxq xest sa propre reciproque; (2) la fonction racine carr eed enies urRpargpyq ?yn'est pas la reciproque de la fonction carree denie surRparfpxq x2; on a biengpDgq €Dfet pour toutyPR:pfgqpyq y; on a egalement fpDfq €Dget pour toutxPR:pgfqpxq x, mais pourxPR:pgfqpxq x; on aurait d'ailleurs

pu faire immediatement la remarque que la fonctionfpxq x2n'est pas injective, et qu'elle ne peut donc

avoir de fonction reciproque; xy y"x2 y"?xUPMC 2017{2018|Laurent Koelblen118maj 28 ao^ut, 2017

1M001Analyse et Algebre pour les Sciences Chapitre 7. Nouvelles fonctions(3)toutefois, la fonction racine carr eeest la r eciproquede la fonction carr eerestrein te aR.xy

y"x2

y"?xOn a introduit la fonction logarithme au chapitre 3, sans en donner la denition. On est a present en mesure

de la faire.

Denition 7.7

xy

1 2e e212ee

2 y"exppxq y"lnpxqLa fonction exponentielle est strictement croissante deRsurR; sa fonction reciproque est appelee logarithme et est notee ln; elle est denie surR. xy

1 2e e212ee

2 y"exppxq y"lnpxq7.1.2 Continuite et derivabilite Theoreme 7.8Soitfune fonction denie sur un intervalleId'interieur non vide, continue et strictement

monotone, et soitgsa fonction reciproque denie surJfpIq, qui est egalement un intervalle d'interieur non

vide, d'apres le theoreme des valeurs intermediaires 2.65; alors : (a)gest strictement monotone surJet de m^eme sens de variation quef; (b)gest continue surJ; (c) si fpxqest derivable enxaet sif1paq 0, alorsgpyqest derivable enybfpaqet on ag1pbq 1f 1paq; (d) si fest derivable surIet sif1ne s'annule pas surI, alorsgest derivable surJet on ag11f

1gc.-a-d. :

f111f 1f1: Preuve :(a)soit py1;y2q PJ2tels quey1 y2et soitx1gpy1qetx2gpy2q; on a alorsy1fpx1qety2fpx2q; si

fest strictement croissante et six1¥x2alorsy1¥y2, ce qui est faux, doncx1 x2, ce qui montre que

est faux, doncx1¡x2, ce qui montre quegest strictement decroissante; (b) soien tbPJetagpbq; on va supposer tout d'abord queaest interieur aI, c.-a-d. qu'il existe"0¡0 tel quesa"0;a"0r €I; soit alors"¡0 tel que" "0; on a donc : aP sa";a"r € sa"0;a"0r €I d'ou : bfpaq Pfsa";a"r€J; m aj 28 ao^ut, 2017119Laurent Koelblen|UPMC 2017{2018 Chapitre 7. Nouvelles fonctions1M001Analyse et Algebre pour les Sciencesor : f sa";a"r# fpa"q;fpa"qsifest croissantefpa"q;fpa"qsifest decroissante on considere alorsmin!bfpa"q;bfpa"q) si bien que : sb;br €fsa";a"r d'ou : gsb;br€ sa";a"r; on a ainsi montre que : @"¡0 :D¡0 :@yPJ:|yb| ñgpyq gpbq " c.-a-d. quegpyqest continue enyb; siaminpIqon raisonne de la m^eme maniere en remplacant : les intervalles :sa"0;a"0r sa";a"rfpa"q;fpa"qsb;br sifest croissante, par :ra;a"0r ra;a"rfpaq;fpa"qrb;br sifest decroissante, par :ra;a"0r ra;a"rfpa"q;fpaqsb;bs avecbfpa"q et siamaxpIq, en remplacant : les intervalles :sa"0;a"0r sa";a"rfpa"q;fpa"qsb;br sifest croissante, par :sa"0;as sa";asfpa"q;fpaqsb;bs sifest decroissante, par :sa"0;as sa";asfpaq;fpa"qrb;br avecbfpa"q (c) soit bPJetyPJtel queyb; on posebpyq gpyq gpbqyb; soient alorsagpbqetxgpyq; on a bpyq xafpxq fpaq; lorsqueytend versb,xgpyqa pour limitea, cargest continue surJ, donc par composition des limites,bpyqa pour limite1f

1paq, ce qui montre quegpyqest derivable enybet que

g

1pbq 1f

1paq1pf1f1qpbq;

(d)

ce dernier p ointr esultedirectemen tdu p ointpr ecedent.Exemple 7.9la fonction logarithme etant denie comme reciproque de la fonction exponentielle qui est

derivable surR, on en deduit qu'elle est derivable sur son domaine de denitionRet que : ln

1pxq 1exp

1lnpxq

or exp

1pxq exppxqet explnpxqxd'ou :

ln

1pxq 1x

7.2 Fonctions trigonometriques reciproques

Les fonction trigonometriques (sinus, cosinus, tangente) ne sont pas injectives; elles n'admettent donc pas de

fonction reciproques; on peut toutefois proceder comme dans l'exemple 7.6 en les restreignant a des intervalles

sur lesquels elles sont strictement monotones, donc injectives. UPMC 2017{2018|Laurent Koelblen120maj 28 ao^ut, 2017

1M001Analyse et Algebre pour les Sciences Chapitre 7. Nouvelles fonctions7.2.1 Fonction arcsinus

Denition 7.10La restriction de la fonction sinus a l'intervalle 2 ;2 est strictement croissante et on a sin 2 ;2 r1;1s; elle admet donc une fonction reciproque denie surr1;1s, qui est appelee arcsinus et notee arcsin.Oxy 1

π2´1´π

21π

2 ´1 2 y"arcsinpxq

y"sinpxqProposition 7.11La fonction arcsinus est impaire, continue surr1;1set strictement croissante; elle est

derivable surs1;1ret sa derivee est : arcsin

1pxq 1?1x2;

elle est donc de classeC8surs1;1r.

Preuve :

Oxy 1

π2´1´π

21π

2 ´1 2 y"arcsinpxq

y"sinpxqd'apres le theoreme 7.8, la fonction arcsinus est continue surr1;1set strictement croissante car

la restriction de la fonction sinus a l'intervalle 2 ;2 l'est; elle est impaire pour la m^eme raison; toujours d'apres le theoreme 7.8, elle est derivable surs1;1ret sa derivee est : arcsin

1pxq 1sin

1parcsinxq1cosparcsinxq

on posetarcsinpxq; on a alorstP 2 ;2 d'ou cosptq ¥0; de pluspcostq2 psintq21; on en deduit que cosptq a1 psintq2a1x2, d'ou : arcsin

1pxq 1?1x2:

De plus, arcsin

1pxqest de classeC8car composee de fonctions de classeC8, donc arcsinpxqest de classeC8.7.2.2 Fonction arccosinus

Denition 7.12La restriction de la fonction cosinus a l'intervaller0;sest strictement decroissante et on a

cosr0;s r1;1s; elle admet donc une fonction reciproque denie surr1;1s, qui est appelee arccosinus et notee arccos. m aj 28 ao^ut, 2017121Laurent Koelblen|UPMC 2017{2018 Chapitre 7. Nouvelles fonctions1M001Analyse et Algebre pour les SciencesOxy 1

π2π´11

2π ´1 y"arccospxq

y"cospxqProposition 7.13La fonction arccosinus est continue surr1;1set strictement decroissante; elle est derivable

surs1;1ret sa derivee est : arccos

1pxq 1?1x2;

elle est donc de classeC8surs1;1r.

Preuve :d'apres le theoreme 7.8, la fonction arccosinus est continue surr1;1set strictement decroissante car

la restriction de la fonction cosinus a l'intervaller1;1sl'est; toujours d'apres le theoreme 7.8, elle est derivable

surs1;1ret sa derivee est : arccos

1pxq 1cos

1parccosxq1sinparccosxq

on posetarccospxq; on a alorstP r0;sd'ou sinptq ¥0; de pluspcostq2 psintq21; on en deduit que sinptq a1 pcostq2a1x2, d'ou : arccos

1pxq 1?1x2:

De plus, arccos

quotesdbs_dbs16.pdfusesText_22
[PDF] séquence pierre et le loup cycle 2

[PDF] trouver la fonction réciproque d'un polynome

[PDF] fonction réciproque exercices corrigés

[PDF] séquence pierre et le loup cycle 3

[PDF] fonction réciproque définition

[PDF] réciproque d'une fonction racine carré

[PDF] pierre et le loup cm2

[PDF] calcul fonction reciproque en ligne

[PDF] fonction réciproque dérivée

[PDF] activité réciproque du théorème de pythagore

[PDF] musique de film youtube

[PDF] pythagore 3eme exercices

[PDF] activité 2nd degré

[PDF] recherche musique de film

[PDF] musique de film compositeur