1) Fonction reciproque 2) Propriete de la fonction reciproque
C I l'ensemble des fonctions continues et strictement monotones sur I. 1) Fonction reciproque. Theoreme : Si. ( ) m f C I.
Fonctions usuelles et réciproques Fiche de cours
L'application réciproque de ln est la fonction exponentielle c'est-à-dire. ∀x ∈ R ∀y ∈]0
Fonctions réciproques
Théorème 1 Si f est une fonction bijective continue sur un intervalle alors sa fonction réciproque f L1 est aussi continue. 11.1.5 Fonction réciproque – Graphe.
1 Fonction réciproque
D'où : Arccos/(x) = −. 1. √1. − x2. IUT de Cachan GEII2. 5. Page 6. 1.3 Arccos - Arcsin - Arctan. 1 FONCTION RÉCIPROQUE. La courbe représentative de Arccos
Fonctions réciproques
Théor`eme 1 : Toute fonction f définie sur un intervalle I continue et strictement monotone sur cet intervalle réalise une bijection de cet intervalle I
Composition de fonctions dérivées successives et fonction réciproque
12 oct. 2017 Exemple : Soit la fonction h définie sur ] − ∞;1] par h(x) = √1 − x. 1) Décomposer h en deux fonctions élémentaires. 2) Déterminer les ...
Chapitre 7 Fonctions réciproques et nouvelles fonctions usuelles
ln1 pxq “. 1 x . 7.2 Fonctions trigonométriques réciproques. Les fonction trigonométriques (sinus cosinus
Tableaux des dérivées et primitives et quelques formules en prime
%20d%C3%A9riv%C3%A9es
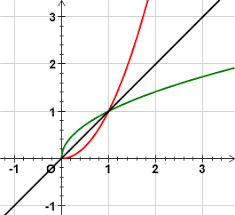Résumé : Fonctions réciproques Niveau : Bac sciences
: Fonctions réciproques. Niveau : Bac sciences expérimentales. Réalisé par : Prof. Benjeddou Saber. Email : saberbjd2003@yahoo.fr. Soit un intervalle de ℝ et ...
Feuille dexercices 7 Fonctions trigonométriques réciproques
Fonctions trigonométriques réciproques. Exercice 1. 1. Montrer que. 0 < arccos Sur quel ensemble cette fonction est-elle définie et continue ? (Soyez ...
1) Fonction reciproque 2) Propriete de la fonction reciproque
C I l'ensemble des fonctions continues et strictement monotones sur I. 1) Fonction reciproque. Theoreme : Si. ( ) m f C I.
Fonction réciproque
Fonction réciproque. Christelle MELODELIMA VII. Fonctions logarithmes et exponentielles de base quelconque a. 1. Fonctions logarithmiques (a>0 et a ?1) ...
Fonctions réciproques
Théorème 1 Si f est une fonction bijective continue sur un intervalle alors sa fonction réciproque f L1 est aussi continue. 11.1.5 Fonction réciproque – Graphe.
Chapitre12 : Fonctions circulaires réciproques
?. MPSI Mathématiques. Analyse réelle et complexe. 3. Page 4. III. LA FONCTION Arctan. CHAPITRE 12. FONCTIONS CIRCULAIRES RÉCIPROQUES. ‚ La fonction cos est
Chapitre 7 Fonctions réciproques et nouvelles fonctions usuelles
ln1 pxq “. 1 x . 7.2 Fonctions trigonométriques réciproques. Les fonction trigonométriques (sinus cosinus
Chapitre 2 : Fonctions rciproques
Théorème : Si f continue strictement monotone sur I alors f réalise une bijection de I sur f (I). * On note f. -1 la fonction réciproque de f.
Fonctions usuelles et réciproques Fiche de cours
L'application réciproque de ln est la fonction exponentielle c'est-à-dire. ?x ? R ?y ?]0
La réciproque f?1 dune fonction bijective f.
Nous énonçons les propriétés fondamentales de la fonction réciproque f?1 par rapport. `a la fonction f: 1. Seules les fonctions bijectives peuvent avoir une
2.2 Graphe dune fonction numérique – définition 2.3 Réciproque
Tracé du graphe de la fonction inverse f : x ?. 1 x définie sur Df = R?. 2.3 Réciproque composition des fonctions. Définition 16 (Réciproque).
Définition : Bijection Définition : Fonction réciproque Résumé
Bac Sc. expérimentales – Résumé : Fonctions réciproques. Définition : "Bijection" Soit un intervalle de ? et une fonction définie sur .
[PDF] Fonctions réciproques
Dèfinition 1 (Fonctions réciproque) Si f est une application de X dans Y et g est une application de Y dans X telles que — f (g (y)) = y pour tout y ? Y — g
[PDF] 1) Fonction reciproque 2) Propriete de la fonction reciproque
Exposé 65 : Fonction reciproque d'une fonction continue strictement monotone sur un intervalle de » Exemple Pre requis : - notion d'intervalle - bijection
[PDF] Fonctions réciproques
BTS MAI 2 Chap 8 : Fonctions réciproques I Définition Théor`eme 1 : Toute fonction f définie sur un intervalle I continue et strictement monotone sur
[PDF] Dérivation de fonctions réciproques
Dérivation de fonctions réciproques- Fonctions élémentaires Exercice 1: Montrer que les fonctions ƒ et g admettent une fonction réciproque que l'on
[PDF] La notion de fonction réciproque et son enseignement
Puis nous exposons quelques fonctions réciproques de références avec lesquelles travaillent les enseignants du secondaire et du post-secondaire Enfin nous
[PDF] Fonctions usuelles et réciproques Fiche de cours
Si f est une fonction bijective de E dans F alors f?1 est définie de F dans E 1 1 t dt L'application réciproque de ln est la fonction exponentielle
[PDF] Bijection Définition : Fonction réciproque Résumé
1/4 Professeur : Benjeddou Saber Bac Sc expérimentales – Résumé : Fonctions réciproques Définition : "Bijection" Théorème :
[PDF] Fonction réciproque dune fonction strictement monotone sur un
Soit f : I ?? R une fonction continue et strictement monotone définie sur un intervalle I ? R 63 1 Fonctions réciproques Définition 1 : Soient E
[PDF] Fonctions trigonométriques réciproques
Les fonctions sinus cosinus définies de r dans l'intervalle [-1 ;1] sont des applications surjectives par définition c'est à dire :
[PDF] Feuille 1 Fonctions réciproques & Dérivabilité Quelques Rappels
Exercice 4 En revenant à la définition donner le domaine de dérivabilité et calculer la dérivée des fonctions suivantes 1 La fonction x ?? xn définie sur R
Quelle est la formule de la réciproque ?
La relation réciproque d'une fonction f de X dans Y est la relation notée f-1, de Y dans X, telle que, pour tous les éléments du domaine de f, si y = f(x), alors x = f -1(y).Quelle est la fonction réciproque ?
En analyse, la fonction réciproque (ou bijection réciproque) d'une fonction bijective f est une fonction notée f-1 qui, à partir du résultat obtenu en appliquant f sur un nombre, redonne ce nombre.Comment trouver la fonction réciproque d'une fonction ?
La réciproque d'une fonction f s'obtient en intervertissant les valeurs de x et de y puis en isolant y . Elle se note f?1 . On obtient le graphique d'une réciproque en faisant subir à notre fonction une réflexion par rapport à l'axe y=x .- Afin de trouver la règle de la fonction réciproque de f, il suffit de poser x=f(y) et d'isoler la variable y. Déterminons si la fonction f(x)=(x?1)3+2 est injective. Si oui, trouvons la fonction réciproque de f. Pour toutes valeurs x1?x2, on a que (x1?1)3+2?(x2?1)3+2.
Pre requis :
- notion d"intervalle - bijection - continuité et derivabilité d"une fonction - theoreme des valeurs intermediaires dans tout l"exposé, I designe un intervalle non vide de ?. On note( )mC Il"ensemble des fonctions continues et strictement monotones sur I.1) Fonction reciproque
Theoreme : Si ( )mf C I? alors f realise une bijection sur ( )f IPreuve :
( )f I est un intervalle d"apres le theoreme des valeurs intermédiaires : ( )f I f I→ est surjective par construction Soit 21 2( , )x x I?, supposons fstrictement croissante (on change le sens des inegalité si elle
est strictement decroissante, ou on considere f-qui sera alors strictement croissante)1 2 1 2( ) ( )x x f x f x< ? Definition : Soit
( )mf C I?. L"application qui a tout ( )y f I? associe son unique antecedent par la fonction f est appelée fonction reciproque de f. On la note 1f- Remarque :
1( )( )
y f xx f y x Iy f I Si ( )mf C I? alors 1 If f Id-=? et1
( )f If f Id-=? Preuve (si le jury le demande)
, ( )x I y f I? ?tel que 1( ); ( )y f x x f y-= = 1 1 1( ) ( )If f x f y x f f Id- - -= = ? =? ?
2) Propriete de la fonction reciproque
a) Sens de variation Proposition : Si ( )mf C I? alors 1f- est strictement monotone sur ( )f I et a le même sens de variation que f. Preuve : cas où f est strictement croissante sur I Soient
2 1 2( , ) ( ( ))y y f I? tel que 1 2y y<. On pose 1 1 2 2( ), ( )x f y x f y= =
1 1 1 2 1 2 1 2 1 2( ) ( ) ( ) ( )y y f x f x x x f y f y- -< ? < ? < ? <
L"implication du milieu vient du fait que
f est croissante donc 1 2 1 2( ) ( )x x f x f x< ? < or si on prend la contraposé on a b) Continuité Lemme : Soit ( )mf C I?.( )f I est un intervalle si et seulement si f est continue sur I. Preuve : cela vient du fais que l"image d"un compact par une fonction continue est un compact. Propriété : Si
( )mf C I? alors 1f- est continue sur ( )f I. Preuve ( à faire) :
fest continue et strictement monotone sur I donc fest bijective de I sur ( )f I. fcontinue implique ( )J f I=est un intervalle, or 1f- existe et est strictment monotone d"où 1( )f J I-=, intervalle, ce qui entraine 1f-continue.
Exemple :
[ ], 1,1:2 2 sinf x x c) Dérivabilité Theoreme : Soit ( )mf C I? et ox I? tel que f soit derivable en ox et "( ) 0of x≠ Alors 1f- est dérivable en ( )o oy f x=et on a 1 11 1( )"( )
"( ) "( ( ))o o of yf x f f y Remarque : il se peut que
f ne soit pas derivable en un point et que 1f-le soit. Sur le graphe f aura une tangente verticale, et donc 1f-une tangente horizontale. Preuve (du theoreme) :
Montrons que
1 1( ) ( )1lim , "( ) 0"( )o
o oy yo of y f yf xy y f x- - La fonction
f étant dérivable en ox, on a ( ) ( )"( ) lim o o ox xof x f xf xx x -=-, comme 1f- est continue en oy, le théoreme de compositions de limites donne : 1 1 1 1( ( )) ( )"( ) lim lim
( ) ( ) ( )oo o o ox x y y oo f f y f x y yf x f y x f y f y Cette limite etant supposée non nulle, d"apres le theoreme de l"inverse d"une limite,on a (en fait c"est le theoreme des compositions de fonction avec la fonction inverse, sur un point non nul donc ou la fonction onverse est definie) 1 1( ) ( )1lim , "( ) 0"( )o
o oy yo of y f yf xy y f x- - Exemple :
2 21 1 1(arctan )"1 1 tan (tan )"
tan arctanx x y y y x y x= = = d) Graphe Soit ( )mf C I?
Graphe de
f :={}( , ( );fG x f x x I= ? Graphe de
1f- := {}{}1
1( , ( )); ( ) ( ( ), );fG y f y y f I f x x x I-
1fG- est donc le symetrique de fG par rapport à la 1ere bissectrice
Dessin
3) Exemple
a) Fonction exponentielle et logarithme neperien. exp:? +→? ?exp est continue et strictmenent monotone sur ? exp( ) Elle admet une fonction reciproque qui est ln:
( , ) ( , ln )xx e y y x y? dessin b) Fonction tangente et arctangente tan: ,2 2π π? ?- →? ?? ??, tan est continue et strictement monotone sur cet intervalle. tan ,2 2π π( )? ?- =( )? ?? ?( )?, elle admet donc une fonction reciproque notée arctan. arctan: ,2 2 ( ), ,tan ,arctan2 2x x y y y xπ π( )? ?? ? - = ? ? ? =( )? ?? ?( )? dessinquotesdbs_dbs16.pdfusesText_22
Definition : Soit
( )mf C I?. L"application qui a tout ( )y f I? associe son unique antecedent par la fonction f est appelée fonction reciproque de f. On la note 1f-Remarque :
1( )( )
y f xx f y x Iy f I Si ( )mf C I? alors 1If f Id-=? et1
( )f If f Id-=?Preuve (si le jury le demande)
, ( )x I y f I? ?tel que 1( ); ( )y f x x f y-= =1 1 1( ) ( )If f x f y x f f Id- - -= = ? =? ?
2) Propriete de la fonction reciproque
a) Sens de variation Proposition : Si ( )mf C I? alors 1f- est strictement monotone sur ( )f I et a le même sens de variation que f. Preuve : cas où f est strictement croissante sur ISoient
21 2( , ) ( ( ))y y f I? tel que 1 2y y<. On pose 1 1 2 2( ), ( )x f y x f y= =
1 11 2 1 2 1 2 1 2( ) ( ) ( ) ( )y y f x f x x x f y f y- -< ? < ? < ? <
L"implication du milieu vient du fait que
f est croissante donc 1 2 1 2( ) ( )x x f x f x< ? < or si on prend la contraposé on a b) Continuité Lemme : Soit ( )mf C I?.( )f I est un intervalle si et seulement si f est continue sur I. Preuve : cela vient du fais que l"image d"un compact par une fonction continue est un compact.Propriété : Si
( )mf C I? alors 1f- est continue sur ( )f I.Preuve ( à faire) :
fest continue et strictement monotone sur I donc fest bijective de I sur ( )f I. fcontinue implique ( )J f I=est un intervalle, or 1f- existe et est strictment monotone d"où1( )f J I-=, intervalle, ce qui entraine 1f-continue.
Exemple :
[ ], 1,1:2 2 sinf x x c) Dérivabilité Theoreme : Soit ( )mf C I? et ox I? tel que f soit derivable en ox et "( ) 0of x≠ Alors 1f- est dérivable en ( )o oy f x=et on a 111 1( )"( )
"( ) "( ( ))o o of yf x f f yRemarque : il se peut que
f ne soit pas derivable en un point et que 1f-le soit. Sur le graphe f aura une tangente verticale, et donc 1f-une tangente horizontale.Preuve (du theoreme) :
Montrons que
1 1( ) ( )1lim , "( ) 0"( )o
o oy yo of y f yf xy y f x- -La fonction
f étant dérivable en ox, on a ( ) ( )"( ) lim o o ox xof x f xf xx x -=-, comme 1f- est continue en oy, le théoreme de compositions de limites donne : 11 1 1( ( )) ( )"( ) lim lim
( ) ( ) ( )oo o o ox x y y oo f f y f x y yf x f y x f y f y Cette limite etant supposée non nulle, d"apres le theoreme de l"inverse d"une limite,on a (en fait c"est le theoreme des compositions de fonction avec la fonction inverse, sur un point non nul donc ou la fonction onverse est definie)1 1( ) ( )1lim , "( ) 0"( )o
o oy yo of y f yf xy y f x- -Exemple :
2 21 1 1(arctan )"1 1 tan (tan )"
tan arctanx x y y y x y x= = = d) GrapheSoit ( )mf C I?
Graphe de
f :={}( , ( );fG x f x x I= ?Graphe de
1f- := {}{}1
1( , ( )); ( ) ( ( ), );fG y f y y f I f x x x I-
1fG- est donc le symetrique de fG par rapport à la 1ere bissectrice
Dessin
3) Exemple
a) Fonction exponentielle et logarithme neperien. exp:? +→? ?exp est continue et strictmenent monotone sur ? exp( )Elle admet une fonction reciproque qui est ln:
( , ) ( , ln )xx e y y x y? dessin b) Fonction tangente et arctangente tan: ,2 2π π? ?- →? ?? ??, tan est continue et strictement monotone sur cet intervalle. tan ,2 2π π( )? ?- =( )? ?? ?( )?, elle admet donc une fonction reciproque notée arctan. arctan: ,2 2 ( ), ,tan ,arctan2 2x x y y y xπ π( )? ?? ? - = ? ? ? =( )? ?? ?( )? dessinquotesdbs_dbs16.pdfusesText_22[PDF] trouver la fonction réciproque d'un polynome
[PDF] fonction réciproque exercices corrigés
[PDF] séquence pierre et le loup cycle 3
[PDF] fonction réciproque définition
[PDF] réciproque d'une fonction racine carré
[PDF] pierre et le loup cm2
[PDF] calcul fonction reciproque en ligne
[PDF] fonction réciproque dérivée
[PDF] activité réciproque du théorème de pythagore
[PDF] musique de film youtube
[PDF] pythagore 3eme exercices
[PDF] activité 2nd degré
[PDF] recherche musique de film
[PDF] musique de film compositeur
