1) Fonction reciproque 2) Propriete de la fonction reciproque
C I l'ensemble des fonctions continues et strictement monotones sur I. 1) Fonction reciproque. Theoreme : Si. ( ) m f C I.
Fonctions usuelles et réciproques Fiche de cours
L'application réciproque de ln est la fonction exponentielle c'est-à-dire. ∀x ∈ R ∀y ∈]0
Fonctions réciproques
Théorème 1 Si f est une fonction bijective continue sur un intervalle alors sa fonction réciproque f L1 est aussi continue. 11.1.5 Fonction réciproque – Graphe.
1 Fonction réciproque
D'où : Arccos/(x) = −. 1. √1. − x2. IUT de Cachan GEII2. 5. Page 6. 1.3 Arccos - Arcsin - Arctan. 1 FONCTION RÉCIPROQUE. La courbe représentative de Arccos
Fonctions réciproques
Théor`eme 1 : Toute fonction f définie sur un intervalle I continue et strictement monotone sur cet intervalle réalise une bijection de cet intervalle I
Composition de fonctions dérivées successives et fonction réciproque
12 oct. 2017 Exemple : Soit la fonction h définie sur ] − ∞;1] par h(x) = √1 − x. 1) Décomposer h en deux fonctions élémentaires. 2) Déterminer les ...
Chapitre 7 Fonctions réciproques et nouvelles fonctions usuelles
ln1 pxq “. 1 x . 7.2 Fonctions trigonométriques réciproques. Les fonction trigonométriques (sinus cosinus
Tableaux des dérivées et primitives et quelques formules en prime
%20d%C3%A9riv%C3%A9es
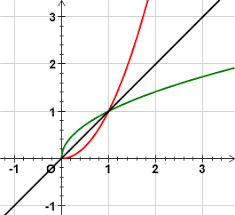Résumé : Fonctions réciproques Niveau : Bac sciences
: Fonctions réciproques. Niveau : Bac sciences expérimentales. Réalisé par : Prof. Benjeddou Saber. Email : saberbjd2003@yahoo.fr. Soit un intervalle de ℝ et ...
Feuille dexercices 7 Fonctions trigonométriques réciproques
Fonctions trigonométriques réciproques. Exercice 1. 1. Montrer que. 0 < arccos Sur quel ensemble cette fonction est-elle définie et continue ? (Soyez ...
1) Fonction reciproque 2) Propriete de la fonction reciproque
C I l'ensemble des fonctions continues et strictement monotones sur I. 1) Fonction reciproque. Theoreme : Si. ( ) m f C I.
Fonction réciproque
Fonction réciproque. Christelle MELODELIMA VII. Fonctions logarithmes et exponentielles de base quelconque a. 1. Fonctions logarithmiques (a>0 et a ?1) ...
Fonctions réciproques
Théorème 1 Si f est une fonction bijective continue sur un intervalle alors sa fonction réciproque f L1 est aussi continue. 11.1.5 Fonction réciproque – Graphe.
Chapitre12 : Fonctions circulaires réciproques
?. MPSI Mathématiques. Analyse réelle et complexe. 3. Page 4. III. LA FONCTION Arctan. CHAPITRE 12. FONCTIONS CIRCULAIRES RÉCIPROQUES. ‚ La fonction cos est
Chapitre 7 Fonctions réciproques et nouvelles fonctions usuelles
ln1 pxq “. 1 x . 7.2 Fonctions trigonométriques réciproques. Les fonction trigonométriques (sinus cosinus
Chapitre 2 : Fonctions rciproques
Théorème : Si f continue strictement monotone sur I alors f réalise une bijection de I sur f (I). * On note f. -1 la fonction réciproque de f.
Fonctions usuelles et réciproques Fiche de cours
L'application réciproque de ln est la fonction exponentielle c'est-à-dire. ?x ? R ?y ?]0
La réciproque f?1 dune fonction bijective f.
Nous énonçons les propriétés fondamentales de la fonction réciproque f?1 par rapport. `a la fonction f: 1. Seules les fonctions bijectives peuvent avoir une
2.2 Graphe dune fonction numérique – définition 2.3 Réciproque
Tracé du graphe de la fonction inverse f : x ?. 1 x définie sur Df = R?. 2.3 Réciproque composition des fonctions. Définition 16 (Réciproque).
Définition : Bijection Définition : Fonction réciproque Résumé
Bac Sc. expérimentales – Résumé : Fonctions réciproques. Définition : "Bijection" Soit un intervalle de ? et une fonction définie sur .
[PDF] Fonctions réciproques
Dèfinition 1 (Fonctions réciproque) Si f est une application de X dans Y et g est une application de Y dans X telles que — f (g (y)) = y pour tout y ? Y — g
[PDF] 1) Fonction reciproque 2) Propriete de la fonction reciproque
Exposé 65 : Fonction reciproque d'une fonction continue strictement monotone sur un intervalle de » Exemple Pre requis : - notion d'intervalle - bijection
[PDF] Fonctions réciproques
BTS MAI 2 Chap 8 : Fonctions réciproques I Définition Théor`eme 1 : Toute fonction f définie sur un intervalle I continue et strictement monotone sur
[PDF] Dérivation de fonctions réciproques
Dérivation de fonctions réciproques- Fonctions élémentaires Exercice 1: Montrer que les fonctions ƒ et g admettent une fonction réciproque que l'on
[PDF] La notion de fonction réciproque et son enseignement
Puis nous exposons quelques fonctions réciproques de références avec lesquelles travaillent les enseignants du secondaire et du post-secondaire Enfin nous
[PDF] Fonctions usuelles et réciproques Fiche de cours
Si f est une fonction bijective de E dans F alors f?1 est définie de F dans E 1 1 t dt L'application réciproque de ln est la fonction exponentielle
[PDF] Bijection Définition : Fonction réciproque Résumé
1/4 Professeur : Benjeddou Saber Bac Sc expérimentales – Résumé : Fonctions réciproques Définition : "Bijection" Théorème :
[PDF] Fonction réciproque dune fonction strictement monotone sur un
Soit f : I ?? R une fonction continue et strictement monotone définie sur un intervalle I ? R 63 1 Fonctions réciproques Définition 1 : Soient E
[PDF] Fonctions trigonométriques réciproques
Les fonctions sinus cosinus définies de r dans l'intervalle [-1 ;1] sont des applications surjectives par définition c'est à dire :
[PDF] Feuille 1 Fonctions réciproques & Dérivabilité Quelques Rappels
Exercice 4 En revenant à la définition donner le domaine de dérivabilité et calculer la dérivée des fonctions suivantes 1 La fonction x ?? xn définie sur R
Quelle est la formule de la réciproque ?
La relation réciproque d'une fonction f de X dans Y est la relation notée f-1, de Y dans X, telle que, pour tous les éléments du domaine de f, si y = f(x), alors x = f -1(y).Quelle est la fonction réciproque ?
En analyse, la fonction réciproque (ou bijection réciproque) d'une fonction bijective f est une fonction notée f-1 qui, à partir du résultat obtenu en appliquant f sur un nombre, redonne ce nombre.Comment trouver la fonction réciproque d'une fonction ?
La réciproque d'une fonction f s'obtient en intervertissant les valeurs de x et de y puis en isolant y . Elle se note f?1 . On obtient le graphique d'une réciproque en faisant subir à notre fonction une réflexion par rapport à l'axe y=x .- Afin de trouver la règle de la fonction réciproque de f, il suffit de poser x=f(y) et d'isoler la variable y. Déterminons si la fonction f(x)=(x?1)3+2 est injective. Si oui, trouvons la fonction réciproque de f. Pour toutes valeurs x1?x2, on a que (x1?1)3+2?(x2?1)3+2.
Fonctions trigonométriques réciproques
1 Définitions
Les fonctions sinus, cosinus définies de dans l'intervalle [-1 ;1] sont des applications surjectives par définition,
c'est à dire : y [-1 ;1], x tel que sin(x) = y et cos(x) = y .La fonction tangente définie de - {x x =
2 + k , k } dans est une application surjective par définition .A condition de restreindre judicieusement leurs ensembles de définition, on peut définir des fonctions qui sont
injectives et par conséquent bijectives. Pour la fonction sinus, on restreint son domaine de définition à l'intervalle [- 2 2 ] et on a : sin : [- 2 2 ] [-1 ;1] x sin(x) Alors cette fonction " sin " est bijective et on peut définir sa fonction réciproque appelée arc sinus ainsi : arcsin : [-1;1] [- 2 2 x arcsin(x) avec l'équivalence : y = arcsin(x) x = sin(y)La représentation graphique
1 f d'une fonction f -1 réciproque d'une applicatio bijective est toujours symétrique de f par rapport à la bissectrice d du premier et troisième quadrant d'équation d : y = x . 1 f f 2 Pour la fonction cosinus, on restreint son domaine de définition à l'intervalle [0 ;] et on a : cos : [0 ;] [-1 ;1] x cos(x) Alors cette fonction "cos" est bijective et on peut définir sa fonction réciproque appelée arc cosinus ainsi : arccos : [-1;1] [0 ;] x arccos(x) avec l'équivalence : y = arccos(x) x = cos(y) Pour la fonction tangente, on restreint son domaine de définition à l'intervalle ]- 2 2 [ et on a : tan : ]- 2 2 x tan(x) Alors cette fonction "tan" est bijective et on peut définir sa fonction réciproque appelée arc tangente ainsi : arctan : ]- 2 2 x arctan(x) avec l'équivalence : y = arctan(x) x = tan(y)Exemples : arcsin(1) =
2 , car sin( 2 ) = 1 arccos( 213 , car cos( 3 21
; arctan(-1) = - 4 , car tan(- 4 ) = -1
2 Remarques :
1) Soit f : A B une application bijective et f
-1 : B A sa réciproque avec y = f -1 (x) x = f(y) .On a alors : f
of -1 = id B et f -1 of = id A , c'est à dire : xB , : fof -1 (x)= id B (x) = x et yA , : f -1 of(y)= id A (y) = y . Ainsi : x [-1 ;1] , sin[arcsin(x)] = x et cos[arccos(x)] = x y [- 2 2 ] , arcsin[sin(y)] = y et y [0 ;] , arccos[cos(y)] = y et x , tan[arctan(x)] = x y ]- 2 2 [ , arctan[tan(y)] = y .2) On a aussi : x[-1 ;1] , arcsin(-x) = -arcsin(x) et x
, arctan(-x) = -arctan(x) ; les fonctions arcsin et arctan sont donc impaires.( car sin et tan sont impaires) preuve : y = arcsin(-x) -x = sin(y) x = -sin(y) x = sin(-y) -y = arcsin(x) y = -arcsin(x) y = cos(x) y = arctan(x) y = tan(x) y = arccos(x) 33 Dérivées
On a démontré le théorème de dérivation d'une fonction réciproque d'une application bijective :
Si f est une fonction bijective et continue sur un intervalle ouvert contenant y 0 et si f est dérivable en y 0 et si f '(y 0 ) 0 , alors la bijection réciproque f -1 est dérivable en x 0 = f(y 0 ) et on a (f -1 )'(x 0 )('f1 0 y.En posant y = f
-1 (x) = arcsin(x) et x = f(y) = sin(y) on obtient : (f -1 )'(x) = [arcsin(x)]' = x- 1 1 * (x))cos(arcsin1 cosy1 (siny)'1 )y('f1 2 , x ]-1 ;1[ .(* cf. exercice 3a)Exercices : démontrer que : [arccos(x)]' =
x- 1 1- 2 x ]-1 ;1[ et [arctan(x)]' = 2 x 1 1 , x . remarque : la fonction arcsin n'est pas dérivable en x = -1 et en x = 1 ; calculons f d (1) et f ' g (-1) : f d (1) =01 x- 1 1 lim
21xet f g (-1) =
01 x- 1 1 lim
21xinterprétation géométrique : les tangentes au graphique de la fonction arcsin en 1 x et en 1 x sont verticales : 4
4 Exercices
1) Démontrer : x [-1 ;1] , arcsin(x) + arccos(x) =
22) Calculer le domaine de définition des fonctions f
i définies par : a) y = f 1 (x) = arcsin3 x21 x
b) y = f 2 (x) =1xarctanx
2 c) y = f 3 (x) = arccos 2 x1x23) Démontrer :
a) x [-1 ;1] , cos[arcsin(x)] = x 1 2 et sin[arccos(x)] = x 1 2 b) x ]-1 ;1[ , tan[arcsin(x)] = x- 1 x 2 c) x [-1 ;1]-{0} , tan(arccos(x)] = x x- 1 2 d) x , sin[arctan(x)] = x 1 x 2 et cos[arctan(x)] = x 1 1 24) Calculer les dérivées des fonctions f
i définies par : a) y = f 1 (x) = arcsin (2x-3) b) y = f 2 (x) = arccos(x 2 c) y = f 3 (x) = arctan (3x 2 ) d) y = f 4 (x) = arctan x1x15) Calculer :
a) dx x11 2 b) dx xa1 22( poser t = ax ) c) dx x 1 1 2 d) dx x 1 x 22
( poser t = arccos(x) x = cos(t) ) e) dx x 1 x 2 ( poser t = arctan(x) x = tan(t) ) f) dx arcsin(x) g) dx arccos(x) h) dx arccos(2x) i) dx arctan(x) x j) dx x- 1 2 k) dx x16 25 1 2
6) a) Calculer l'aire de la surface comprise entre le graphique de la fonctio définie par y = f(x) = arcsin(x),
l'axe des abscisses et les verticales x = 0 et x = 1 . b) Même question pour la fonction g définie par y = g(x) = arccos(x) .quotesdbs_dbs16.pdfusesText_22[PDF] trouver la fonction réciproque d'un polynome
[PDF] fonction réciproque exercices corrigés
[PDF] séquence pierre et le loup cycle 3
[PDF] fonction réciproque définition
[PDF] réciproque d'une fonction racine carré
[PDF] pierre et le loup cm2
[PDF] calcul fonction reciproque en ligne
[PDF] fonction réciproque dérivée
[PDF] activité réciproque du théorème de pythagore
[PDF] musique de film youtube
[PDF] pythagore 3eme exercices
[PDF] activité 2nd degré
[PDF] recherche musique de film
[PDF] musique de film compositeur
