 Tableaux des dérivées
Tableaux des dérivées
%20primitives
 Tableaux des dérivées et primitives et quelques formules en prime
Tableaux des dérivées et primitives et quelques formules en prime
%20d%C3%A9riv%C3%A9es
 Fiche : Dérivées et primitives des fonctions usuelles - Formulaire
Fiche : Dérivées et primitives des fonctions usuelles - Formulaire
Dans chaque ligne f′ est la dérivée de la fonction f sur l'intervalle I. f usur I est ln
 Tableau des dérivées élémentaires et règles de dérivation
Tableau des dérivées élémentaires et règles de dérivation
(u v. ) = u v − uv v2. Dérivée de la puissance. (un) = nu un−1. Dérivée de la racine. (√ u) = u. 2. √ u. Dérivée du logarithme. [ln(u)] = u u. Dérivée de l'
 DÉRIVÉES USUELLES ET DIFFÉRENTIELLES
DÉRIVÉES USUELLES ET DIFFÉRENTIELLES
Dérivée 1. Dérivée 2. Différentielle y = u(x) y' = u'(x) dy dx. = du dx dy = du y = Ln(u(x)) y' = u' u dy dx. = u' u dy = du u y = tan(x) y' =1 + tan2(x) = 1.
 Tableaux des dérivées Dérivées des fonctions usuelles Notes
Tableaux des dérivées Dérivées des fonctions usuelles Notes
f = ln u f ' = u' u u dérivable sur un intervalle I et u > 0 f (x) = u(ax + (1) La dérivée d'une fonction composée .... Toutes les lignes qui suivent ...
 formulaire.pdf
formulaire.pdf
Dérivées. Fonctions usuelles Fonctions usuelles. R`egles de dérivation. Exemples f(x) f′(x) f(x) f′(x) k. 0 x. 1. (u + v)′ = u′ + v′. (u × v)′ = u′v + uv′.
 T ES Fonction exponentielle
T ES Fonction exponentielle
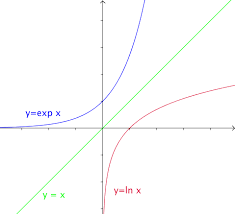
Dem : ln ( exp (x) ) = x les dérivées de ces deux fonctions sont donc toutes les deux égales à 1. [ln ( exp (x) )]' = )x exp(. ))'x. (exp(. )
 FONCTION LOGARITHME NEPERIEN
FONCTION LOGARITHME NEPERIEN
lnx x −1. = 0. V. Fonctions de la forme ln u. Propriété : Soit u une fonction Sa dérivée est la fonction x ! u'(x) u(x) . - Admis -. Exemple : Vidéo https ...
 Fiche : Dérivées et primitives des fonctions usuelles - Formulaire
Fiche : Dérivées et primitives des fonctions usuelles - Formulaire
Dans chaque ligne f? est la dérivée de la fonction f sur l'intervalle I. (ln
 )? = u? u. En particulier
)? = u? u. En particulier
. (ua)? = ?u?ua?1.
 formulaire.pdf
formulaire.pdf
x?+? ln(x)/xn = 0. Dérivées. Fonctions usuelles Fonctions usuelles. R`egles de dérivation. Exemples f(x) f?(x) f(x) f?(x) k. 0 x. 1. (u + v)? = u? + v?.
 Tableau des dérivées élémentaires et règles de dérivation
Tableau des dérivées élémentaires et règles de dérivation
1 Dérivation des fonctions élémentaires. Fonction. Df. Dérivée u. Dérivée du logarithme. [ln(u)] = u u. Dérivée de l'exponentielle. (eu) = u eu.
 Chapitre 15 Fonctions ln(u) et exp(u)
Chapitre 15 Fonctions ln(u) et exp(u)
15.2 Fonction exp(u). BTS Comptabilité Gestion. Remarque. Ce cas est généralisable : La dérivée de ln(u) est toujours du signe de u?(x) car comme.
 Tableaux des dérivées
Tableaux des dérivées
%20primitives
 Tableaux des dérivées et primitives et quelques formules en prime
Tableaux des dérivées et primitives et quelques formules en prime
%20d%C3%A9riv%C3%A9es
 DÉRIVÉES USUELLES ET DIFFÉRENTIELLES
DÉRIVÉES USUELLES ET DIFFÉRENTIELLES
DÉRIVÉES USUELLES ET DIFFÉRENTIELLES. DÉRIVÉES FONDAMENTALES. Fonction. Dérivée 1. Dérivée 2. Différentielle y = u(x) y' = u'(x) y = Ln(u(x)) y' = u' u.
 FONCTION LOGARITHME NEPERIEN
FONCTION LOGARITHME NEPERIEN
La fonction logarithme népérien notée ln
 Fonction logarithme népérien
Fonction logarithme népérien
Ainsi dans le cas d'une fonction de la forme f = ln(u)
 Fonction logarithme népérien
Fonction logarithme népérien
La fonction ln a pour dérivée a pour primitive ln x sur l'intervalle ]0 ; +?[. ... la fonction lnou qui à x associe ln(u(x)) est dérivable sur I.
Chapitre 15Fonctionsln(u)etexp(u)
Sommaire
15.1 Fonctionln(u). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 191
15.1.1 Définition. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 191
15.1.2 Dérivée. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 191
15.1.3 Résolutions d"équations et d"inéquations. . . . . . . . . . . . . . . . . . . . . . . 192
15.2 Fonctionexp(u). . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 192
15.2.1 Définition. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 192
15.2.2 Dérivée. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 192
15.2.3 Résolutions d"équations et d"inéquations. . . . . . . . . . . . . . . . . . . . . . . 193
15.3 Exercices. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 193
15.4 Travaux dirigés. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 197
15.1 Fonctionln(u)
15.1.1 Définition
Définition15.1.Soituunefonctionstrictementpositivesur unintervalleI.La fonctionf=ln(u) est la fonction définie surIparf:x?-→ln[u(x)].Exemple.Soitfla fonction définie parf:x?-→ln(x-4). Déterminer sur quel ensemble est définie
f.15.1.2 Dérivée
Propriété 15.1.Soit u une fonction strictement positive et de dérivée u?sur un intervalle I.
La fonction f:x?-→ln(u)est dérivable sur I et f?=u? u.Exemple.fest définie parf:x?-→ln(x2+4).
1. Vérifier quefest bien définie surR.
2. Calculerf?(x) et étudier son signe. En déduire les variationsdefsurR.
3. Comparer les variationsdefà celles dex?-→x2+4.
19115.2 Fonctionexp(u)BTS Comptabilité Gestion
Remarque.Ce cas est généralisable : La dérivée de ln(u) est toujours du signe deu?(x) car, comme
variations surI.15.1.3 Résolutions d"équations et d"inéquations
Équations de la formeln(u)=k
• On cherche d"abord sur quel intervalleJla fonctionuest strictement positive. Les solutions retenues après résolutiondevront être dansIet dansJ. • Onse ramènesurIàuneéquationdelaformeln[u(x)]=ln(a) aveca>0équivalenteàu(x)= aou bien on utilise la fonction exponentielle. • On ne retient parmi les solutionstrouvées que celles qui appartiennentàIet àJ. Exemple.Résoudre sur l"intervalleIdonné, les équations suivantes :1. ln(x+2)=0 surI=[0; 10]. 2. ln(x+2)=ln(3-x) surI=[0; 2].
Inéquations de la formeln(u)>k
• On cherche d"abord sur quel intervalleJla fonctionuest strictement positive. Les solutions retenues après résolutiondevront être dansIet dansJ. • Onse ramènesurIàuneéquationdelaformeln[u(x)]>ln(a) aveca>0équivalenteàu(x)= aou bien on utilise la fonction exponentielle. • On ne retient parmi les solutionstrouvées que celles qui appartiennentàIet àJ. Remarque.On procéde de même pour les autres types d"inéquations. Exemple.Résoudre sur [4; 10] l"inéquation ln(2x-6)<1.15.2 Fonctionexp(u)
15.2.1 Définition
Définition 15.2.Soituune fonction définie sur un intervalleI. La fonctionf=exp(u)=euest la fonction définie surIparf:x?-→exp[u(x)]=eu(x). Exemple.Soitfla fonction définie surRparf:x?-→e2x+1.15.2.2 Dérivée
Propriété 15.2.Soit u une fonction de dérivée u?sur un intervalle I. La fonction f:x?-→exp(u)=
e uest dérivable sur I et f?=u?×exp(u)=u?×eu.Exemple.fest définie parf:x?-→exp(-x2+3).
1. Calculerf?(x) et étudier son signe. En déduire les variationsdefsurR.
2. Comparer les variationsdefà celles dex?-→-x2+3.
Remarque.Ce cas est généralisable: La dérivée de exp(u) est toujoursdu signedeu?(x) car, comme
e u(x)>0, alorsf?(x) est du signe queu?(x). Ainsi exp(u) etuont les mêmes variationssurI. 192http://perpendiculaires.free.fr/
BTS Comptabilité Gestion15.3 Exercices
15.2.3 Résolutions d"équations et d"inéquations
Équations de la forme e
u=k • On vérifie d"abord quek>0, sinon l"équation n"a pas de solution.• On se ramène surIà une équation de la forme eu(x)=eaéquivalente àu(x)=aou bien on
utilise la fonction logarithmenépérien. Exemple.Résoudre surRles équations suivantes : 1. e x+2=3.2. ex2-1=1.Inéquations de la forme e
u>k • On examine le signe deket on en tire les conséquences.• On se ramène surIà une équation de la forme eu(x)>eaéquivalente àu(x)>aou bien on
utilise la fonction logarithmenépérien. Remarque.On procéde de même pour les autres types d"inéquations.Exemple.Résoudre surRles inéquations :
1. e -2x+1<3 2. ex+3>-1 3. ex2-1<-215.3 Exercices
EXERCICE15.1.1. Rappeler quel est le signe de ln(x) selon les valeurs dex.2. Déterminer le signe des fonctions suivantes sur l"intervalleIdonné :
(a)f(x)=ln(x)+1 surI=]0;+∞[. (b)f(x)=ln(x+8) sur ]-8;+∞[. EXERCICE15.2.1. Rappeler que est le signe de exselon les valeurs dex.2. Déterminer le signe des fonctions suivantes surR:
(a)f(x)=ex-1. (b)f(x)=e-x2-1. (c)f(x)=-0,5x+3 e0,5x.EXERCICE15.3.
Calculer la dérivée des fonctions suivantes sur l"intervalleIdonné :1.f(x)=ln(2x-4) surI=]2;+∞[.
2.f(x)=4x2+ln(1+x2) surI=R.
3.f(x)=1-ln(12-x) surI=[1; 6].4.f(x)=xln(2x+1) surI=]0;+∞[.
5.f(x)=[ln(x)]2surI=]0;+∞[.
6.f(x)=4
ln(2x-2)surI=]1;+∞[.EXERCICE15.4.
Pour chacune des fonctions suivantes définie sur l"intervalleI: • Calculerf?(x); • Étudier le signe def?(x); • Dresser le tableau des variations def.1.fdéfiniesurI=[1; 30]parf:x?-→x+50-18ln(x).
2.fdéfinie surI=[-2; 2] parf:x?-→
ln(x2+5).David ROBERT193
15.3 ExercicesBTS Comptabilité Gestion
EXERCICE15.5.
Une entreprisefabriqueet vendqtonnesd"unproduitde base. Lebénéfice réalisé,enmilliersd"eu-
ros, pour produire cesqtonnes est défini sur l"intervalle [0,5; 9] par :B(q)=0,5q2-14q-68+49ln(2q+4)
1. L"entreprise réalise-t-ell un profit lorsqu"elle vend 2 tonne de produit? 5 tonnes? 8 tonnes?
2. (a) Déterminer l"expression du bénéfice marginalB?(q), dérivé du bénéfice.
(b) À la calculatrice, calculer le bénéfice marginal pour 2,13 tonnes. (c) Pour une tonne, le bénéfice marginal est-il positif? Mêmequestion pour 4 tonnes.3. (a) Utiliserla calculatricepour trouver la quantitéà partir de laquelle l"entrepriseréalise un
bénéfice marginal négatif sur [0,5; 9].(b) D"après le tableau de valeurs du bénéfice marginalB?(q), commenter les valeurs du bé-
néfice marginal de part et d"autre de 5 tonnes.EXERCICE15.6.
Calculer la dérivée des fonctions suivantes :1.f(x)=e2x.
2.f(x)=e-4x2.3.f(x)=4ex-e2x.
4.f(x)=10xe-x.5.f(x)=(x-1)e0,5x.
6.f(x)=2
1+e2x-3.
EXERCICE15.7.
Le bénéfice engendré par la vente de peluches est modélisé parB(q)=12-q-e4-qoùqest en
milliers de peluches,q?[1,5; 14] etB(q) est en milliers d"euros.1. Calculer la dérivée de la fonctionBet étudier le signe deB?(q).
En déduire le sens de variation de la fonctionBsur [1,5; 14].2. Quelle quantité de peluches à vendre permet de réaliser unbénéfice maximal?
3. Justifier le nombre de solutionsde l"équationB(q)=0 dans l"intervalle [1,5; 14].
En utilisant la calculatrice, donner une valeur arrondie deces solutions à 0,001 près.4. En déduire la plage de profit. Arrondir à une peluche près.
EXERCICE15.8.
Sur le marché en gros à Nantes, l"offre de champignonspleurotes, en tonnes, peut se modéliser par
la fonctionfet la demande par la fonctiongtelles que :f(x)=1,5ln(x-2)+4 etg(x)=2e-x+3+2, pour un prixxentre 2,5 et 5?par kg.1. Visualiser à la calculatrice, dans une fenêtre adaptée, les courbes des fonctionsfetget dé-
terminer le prix d"équilibre du marché.2. Calculer les dérivées de ces deux fonctionsfetget étudier le signe def?(x) etg?(x).
En déduire le sens de variation des fonctionsfetgsur [2,5; 5].3. Résoudre les équationsf(x)=4 etg(x)=4.
4. Sur ce marché, à quel prix l"offre est-elle égale à la demande?
Quelle est la quantitéde pleurotes échangées au prix d"équilibre? 194http://perpendiculaires.free.fr/
BTS Comptabilité Gestion15.3 Exercices
EXERCICE15.9.
Une entreprisede loisirsquipossède 60 bateauxles loueà lasemaine. Les donnéesfinancièressont
exprimées en milliersd"euros (k?) et les résultats demandés seront arrondis à 10-2près.
Partie A :Étude du coût de fonctionnement hebdomadaire Le coût de fonctionnement hebdomadaireC(q), exprimé en milliers d"euros, correspondant à la location d"un nombreqde bateaux est donné par :C(q)=15+2q-20ln(0,1q+1) pour0?q?60.
1. (a) CalculerC(10) etC(20). Le coût de fonctionnement hebdomadaire est-il propor-
tionnel au nombre de bateaux loués? (b) Déterminer le pourcentage d"augmentation du coût de fonctionnement hebdoma- daire lorsque le nombre de bateaux loués passe de 10 à 20.2. (a) Montrer queC?(q)=0,2q
0,1q+1.
En déduire le sens de variation de la fonctionCsur l"intervalle [0; 60]. (b) Calculer le coût de fonctionnement hebdomadairemaximal (exprimé en k?).Partie B :Étude du bénéfice
Chaque bateau est loué 3000 euros la semaine.
1. Montrer que le bilan financier hebdomadaireB(q), exprimé en k?, correspondant à la
location d"un nombreqde bateaux est donné par :B(q)=q+20ln(0,1q+1)-15 pour0?q?60.
2. CalculerB?(q) et en déduire le sens de variation de la fonctionBsur l"intervalle [0; 60].
3. (a) Compléter le tableau de valeurs suivant :
q051020304060
B(q)-1527
(b) ConstruirelareprésentationgraphiqueCdelafonctionBdanslerepèredelafigure15.1page suivante.
4. Déterminer graphiquement, en faisant figurer les tracés utiles, le nombre minimum de
bateaux que l"entreprise doit louer pendant cette semaine pour obtenir : (a) Un bénéfice (positif); (b) Un bénéfice supérieur à 20k?.EXERCICE15.10.
est modélisée parf(q)=5+10e-0,3qet la fonction demande parg(q)=495+10e-0,3q, les prixf(q) et
g(q) sont exprimés en euro par kg.1. (a) Calculer la dérivée des fonctionsfetget étudier le signe def?(q) etg?(q).
(b) En déduire le sens de variation des fonctionsfetgsur [2; 7].2. (a) Représenter ces deux fonctions à l"écran de la calculatrice dans la fenêtre :X?[2; 7] et
Y?[0; 11].
Existe-t-ilunpoint d"intersectionentreles deux courbes? Endéterminerl"abscisseqEet l"ordonnéepE. (b) Retrouver le résultat par le calcul en résolvant l"équationf(q)=g(q) sur l"intervalle [2; 7]. (c) Interpréter les nombrespEetqE.David ROBERT195
15.3 ExercicesBTS Comptabilité Gestion
FIGURE15.1: Repère de l"exercice
15.910 20 30 40 50 60
-10 -201020304050607080
O xy3. Les consommateurssont très demandeurs, et veulent 7 tonnes de produit.
Quel est le prix correspondant à cette demande? Y a-t-il excédent ou pénurie de ce produit sur le marché? Justifier.4. Pour faire face à leur frais et aux nouveaux impôts, les producteurs offrent leur produit à un
prix de 8 euro le kg.Y a-t-il excédent ou pénurie de ce produit sur le marché? Pourcela, estimer l"offre et la de-
mande à ce prix. 196http://perpendiculaires.free.fr/ BTS Comptabilité Gestion15.4 Travaux dirigés
15.4 Travaux dirigés
EXERCICE15.11(Fonction logistique).
Partie A :Ajustements
Depuis l"année 2003, on étudie le taux d"équipement des 12 ans et plus en ordinateurs et internet à domicile. Les résultatssont donnés dans le tableau suivant :Année
2003200420052006200720082009201020112012
Rangxi0123456789
Taux d"équipementyi15,419,42429,335,241,447,854,260,265,81. Ajustement affine
(a) Représenter le nuage de points associés à la série (xi;yi) dans la figure15.2page
suivante.FIGURE15.2: Repère de l"exercice
15.111 2 3 4 5 6 7 8 9 10 11 12 13 14-1
-10102030405060708090100
O xy (b) Unajustementaffinevoussemble-t-iljustifié?Vérifierendéterminantlecoefficient de corrélation avec la calculatrice. (c) Déterminer, à l"aide de la calculatrice, l"équation de la droiteDd"ajustement dey enxobtenue par la méthode des moindres carrés. Arrondir les coefficients au cen- tième. Tracer la droiteDsur le graphique précédent. (d) À l"aide de cet ajustement,quel taux peut-on prévoir pour 2017?David ROBERT197
15.4 Travaux dirigésBTS Comptabilité Gestion
(e) Cet ajustement reste-t-il valable sur le moyen terme?2. Ajustement logistique
Compte-tenudes limitesde notre ajustementaffine, on envisage unajustement du taux d"équipement par une fonction logistiquefdéfinie sur [0; 30] par :f(x)=c1+ae-bxavec
a,betcdes nombres réels. (a) Donner,avec lacalculatrice,lavaleur debarrondiel"unitéet celledeaetcarrondieà 10
-2près. Pour les Casio :calc,REG, puis faire défiler avec F6 etLgst.Pour les TI :CALC, puis8 :Logistic.
(b) À l"aide de cet ajustement,quel taux peut-on prévoir pour 2017?Partie B :Étude de l"ajustement
Dans la suite,onadmet que lapartdes 12 anset plusayant internetàla maisonest modélisée par la fonctionfdéfinie sur [0; 30] parf(x)=921+e1,6-0,28xoùxest le temps écoulé depuis 2000,
exprimé en années, etf(x) le taux d"équipement en %.1. Calculerf(10) et interpréter le résultat.
2. On a obtenu ci-contre, la dérivée de la fonctionfà l"aide d"un logiciel de calcul formel :
(a) Donner, sans justification, l"expression def?(x). (b) Justifier que la dérivée est positive sur [0; 30]. En déduire le tableau de variation de la fonctionfsur [0; 30]. (c) Justifier que l"équationf(x)=90 a une unique solutionx0dans l"intervalle [0; 30]. (d) Donner un encadrement d"amplitude0,1 dex0.3. Peut-on prévoir que 92% des 12 ans et plus seront équipés d"internet à domicile?
198http://perpendiculaires.free.fr/quotesdbs_dbs6.pdfusesText_12
[PDF] dérivée usuelle
[PDF] dérivées
[PDF] dernier bordereau cnss visa
[PDF] dernier delai
[PDF] dernier delai campus france maroc
[PDF] dernier delai campus france maroc 2017
[PDF] dernier delai declaration impots
[PDF] dernier jour d'un condamné chapitre 13 figure de style
[PDF] dernier journal france 24 du 25 juin 2009
[PDF] dernieres news tunisie
[PDF] deroulement echo doppler des arteres renales
[PDF] derramamiento del espiritu santo en pentecostes
[PDF] des c hoses dangereux qui peuvent vous tuer
[PDF] des cellules photovoltaïques pour un tour du monde en avion correction

