Tableaux des dérivées
%20primitives
Tableaux des dérivées et primitives et quelques formules en prime
%20d%C3%A9riv%C3%A9es
Fiche : Dérivées et primitives des fonctions usuelles - Formulaire
Dans chaque ligne f′ est la dérivée de la fonction f sur l'intervalle I. f usur I est ln
Tableau des dérivées élémentaires et règles de dérivation
(u v. ) = u v − uv v2. Dérivée de la puissance. (un) = nu un−1. Dérivée de la racine. (√ u) = u. 2. √ u. Dérivée du logarithme. [ln(u)] = u u. Dérivée de l'
Chapitre 15 Fonctions ln(u) et exp(u)
Soit u une fonction strictement positive et de dérivée u′ sur un intervalle I . La fonction f : x − → ln(u) est dérivable sur I et f ′ = u′ u . Exemple. f
DÉRIVÉES USUELLES ET DIFFÉRENTIELLES
Dérivée 1. Dérivée 2. Différentielle y = u(x) y' = u'(x) dy dx. = du dx dy = du y = Ln(u(x)) y' = u' u dy dx. = u' u dy = du u y = tan(x) y' =1 + tan2(x) = 1.
Tableaux des dérivées Dérivées des fonctions usuelles Notes
f = ln u f ' = u' u u dérivable sur un intervalle I et u > 0 f (x) = u(ax + (1) La dérivée d'une fonction composée .... Toutes les lignes qui suivent ...
formulaire.pdf
Dérivées. Fonctions usuelles Fonctions usuelles. R`egles de dérivation. Exemples f(x) f′(x) f(x) f′(x) k. 0 x. 1. (u + v)′ = u′ + v′. (u × v)′ = u′v + uv′.
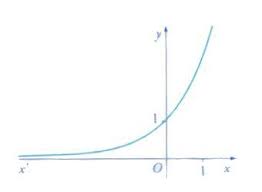T ES Fonction exponentielle
Dem : ln ( exp (x) ) = x les dérivées de ces deux fonctions sont donc toutes les deux égales à 1. [ln ( exp (x) )]' = )x exp(. ))'x. (exp(. )
FONCTION LOGARITHME NEPERIEN
lnx x −1. = 0. V. Fonctions de la forme ln u. Propriété : Soit u une fonction Sa dérivée est la fonction x ! u'(x) u(x) . - Admis -. Exemple : Vidéo https ...
Fiche : Dérivées et primitives des fonctions usuelles - Formulaire
Dans chaque ligne f? est la dérivée de la fonction f sur l'intervalle I. (ln
)? = u? u. En particulier
. (ua)? = ?u?ua?1.
formulaire.pdf
x?+? ln(x)/xn = 0. Dérivées. Fonctions usuelles Fonctions usuelles. R`egles de dérivation. Exemples f(x) f?(x) f(x) f?(x) k. 0 x. 1. (u + v)? = u? + v?.
Tableau des dérivées élémentaires et règles de dérivation
1 Dérivation des fonctions élémentaires. Fonction. Df. Dérivée u. Dérivée du logarithme. [ln(u)] = u u. Dérivée de l'exponentielle. (eu) = u eu.
Chapitre 15 Fonctions ln(u) et exp(u)
15.2 Fonction exp(u). BTS Comptabilité Gestion. Remarque. Ce cas est généralisable : La dérivée de ln(u) est toujours du signe de u?(x) car comme.
Tableaux des dérivées
%20primitives
Tableaux des dérivées et primitives et quelques formules en prime
%20d%C3%A9riv%C3%A9es
DÉRIVÉES USUELLES ET DIFFÉRENTIELLES
DÉRIVÉES USUELLES ET DIFFÉRENTIELLES. DÉRIVÉES FONDAMENTALES. Fonction. Dérivée 1. Dérivée 2. Différentielle y = u(x) y' = u'(x) y = Ln(u(x)) y' = u' u.
FONCTION LOGARITHME NEPERIEN
La fonction logarithme népérien notée ln
Fonction logarithme népérien
Ainsi dans le cas d'une fonction de la forme f = ln(u)
Fonction logarithme népérien
La fonction ln a pour dérivée a pour primitive ln x sur l'intervalle ]0 ; +?[. ... la fonction lnou qui à x associe ln(u(x)) est dérivable sur I.
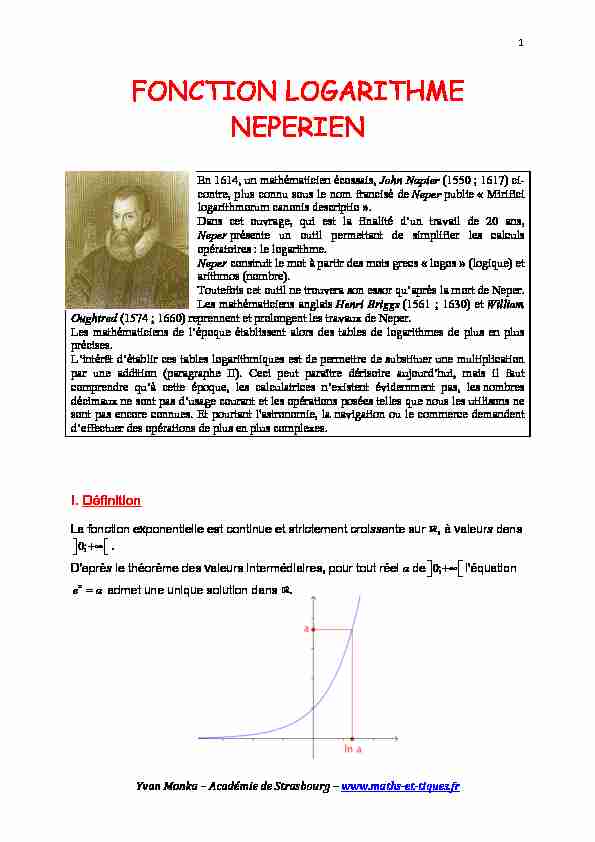
1YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.frFONCTION LOGARITHME NEPERIEN En 1614, un mathématicien écossais, John Napier (1550 ; 1617) ci-contre, plus connu sous le nom francisé de Neper publie " Mirifici logarithmorum canonis descriptio ». Dans cet ouvrage, qui est la fina lité d'un trava il de 20 ans , Neper présente un outil permetta nt de simplifier le s calculs opératoires : le logarithme. Neper construit le mot à partir des mots grecs " logos » (logique) et arithmos (nombre). Toutefois cet outil ne trouvera son essor qu'après la mort de Neper. Les mathématiciens anglais Henri Briggs (1561 ; 1630) et William Oughtred (1574 ; 1660) reprennent et prolongent les travaux de Neper. Les mathématiciens de l'époque établissent alors des tables de logarithmes de plus en plus précises. L'intérêt d'établir ces tables logarithmiques est de permettre de substituer une multiplication par une addi tion (paragra phe II). Ceci peut paraît re dérisoire aujourd'hui, ma is il faut comprendre qu'à cette é poque, les calculatrices n'existent évidemment pas, les nombres décimaux ne sont pas d'usage courant et les opérations posées telles que nous les utilisons ne sont pas encore connues. Et pourtant l'astronomie, la navigation ou le commerce demandent d'effectuer des opérations de plus en plus complexes. I. Définition La fonction exponentielle est continue et strictement croissante sur ℝ, à valeurs dans
0;+∞
. D'après le théorème des valeurs intermédiaires, pour tout réel a de0;+∞
l'équation e x =a admet une unique solution dans ℝ.2YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.frDéfinition : On appelle logarithme népérien d'un réel strictement positif a, l'unique solution de l'équation
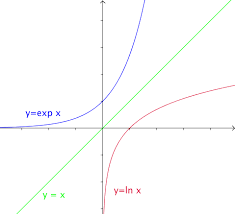
e x =a . On la note lna . La fonction logarithme népérien, notée ln, est la fonction : ][ ln:0;+∞→ x!lnxRemarques : - Les fonctions exp et ln sont des fonctions réciproques l'une de l'autre. - Les courbes représentatives des fonctions exp et ln sont symétriques par rapport à la droite d'équation
y=x. - Dans le domaine scientifique, on utilise la fonction logarithme décimale, notée log est définie par :
log(x)= lnx ln10Conséquences : a)
y=lnxavecx>0⇔x=e y b) ln1=0 lne=1 ln 1 e =-1 c) Pour tout x, lne x =x d) Pour tout x strictement positif, e lnx =xDémonstrations : a) Par définition b) - Car
e 0 =1 - Car e 1 =e - Car e -1 1 e c) Si on pose y=e x , alors x=lny=lne x d) Si on pose y=lnx , alors x=e y =e lnxII. Propriété de la fonction logarithme népérien 1) Relation fonctionnelle Théorème : Pour tous réels x et y strictement positifs, on a : ()lnlnln xyxy ×=+
3YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.frDémonstration :
e ln(x×y) =x×y=e lnx ×e lny =e lnx+lnyDonc ()lnlnln xyxy ×=+
Remarque : Cette formule permet de transformer un produit en somme. Ainsi, celui qui aurait à effectuer 36 x 62, appliquerait cette formule, soit : log(36 x 62) = log(36) + log(62) ≈ 1,5563 + 1,7924 (voir table ci-contre) L'addition étant beaucoup plus simple à effectuer que la multiplication, on trouve facilement : log(36 x 62) ≈ 3,3487 En cherchant dans la table, le logarithme égal à 3,3487, on trouve 2232, soit : 36 x 62 = 2232. 2) Conséquences Corollaires : Pour tous réels x et y strictement positifs, on a : a)
ln 1 x =-lnx b) ln x y =lnx-lny c) lnx= 1 2 lnx d) lnx n =nlnx avec n entier relatif Démonstrations : a) 11 lnlnln ln1 0xx xx b) 11 lnlnln lnlnln x xxxy yyy c) ()2lnlnl nlnlnxxxxxx=+=×=
d) On démontre ce résultat par récurrence. L'initialisation est triviale. La démonstration de l'hérédité passe par la décomposition : ()
1 lnlnln lnln ln(1 )ln nnn xxxxxnxxnx4YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.frMéthode : Simplifier une expression Vidéo https://youtu.be/HGrK77-SCl4 ()()
ln35 ln3 5A=-++B=3ln2+ln5-2ln3
C=lne 2 -ln 2 e ln35 ln3 5 ln35 35 ln95 ln4 A=-++B=3ln2+ln5-2ln3
=ln2 3 +ln5-ln3 2 =ln 2 3 ×5 3 2 =ln 409 C=lne 2 -ln 2 e =2lne-ln2+lne =2-ln2+1 =3-ln2
III. Etude de la fonction logarithme népérien 1) Continuité et dérivabilité Propriété : La fonction logarithme népérien est continue sur
0;+∞
. - Admis - Propriété : La fonction logarithme népérien est dérivable sur0;+∞
et (lnx)'= 1 x . Démonstration : La fonction ln est continue sur0;+∞
, donc pour tout réel a > 0, on a : lim x→a lnx=lna . Donc par composée de limites, en posant X=lnx lim x→a lnx-lna x-a =limX→lna
X-lna e Xquotesdbs_dbs2.pdfusesText_2[PDF] dérivée usuelle
[PDF] dérivées
[PDF] dernier bordereau cnss visa
[PDF] dernier delai
[PDF] dernier delai campus france maroc
[PDF] dernier delai campus france maroc 2017
[PDF] dernier delai declaration impots
[PDF] dernier jour d'un condamné chapitre 13 figure de style
[PDF] dernier journal france 24 du 25 juin 2009
[PDF] dernieres news tunisie
[PDF] deroulement echo doppler des arteres renales
[PDF] derramamiento del espiritu santo en pentecostes
[PDF] des c hoses dangereux qui peuvent vous tuer
[PDF] des cellules photovoltaïques pour un tour du monde en avion correction
