 I Asymptote Oblique II Branches paraboliques
I Asymptote Oblique II Branches paraboliques
II Branches paraboliques. II.1 Branche parabolique de direction (Ox). On dit que Cf présente une branche parabolique de direction asymptotique (Ox) en +∞ si :.
 Chapitre 11. (Complément) sur le comportement asymptotique des
Chapitre 11. (Complément) sur le comportement asymptotique des
est 0 on dit que la courbe possède une branche parabolique de direction l'axe des abscisses (Ox) (c'est le cas en particulier du logarithme). Enfin
 Branches infinies
Branches infinies
la branche infinie est une branche parabolique horizontale. Exemples : f x x. ( ) =
 Exemples à connaître de branches infinies
Exemples à connaître de branches infinies
On dit qu'il y a une direction asymptotique verticale. Il y a même une branche parabolique verticale (c'est-à-dire qu'il y a une direction mais l'écart
 Etude des branches infinies de la courbe représentative dune fonction
Etude des branches infinies de la courbe représentative dune fonction
12 déc. 2003 ... direction asymptotique en x0. ... – cette limite existe et appartient `a {+∞−∞}
 PERNOT MOISSON - Étude des points à linfini dune courbe
PERNOT MOISSON - Étude des points à linfini dune courbe
— DIRECTION ASYMPTOTIQUE SIMPLE. Soit y— CJ = O cette direction. L'équation forme de la branche parabolique à étudier. On peut écrire. <p»-i(tf
 COURBES PARAMETREES
COURBES PARAMETREES
1 nov. 2004 on dit que la courbe admet une branche parabolique de direction asymptotique la droite vectorielle d'équation y = Bx. Si lim t→t0y(t) − Bx ...
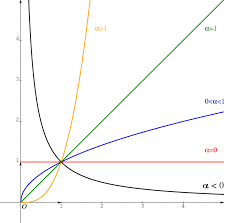 Étude de fonction et fonctions usuelles
Étude de fonction et fonctions usuelles
f(x) − ax = ±∞ : branche parabolique de direction asymptotique y = ax. Exemple 5. Déterminer les branches infinies de la fonction f définie par f(x) = 2
 Branches infinies dune fonction f
Branches infinies dune fonction f
petit par rapport à x.) c3) Branche parabolique de direction asymptotique ( ). Oy.. lim et lim. B.P. de direction ( ) x x. f x. f x. Oy x.
 I Asymptote Oblique II Branches paraboliques
I Asymptote Oblique II Branches paraboliques
II Branches paraboliques. II.1 Branche parabolique de direction (Ox). On dit que Cf présente une branche parabolique de direction asymptotique (Ox) en +?
 Vademecum sur létude des fonctions
Vademecum sur létude des fonctions
Limites et étude des branches asymptotiques aux bords du domaine de définition. branche parabolique de direction verticale.
 Chapitre 11. (Complément) sur le comportement asymptotique des
Chapitre 11. (Complément) sur le comportement asymptotique des
asymptotique des fonctions réelles possède une branche parabolique dont l'axe est donné par la direction que regarde la courbe. Plus précisément.
 Branches infinies
Branches infinies
On dit que f possède une branche infinie en a si lim ( ) est une branche parabolique horizontale. Exemples : f x.
 Etude de branches infinies. 1 Démarche
Etude de branches infinies. 1 Démarche
- Si c'est +? pas d'asymptote mais une branche parabolique d'axe oblique. 2. Page 3. 2 Exercices. Exercice 1 Étudier le comportement asymptotique des
 COURBES PARAMETREES
COURBES PARAMETREES
1 nov. 2004 on dit que la courbe admet une branche parabolique de direction asymptotique la droite vectorielle d'équation y = Bx.
 TECHNIQUES & MÉTHODES S03 ÉTUDE DE FONCTIONS
TECHNIQUES & MÉTHODES S03 ÉTUDE DE FONCTIONS
Exemple : La fonction ln x + ?2 x ? 1 présente une branche parabolique de direction asymptotique (Ox) en +?. 0. 1. 2. 3. 4. 5. 6. 7. 8.
 PERNOT MOISSON - Étude des points à linfini dune courbe
PERNOT MOISSON - Étude des points à linfini dune courbe
que le genre des branches paraboliques. I. — DIRECTION ASYMPTOTIQUE SIMPLE. Soit y— CJ = O cette direction. L'équation de la courbe est de la forme.
 Fiche méthode : Etude de fonctions
Fiche méthode : Etude de fonctions
notions : les asymptotes et les branches paraboliques. Asymptote verticale branche parabolique de direction asymptotique la droite d'équation.
 Etude des branches infinies de la courbe représentative dune fonction
Etude des branches infinies de la courbe représentative dune fonction
12 déc. 2003 direction asymptotique de Cf en x0 si limx?x0x?I. ?. ((OMx)
 [PDF] I Asymptote Oblique II Branches paraboliques - My MATHS SPACE
[PDF] I Asymptote Oblique II Branches paraboliques - My MATHS SPACE
On dit que Cf présente une branche parabolique de direction asymptotique (Ox) en +? si : asymptotique la droite d'équation y = ax en +? si :
 [PDF] Chapitre 11 (Complément) sur le comportement asymptotique des
[PDF] Chapitre 11 (Complément) sur le comportement asymptotique des
Enfin si ce même rapport tend vers l'infini on dit que la courbe possède une branche parabolique de direction l'axe des ordonnées (Oy) (ce qui est le cas de l
 [PDF] Branches infinies
[PDF] Branches infinies
La branche infinie est une asymptote horizontale d'équation y=l 2° cas : a?R l=+? La branche
 [PDF] Les branches infinies de la courbe ( )f
[PDF] Les branches infinies de la courbe ( )f
de direction : Oy ( )f C admet une branche parabolique de direction : y ax = ( ) ( )f ladroite D :y ax b est asymptote à C
 [PDF] Etude de branches infinies 1 Démarche
[PDF] Etude de branches infinies 1 Démarche
Soit lim x?+? f(x) ? ax = ±? et la courbe de f admet une branche parabolique de direction y = ax Exemples : f(x) = x +
 [PDF] Branches infinies dune fonction f
[PDF] Branches infinies dune fonction f
branche parabolique dont l'axe est donné par la direction que regarde la courbe c2) Branche parabolique de direction asymptotique ( )
 [PDF] Branches-infiniespdf - PTSI 1 Eucalyptus
[PDF] Branches-infiniespdf - PTSI 1 Eucalyptus
? ± ? le graphe de admet une branche parabolique de direction asymptotique la droite d'équation = ii Si ( ) ? ?±?
 [PDF] Vademecum sur létude des fonctions
[PDF] Vademecum sur létude des fonctions
Limites et étude des branches asymptotiques aux bords du domaine de définition branche parabolique de direction verticale
 Etude des branches infinies - Cas des courbes représentatives
Etude des branches infinies - Cas des courbes représentatives
On dit alors que Cf C f admet une branche parabolique ou encore que Cf C f admet une direction asymptotique On distingue 3 cas : a=±
 [PDF] techniques & méthodes s03 - MPSI Saint-Brieuc
[PDF] techniques & méthodes s03 - MPSI Saint-Brieuc
Branche parabolique de direction (Ox) Définition : On dit que Cf présente une branche parabolique de direction asymptotique (Ox) en +? si :
Comment déterminer la branche parabolique ?
Quand la courbe semble regarder dans une direction mais tout en s'en éloignant, on dit que la courbe poss? une branche parabolique dont l'axe est donné par la direction que regarde la courbe.Comment déterminer les branches infinies ?
Etude de branches infinies. Étant donnée une fonction f : R ?? R, l'étude de ses branches infinies a pour objectif de comprendre en détails le comportement de f(x) quand x tend vers +? ou ??. interprétation des différents résultats que l'on peut obtenir pour ce calcul.Comment montrer que Cf admet une branche parabolique ?
f(x) = l ? R, alors on dit que Cf admet une asymptote horizontale y = l au voisinage de +?. = ±?, alors on dit que Cf admet une branche parabolique de direction l'axe des ordonnées. = 0, alors on dit que Cf admet une branche parabolique de direction l'axe des abscisses.- Lorsqu'une limite à l'infini est infinie, il est possible qu'une asymptote oblique existe. Elle s'écrit sous la forme y=ax+b y = a x + b puisqu'elle est l'expression d'une droite.
Etude de branches innies.
1 Demarche
Etant donnee une fonctionf:R!R, l'etude de ses branches innies a pour objectif de comprendre en details le comportement def(x) quandxtend vers +1ou1. La premiere chose a faire est donc de calculer lim x!+1f(x). On peut alors donner une premiere interpretation des dierents resultats que l'on peut obtenir pour ce calcul. On distingue prin- cipalement deux types de resultats possibles. (Remarque : ici, on travaillera autour de +1, mais l'on pourrait faire exactement la m^eme chose autour de1). Premier cas.Cette limite est nie : limx!+1f(x) =`2R: On conclue alors que la courbe admet uneasymptote horizontaled'equationy=`en +1 et l'etude est terminee.Exemples :
f(x) =1x ; g(x) =xex; h(x) =2x2+ 1x 2+ 3 Second cas.Cette limite est innie : limx!+1f(x) = +1: La fonctionfn'admet alors pas d'asymptote horizontale en +1et l'on doit poursuivre l'etude pour etudier de plus pres le comportement def(x) autour de +1. Intuitivement, le calcul de limx!+1f(x) nous dit dans ce cas la quef(x) grandit quandxgrandit. Les questions qui se pose a ce moment la sont : \a quelle vitesse granditf(x)? Grandit-elle plus vite ou moins vite quex?" La encore, un calcul de limite va pouvoir nous aider a repondre : pour comparer la croissance def(x) et celle dex, on calcule limx!+1f(x)x Le comportement de la fonctionfautour de +1dependra alors du type de reponse obtenu mais contrairement a tout a l'heure, on distingue ici trois types de reponses possibles (et non plus deux).Soit lim
x!+1f(x)x = 0:Dans ce cas,f(x) grandit moins vite quex.Exemples :
f(x) = ln(x); g(x) =px; h(x) =x2+ 12 px3: 1 On dit que la courbe defadmet une branche parabolique d'axe (Ox).Soit lim
x!+1f(x)x = +1. Dans ce cas,f(x) grandit plus vite quex.Exemples :
f(x) =ex; g(x) =x2; h(x) =x4+ 2x31x 2+ 4: On dit que la courbe defadmet une branche parabolique d'axe (Oy).Soit lim
x!+1f(x)x =a2R. Dans ce cas, la vitesse de croissance def(x) est comparable a celle deaxquandxgrandit. Pour eectuer cette comparaison, on etudie une derniere limite : celle de la dierencef(x)axet on distingue deux cas :Soi tlim
x!+1f(x)ax=b2Ret la courbe defadmet la droite d'equationy=ax+b pour asymptote oblique.Exemples :
f(x) =x3+x+ 1x2+ 4; g(x) =x(px
2+ 2xpx
2+ 1); h(x) =x2lnx+ 2x
Soi tlim
x!+1f(x)ax=1et la courbe defadmet une branche parabolique de directiony=ax.Exemples :
f(x) =x+px; g(x) =x2lnx+ 1lnx ********************Resume :1. Calcul de lim
x!+1f(x).- Si c'est un reel`, asymptote d'equationy=`.- Si c'est +1, passer a l'etape 2.2. Si le resultat precedent est +1, calcul de limx!+1f(x)x
.- Si c'est 0 ou +1, pas d'asymptote mais une branche parabolique.- Si c'est un reelanon nul, passer a l'etape 3.3. Si le resultat precedent est un nombre non nula2R, calcul de limx!+1f(x)ax.- Si c'est un reelb, la droite d'equationy=ax+best alors asymptote a la courbe def.- Si c'est +1, pas d'asymptote mais une branche parabolique d'axe oblique.2
2 Exercices
Exercice 1
Etudier le comportement asymptotique des fonctions suivantes. g(x) =cos(x)x ; h(x) =p9x4+ 3x31x 2+ 1:Exercice 2
Etudier le comportement a l'inni des fonctions suivantes f:x7!2x3+x1x2+ 1; g(x) =px
9+ 2xx
21Exercice 3Soientfetgdenies par
f(x) = ln1 +xx ; g(x) =x+ 2ln1 +xx 1. Etudier le comportement defautour de +1. Donner l'equation de l'eventuelle asymp- tote. 2. A l'aide de la question precedente, etudier le comportement de la fonctiongen +1.3 Complements
En realite, l'etude des branches innies d'une fonctionfpourrait se resumer a la question suivante : \Existe-t-il une fonction plus simple quefqui se comporte commefautour de +1?" Pour repondre a cela, on cherche donc une fonctiongplus simple telle que lim x!+1f(x)g(x) = 0: Dans la premiere partie, on se contente de comparerfavec des fonctions anes (i.e. des droites). Mais rien ne nous empeche de comparerfa des fonctions plus complexes. Exercice 4Montrer que les courbes associees aux fonctionsf:x7!px4+ sin(x) etg:x7!x2
sont asymptotiques. Exercice 5Montrer que les courbes des fonctions suivantes sont asymptotiques. f(x) =ex+ex2 ; g(x) =exex2 3quotesdbs_dbs2.pdfusesText_2[PDF] etudes des fonctions branches infinies
[PDF] mode d'emploi lave linge brandt
[PDF] comment utiliser machine a laver brandt
[PDF] bras de levier définition
[PDF] levier inter appui
[PDF] cours moment d'une force par rapport ? un axe
[PDF] bras de levier calcul
[PDF] moment d'une force cours
[PDF] moment d'une force par rapport ? un axe pdf
[PDF] moment de force exercice
[PDF] moment d'un couple de force
[PDF] brassage interchromosomique et intrachromosomique animation
[PDF] brassage allélique définition
[PDF] definition brassage allelique
