 I Asymptote Oblique II Branches paraboliques
I Asymptote Oblique II Branches paraboliques
II Branches paraboliques. II.1 Branche parabolique de direction (Ox). On dit que Cf présente une branche parabolique de direction asymptotique (Ox) en +∞ si :.
 Chapitre 11. (Complément) sur le comportement asymptotique des
Chapitre 11. (Complément) sur le comportement asymptotique des
est 0 on dit que la courbe possède une branche parabolique de direction l'axe des abscisses (Ox) (c'est le cas en particulier du logarithme). Enfin
 Etude de branches infinies. 1 Démarche
Etude de branches infinies. 1 Démarche
- Si c'est +∞ pas d'asymptote mais une branche parabolique d'axe oblique. 2. Page 3. 2 Exercices. Exercice 1 Étudier le comportement asymptotique des
 Branches infinies
Branches infinies
la branche infinie est une branche parabolique horizontale. Exemples : f x x. ( ) =
 Exemples à connaître de branches infinies
Exemples à connaître de branches infinies
On dit qu'il y a une direction asymptotique verticale. Il y a même une branche parabolique verticale (c'est-à-dire qu'il y a une direction mais l'écart
 Etude des branches infinies de la courbe représentative dune fonction
Etude des branches infinies de la courbe représentative dune fonction
12 déc. 2003 ... direction asymptotique en x0. ... – cette limite existe et appartient `a {+∞−∞}
 PERNOT MOISSON - Étude des points à linfini dune courbe
PERNOT MOISSON - Étude des points à linfini dune courbe
— DIRECTION ASYMPTOTIQUE SIMPLE. Soit y— CJ = O cette direction. L'équation forme de la branche parabolique à étudier. On peut écrire. <p»-i(tf
 COURBES PARAMETREES
COURBES PARAMETREES
1 nov. 2004 on dit que la courbe admet une branche parabolique de direction asymptotique la droite vectorielle d'équation y = Bx. Si lim t→t0y(t) − Bx ...
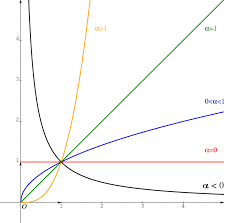 Étude de fonction et fonctions usuelles
Étude de fonction et fonctions usuelles
f(x) − ax = ±∞ : branche parabolique de direction asymptotique y = ax. Exemple 5. Déterminer les branches infinies de la fonction f définie par f(x) = 2
 Branches infinies dune fonction f
Branches infinies dune fonction f
petit par rapport à x.) c3) Branche parabolique de direction asymptotique ( ). Oy.. lim et lim. B.P. de direction ( ) x x. f x. f x. Oy x.
 I Asymptote Oblique II Branches paraboliques
I Asymptote Oblique II Branches paraboliques
II Branches paraboliques. II.1 Branche parabolique de direction (Ox). On dit que Cf présente une branche parabolique de direction asymptotique (Ox) en +?
 Vademecum sur létude des fonctions
Vademecum sur létude des fonctions
Limites et étude des branches asymptotiques aux bords du domaine de définition. branche parabolique de direction verticale.
 Chapitre 11. (Complément) sur le comportement asymptotique des
Chapitre 11. (Complément) sur le comportement asymptotique des
asymptotique des fonctions réelles possède une branche parabolique dont l'axe est donné par la direction que regarde la courbe. Plus précisément.
 Branches infinies
Branches infinies
On dit que f possède une branche infinie en a si lim ( ) est une branche parabolique horizontale. Exemples : f x.
 Etude de branches infinies. 1 Démarche
Etude de branches infinies. 1 Démarche
- Si c'est +? pas d'asymptote mais une branche parabolique d'axe oblique. 2. Page 3. 2 Exercices. Exercice 1 Étudier le comportement asymptotique des
 COURBES PARAMETREES
COURBES PARAMETREES
1 nov. 2004 on dit que la courbe admet une branche parabolique de direction asymptotique la droite vectorielle d'équation y = Bx.
 TECHNIQUES & MÉTHODES S03 ÉTUDE DE FONCTIONS
TECHNIQUES & MÉTHODES S03 ÉTUDE DE FONCTIONS
Exemple : La fonction ln x + ?2 x ? 1 présente une branche parabolique de direction asymptotique (Ox) en +?. 0. 1. 2. 3. 4. 5. 6. 7. 8.
 PERNOT MOISSON - Étude des points à linfini dune courbe
PERNOT MOISSON - Étude des points à linfini dune courbe
que le genre des branches paraboliques. I. — DIRECTION ASYMPTOTIQUE SIMPLE. Soit y— CJ = O cette direction. L'équation de la courbe est de la forme.
 Fiche méthode : Etude de fonctions
Fiche méthode : Etude de fonctions
notions : les asymptotes et les branches paraboliques. Asymptote verticale branche parabolique de direction asymptotique la droite d'équation.
 Etude des branches infinies de la courbe représentative dune fonction
Etude des branches infinies de la courbe représentative dune fonction
12 déc. 2003 direction asymptotique de Cf en x0 si limx?x0x?I. ?. ((OMx)
 [PDF] I Asymptote Oblique II Branches paraboliques - My MATHS SPACE
[PDF] I Asymptote Oblique II Branches paraboliques - My MATHS SPACE
On dit que Cf présente une branche parabolique de direction asymptotique (Ox) en +? si : asymptotique la droite d'équation y = ax en +? si :
 [PDF] Chapitre 11 (Complément) sur le comportement asymptotique des
[PDF] Chapitre 11 (Complément) sur le comportement asymptotique des
Enfin si ce même rapport tend vers l'infini on dit que la courbe possède une branche parabolique de direction l'axe des ordonnées (Oy) (ce qui est le cas de l
 [PDF] Branches infinies
[PDF] Branches infinies
La branche infinie est une asymptote horizontale d'équation y=l 2° cas : a?R l=+? La branche
 [PDF] Les branches infinies de la courbe ( )f
[PDF] Les branches infinies de la courbe ( )f
de direction : Oy ( )f C admet une branche parabolique de direction : y ax = ( ) ( )f ladroite D :y ax b est asymptote à C
 [PDF] Etude de branches infinies 1 Démarche
[PDF] Etude de branches infinies 1 Démarche
Soit lim x?+? f(x) ? ax = ±? et la courbe de f admet une branche parabolique de direction y = ax Exemples : f(x) = x +
 [PDF] Branches infinies dune fonction f
[PDF] Branches infinies dune fonction f
branche parabolique dont l'axe est donné par la direction que regarde la courbe c2) Branche parabolique de direction asymptotique ( )
 [PDF] Branches-infiniespdf - PTSI 1 Eucalyptus
[PDF] Branches-infiniespdf - PTSI 1 Eucalyptus
? ± ? le graphe de admet une branche parabolique de direction asymptotique la droite d'équation = ii Si ( ) ? ?±?
 [PDF] Vademecum sur létude des fonctions
[PDF] Vademecum sur létude des fonctions
Limites et étude des branches asymptotiques aux bords du domaine de définition branche parabolique de direction verticale
 Etude des branches infinies - Cas des courbes représentatives
Etude des branches infinies - Cas des courbes représentatives
On dit alors que Cf C f admet une branche parabolique ou encore que Cf C f admet une direction asymptotique On distingue 3 cas : a=±
 [PDF] techniques & méthodes s03 - MPSI Saint-Brieuc
[PDF] techniques & méthodes s03 - MPSI Saint-Brieuc
Branche parabolique de direction (Ox) Définition : On dit que Cf présente une branche parabolique de direction asymptotique (Ox) en +? si :
Comment déterminer la branche parabolique ?
Quand la courbe semble regarder dans une direction mais tout en s'en éloignant, on dit que la courbe poss? une branche parabolique dont l'axe est donné par la direction que regarde la courbe.Comment déterminer les branches infinies ?
Etude de branches infinies. Étant donnée une fonction f : R ?? R, l'étude de ses branches infinies a pour objectif de comprendre en détails le comportement de f(x) quand x tend vers +? ou ??. interprétation des différents résultats que l'on peut obtenir pour ce calcul.Comment montrer que Cf admet une branche parabolique ?
f(x) = l ? R, alors on dit que Cf admet une asymptote horizontale y = l au voisinage de +?. = ±?, alors on dit que Cf admet une branche parabolique de direction l'axe des ordonnées. = 0, alors on dit que Cf admet une branche parabolique de direction l'axe des abscisses.- Lorsqu'une limite à l'infini est infinie, il est possible qu'une asymptote oblique existe. Elle s'écrit sous la forme y=ax+b y = a x + b puisqu'elle est l'expression d'une droite.
COURBES PARAMETREES
P. Pansu
November 1, 2004
1 Motivation
La trajectoire d"un point qui se d´eplace dans un plan, c"estdonn´e par deux fonctionsx(t) ety(t)
du temps.2 Objectif
Lorsque les fonctionst?→x(t) ett?→y(t) sont donn´ees, on veut tracer la courbe `a la main.
On sait d´ej`a tracer des trajectoires particuli`eres, celles o`ux(t) =t. En effet, dans ce cas, la
courbe est le graphe d"une fonction d"une variable r´eelle.On va voir que le trac´e dans le cas g´en´eral
se d´eduit de ce cas particulier. Il y a deux nouveaut´es : le traitement des sym´etries, et celui des points singuliers. Notre exemple favori : la courbe d´ecrite parx(t) = sin(2t),y(t) = sin(3t) pourt?R.3 Sym´etries
Attention, il y a deux fonctions en jeu,x(t) ety(t), et non une,y=f(x). Ca change tout. Laparit´e/imparit´e des fonctionsx(t) ety(t) se traduit par exemple par les sym´etries suivantes.
•Lorsquexetysont impaires,c(-t) =-c(t) s"obtient `a partir dec(t) par une sym´etrie centrale. •Lorsquexest impaire etypaire,c(-t) s"obtient `a partir dec(t) par une sym´etrie par rapport `a l"axeOy. •Lorsquexetysont paires,c(-t) =c(t), donc la courbe revient sur ses pas. •Lorsquexest paire etyimpaire,c(-t) s"obtient `a partir dec(t) par une sym´etrie par rapport `a l"axeOx. Pas de recette `a apprendre par coeur, mais un raisonnement d"une ligne `a savoir refaire.Exemple.Dans l"exemplec(t) =?sin(2t)
sin(3t)? , la recherche de sym´etries conduit aux conclusions suivantes.Commex(t+2π) =x(t) ety(t+2π) =y(t), l"intervalle [0,2π] suffit `a param´etrer toute la courbe.
Commex(t+π) =x(t) ety(t+π) =-y(t), la portion de la courbe param´etr´ee par [π,2π]s"obtient `a partir de celle param´etr´ee par [0,π] par une sym´etrie par rapport `a l"axe 0x.
Commex(π-t) =-x(t) ety(π-t) =y(t), la portion de la courbe param´etr´ee par [π/2,π]
s"obtient `a partir de celle param´etr´ee par [0,π/2] par une sym´etrie par rapport `a l"axe 0y.
On ´etudie donc la courbe sur l"intervalle [0,π/2] et on compl`ete le trac´e par deux sym´etries.
14 Points singuliersUn pointc(t0) d"une courbecest ditsinguliersi la vitessec?(t0) = 0. On se demande quel est
l"aspect de la courbe au voisinage d"un point singulier. Pour cela, on utilise des d´eveloppements
limit´es. On pourra d´ecrire l"aspect de la courbe sous l"hypoth`ese que les d´eveloppements limit´es
n´ecessaires poss`edent des termes non nuls. Pour all´eger les notations, on supposera toujours quet0= 0.4.1 Proc´ed´e pratique
On suppose quec(t) poss`ede un d´eveloppement limit´e de la forme c(t) =c(0) +tav1+tbv2+tb?(t), o`ua < betv1etv2sontlin´eairement ind´ependants.Alors labranche sortante, i.e. pourtpositif petit, est contenue dans le quadrant d´elimit´e par
v1etv2et tangente `av2.
Labranche entrante, i.e. pourtn´egatif petit, est aussi tangente `av1, mais contenue dans l"un des 4 quadrants d´efinis parv1etv2. Lequel ? Cela d´epend des signes detaet detbpourt <0, i.e. de la parit´e deaet deb. 2vv 12vv 12vv 12vv 1On peut justifier le trac´e comme suit : il existe un changement de coordonn´ees tel que, dans les
nouvelles coordonn´ees, la branche sortante ait pour ´equationY=Xb/a. Dans le dernier cas, cela
ne suffit pas `a compl´eter le trac´e. Pour d´ecider si la branche entrante est plus proche ou moins
proche dev1que la branche sortante, il faut pousser le d´eveloppement limit´e plus loin, jusqu"`a ce
qu"un terme entc,cimpair, apparaisse.4.2 Terminologie
La terminologie suivante doit ˆetre connue.
D´efinition 11. Siaest pair etbimpair, on parle depoint de rebroussement de premi`ere esp`ece. Dans ce cas, la courbe poss`ede une demi-tangente de vecteur directeurv1.2. Siaest impair etbimpair, on parle depoint d"inflexion. Dans ce cas, la courbe poss`ede une
tangente de vecteur directeurv1.3. Siaest impair etbpair, on parle depoint ordinaire. Dans ce cas, la courbe poss`ede une
tangente de vecteur directeurv1.4. Siaest pair etbimpair, on parle depoint de rebroussement de deuxi`eme esp`ece. Dans ce
cas, la courbe poss`ede une demi-tangente de vecteur directeurv1. Exemple.Etude du point singulier ent= 0 de la courbe param´etr´ee parx(t) =t2,y(t) =t2+t3.Le d´eveloppement limit´e
c(t) =t2?12? +t3?01? +t3?(t) montre qu"il s"agit d"un point de rebroussement de premi`ere esp`ece. La courbe poss`ede une demi- tangente de vecteur directeur?12? 0.04 0.02Page 1
Rebroussement de premi`ere esp`ece
Exemple.Etude du point singulier ent= 0 de la courbe param´etr´ee parx(t) =-t3+t4, y(t) =t3.Le d´eveloppement limit´e
c(t) =t3?-1 1? +t4?10? +t4?(t) montre qu"il s"agit d"un point ordinaire, avec tangente de vecteur directeur?-1 1?0.20.1-0.1-0.20.2
0.1 -0.1 -0.2Page 1
Point ordinaire
Exemple.Etude locale de la courbe param´etr´ee d´efinie parx(t) = 3(sin(t)-t),y(t) =t3+t5.Le d´eveloppement limit´e
c(t) =t3?-1 21?+t5?1401? +t5?(t), montre qu"il s"agit d"un point d"inflexion, de tangente de vecteur directeur?-1 21?
0.20.1-0.1-0.20.2
0.1 -0.1 -0.2Page 1
Point d"inflexion
Exemple.Etude locale de la courbe param´etr´ee d´efinie parx(t) = 3(cos(t)-1),y(t) =t2+t4+t5.
Le d´eveloppement limit´e
c(t) =t2?3 21?+t4?-181? +t4?(t), montre qu"il s"agit d"un point de rebroussement de deuxi`eme esp`ece, de demi-tangente de vecteur directeur? 3 21?
-0.2-0.4-0.6-0.81 0.8 0.6 0.4 0.2
Page 1
Point de rebroussement de deuxi`eme esp`ece
5 Branches infiniesOn parle debranche infinielorsquettend verst0(´eventuellementt0=±∞) si l"une des fonction
x(t) ety(t) n"est pas born´ee au voisinage det0.Comme dans le cas des courbes repr´esentatives de fonctions, on dira qu"une courbe param´etr´ee
admet pourasymptotela droite d"´equationAx+By+C= 0 lorsquettend verst0(´eventuellement a=±∞) si l"une des fonctionx(t) ety(t) n"est pas born´ee au voisinage det0et si lim t→t0Ax(t) +By(t) +C= 0. Si|y(t)|tend vers l"infini etx(t) poss`ede une limite finieC, alors la droite affine d"´equation x-C= 0 est asymptote `a la courbe.Sinon, pour d´eceler la pr´esence d"une ´eventuelle asymptote pourtvoisin det0, on ´etudie le
rapport y(t) x(t). Si lim t→t0y(t) x(t)= +∞, on dit que la courbe admet unebranche parabolique de direction asymptotiqueOy. S"il admet une limite finieB, on ´etudie la diff´erencey(t)-Bx(t). Si limt→t0y(t)-Bx(t) =±∞, on dit que la courbe admet unebranche parabolique de direction asymptotique la droite vectorielle d"´equationy=Bx. Si limt→t0y(t)-Bx(t) =C est finie, on conclut que la droite affine d"´equationy-Bx-C= 0 est asymptote `a la courbe. Exemple.Etude des branches infinies de la courbe param´etr´ee d´efinie parx(t) =-4t2+ 4t, y(t) = 3t3-t.Comme lim
t→±∞y(t)/x(t) =?∞, la courbe pr´esente des branches paraboliques de directionOy.
Exemple.Etude des branches infinies de la courbe param´etr´ee d´efinie parx(t) = tan(t)+sin(t)
ety(t) = 1/cos(t).Par p´eriodicit´e, on peut prendret?[-π,π[. Les branches infinies correspondent aux valeurs de
tpour lesquellesx(t) ouy(t) n"est pas d´efini, soitt=-π/2 ett=π/2. Pourtvoisin deπ/2, les deux coordonn´ees tendent vers l"infini. Le rapporty(t)/x(t) = sint(1 + cost) tend vers 1. La diff´erencey(t)-x(t) = sint+ (sint-1)/costtend vers 1 donc la droite d"´equationy=x+ 1 est asymptote `a la courbe. Ent=-π/2, on trouve pour asymptote la droite d"´equationy=-x-1.6 Tableau de variation
Une fois d´etermin´ees les sym´etries, qui permettent de r´eduire l"intervalle d"´etude de la courbe, les
natures des points singuliers et des branches infinies, il nereste plus qu"`a ´etudier les variations des
fonctionsx(t) ety(t). En effet, cela permet de placer les points remarquables, `asavoir les pointssinguliers et les points o`u la tangente est parall`ele `a l"un des axes de coordonn´ees. Entre deux
valeurs remarquables, le vecteur vitesse pointe dans un quadrant constant (NE, NO, SO, SE), et il suffit de respecter cette r`egle pour obtenir un trac´e satisfaisant. Exemple.Etude de la courbe param´etr´ee d´efinie parx(t) =-4t2+ 4t,y(t) = 3t3-t.Tableau de variations :
t01/31/21 x"4+4/3+0--4 x0?8/9?1?0 y"-1-0+5/4--8 y0?-2/9?-1/8?2 On place d"abord les points et les tangentes correspondant aux valeurst= 0, 1/3, 1/2 et 1.Puis on compl`ete le dessin.
±2±1012
y ±1±0.8 ±0.6±0.4±0.2 0.20.40.6 0.81x
Exemple.Tracer la courbe d´ecrite parx(t) = sin(2t),y(t) = sin(3t) pourt?R.Comme vu plus haut, on ´etudie la courbe sur l"intervalle [0,π/2] et on compl`ete le trac´e par deux
sym´etries.Tableau de variations :
t0π/6π/4π/2 x"2+1+0--1 x0?⎷3/2?1?0 y"3+0-3⎷2/2-0 y0?1?⎷2/2?-1 On place d"abord les points et les tangentes correspondant aux valeurst= 0,π/6,π/4 etπ/2. Puis on relie ces points par des arcs ayant la bonne orientation, et on compl`ete le dessin par deux sym´etries.±1±0.50.5
1 ±1±0.50.51
L"´etude des variations dex(t) ety(t) r´ev`ele un point singulier ent=π. Les d´eveloppements
limit´es en fonction des=t-π x(t) =12s3+s3?(s), y(t) =-1-12s2+s3?(s)
montrent que le point singulier est un rebroussement de premi`ere esp`ece, avec demi-tangente verticale. x21-1-2y2 1 -1 -2Page 1
-0.92 -0.94 -0.96 -0.98 -1 -1.02 -1.04 -1.06 -1.08 Page 1Vue d"ensemble avec les asymptotes Zoom au point singulierquotesdbs_dbs13.pdfusesText_19[PDF] etudes des fonctions branches infinies
[PDF] mode d'emploi lave linge brandt
[PDF] comment utiliser machine a laver brandt
[PDF] bras de levier définition
[PDF] levier inter appui
[PDF] cours moment d'une force par rapport ? un axe
[PDF] bras de levier calcul
[PDF] moment d'une force cours
[PDF] moment d'une force par rapport ? un axe pdf
[PDF] moment de force exercice
[PDF] moment d'un couple de force
[PDF] brassage interchromosomique et intrachromosomique animation
[PDF] brassage allélique définition
[PDF] definition brassage allelique
