 I Asymptote Oblique II Branches paraboliques
I Asymptote Oblique II Branches paraboliques
II Branches paraboliques. II.1 Branche parabolique de direction (Ox). On dit que Cf présente une branche parabolique de direction asymptotique (Ox) en +∞ si :.
 Chapitre 11. (Complément) sur le comportement asymptotique des
Chapitre 11. (Complément) sur le comportement asymptotique des
est 0 on dit que la courbe possède une branche parabolique de direction l'axe des abscisses (Ox) (c'est le cas en particulier du logarithme). Enfin
 Etude de branches infinies. 1 Démarche
Etude de branches infinies. 1 Démarche
- Si c'est +∞ pas d'asymptote mais une branche parabolique d'axe oblique. 2. Page 3. 2 Exercices. Exercice 1 Étudier le comportement asymptotique des
 Branches infinies
Branches infinies
la branche infinie est une branche parabolique horizontale. Exemples : f x x. ( ) =
 Exemples à connaître de branches infinies
Exemples à connaître de branches infinies
On dit qu'il y a une direction asymptotique verticale. Il y a même une branche parabolique verticale (c'est-à-dire qu'il y a une direction mais l'écart
 Etude des branches infinies de la courbe représentative dune fonction
Etude des branches infinies de la courbe représentative dune fonction
12 déc. 2003 ... direction asymptotique en x0. ... – cette limite existe et appartient `a {+∞−∞}
 PERNOT MOISSON - Étude des points à linfini dune courbe
PERNOT MOISSON - Étude des points à linfini dune courbe
— DIRECTION ASYMPTOTIQUE SIMPLE. Soit y— CJ = O cette direction. L'équation forme de la branche parabolique à étudier. On peut écrire. <p»-i(tf
 COURBES PARAMETREES
COURBES PARAMETREES
1 nov. 2004 on dit que la courbe admet une branche parabolique de direction asymptotique la droite vectorielle d'équation y = Bx. Si lim t→t0y(t) − Bx ...
 Étude de fonction et fonctions usuelles
Étude de fonction et fonctions usuelles
f(x) − ax = ±∞ : branche parabolique de direction asymptotique y = ax. Exemple 5. Déterminer les branches infinies de la fonction f définie par f(x) = 2
 Branches infinies dune fonction f
Branches infinies dune fonction f
petit par rapport à x.) c3) Branche parabolique de direction asymptotique ( ). Oy.. lim et lim. B.P. de direction ( ) x x. f x. f x. Oy x.
 I Asymptote Oblique II Branches paraboliques
I Asymptote Oblique II Branches paraboliques
II Branches paraboliques. II.1 Branche parabolique de direction (Ox). On dit que Cf présente une branche parabolique de direction asymptotique (Ox) en +?
 Vademecum sur létude des fonctions
Vademecum sur létude des fonctions
Limites et étude des branches asymptotiques aux bords du domaine de définition. branche parabolique de direction verticale.
 Chapitre 11. (Complément) sur le comportement asymptotique des
Chapitre 11. (Complément) sur le comportement asymptotique des
asymptotique des fonctions réelles possède une branche parabolique dont l'axe est donné par la direction que regarde la courbe. Plus précisément.
 Branches infinies
Branches infinies
On dit que f possède une branche infinie en a si lim ( ) est une branche parabolique horizontale. Exemples : f x.
 Etude de branches infinies. 1 Démarche
Etude de branches infinies. 1 Démarche
- Si c'est +? pas d'asymptote mais une branche parabolique d'axe oblique. 2. Page 3. 2 Exercices. Exercice 1 Étudier le comportement asymptotique des
 COURBES PARAMETREES
COURBES PARAMETREES
1 nov. 2004 on dit que la courbe admet une branche parabolique de direction asymptotique la droite vectorielle d'équation y = Bx.
 TECHNIQUES & MÉTHODES S03 ÉTUDE DE FONCTIONS
TECHNIQUES & MÉTHODES S03 ÉTUDE DE FONCTIONS
Exemple : La fonction ln x + ?2 x ? 1 présente une branche parabolique de direction asymptotique (Ox) en +?. 0. 1. 2. 3. 4. 5. 6. 7. 8.
 PERNOT MOISSON - Étude des points à linfini dune courbe
PERNOT MOISSON - Étude des points à linfini dune courbe
que le genre des branches paraboliques. I. — DIRECTION ASYMPTOTIQUE SIMPLE. Soit y— CJ = O cette direction. L'équation de la courbe est de la forme.
 Fiche méthode : Etude de fonctions
Fiche méthode : Etude de fonctions
notions : les asymptotes et les branches paraboliques. Asymptote verticale branche parabolique de direction asymptotique la droite d'équation.
 Etude des branches infinies de la courbe représentative dune fonction
Etude des branches infinies de la courbe représentative dune fonction
12 déc. 2003 direction asymptotique de Cf en x0 si limx?x0x?I. ?. ((OMx)
 [PDF] I Asymptote Oblique II Branches paraboliques - My MATHS SPACE
[PDF] I Asymptote Oblique II Branches paraboliques - My MATHS SPACE
On dit que Cf présente une branche parabolique de direction asymptotique (Ox) en +? si : asymptotique la droite d'équation y = ax en +? si :
 [PDF] Chapitre 11 (Complément) sur le comportement asymptotique des
[PDF] Chapitre 11 (Complément) sur le comportement asymptotique des
Enfin si ce même rapport tend vers l'infini on dit que la courbe possède une branche parabolique de direction l'axe des ordonnées (Oy) (ce qui est le cas de l
 [PDF] Branches infinies
[PDF] Branches infinies
La branche infinie est une asymptote horizontale d'équation y=l 2° cas : a?R l=+? La branche
 [PDF] Les branches infinies de la courbe ( )f
[PDF] Les branches infinies de la courbe ( )f
de direction : Oy ( )f C admet une branche parabolique de direction : y ax = ( ) ( )f ladroite D :y ax b est asymptote à C
 [PDF] Etude de branches infinies 1 Démarche
[PDF] Etude de branches infinies 1 Démarche
Soit lim x?+? f(x) ? ax = ±? et la courbe de f admet une branche parabolique de direction y = ax Exemples : f(x) = x +
 [PDF] Branches infinies dune fonction f
[PDF] Branches infinies dune fonction f
branche parabolique dont l'axe est donné par la direction que regarde la courbe c2) Branche parabolique de direction asymptotique ( )
 [PDF] Branches-infiniespdf - PTSI 1 Eucalyptus
[PDF] Branches-infiniespdf - PTSI 1 Eucalyptus
? ± ? le graphe de admet une branche parabolique de direction asymptotique la droite d'équation = ii Si ( ) ? ?±?
 [PDF] Vademecum sur létude des fonctions
[PDF] Vademecum sur létude des fonctions
Limites et étude des branches asymptotiques aux bords du domaine de définition branche parabolique de direction verticale
 Etude des branches infinies - Cas des courbes représentatives
Etude des branches infinies - Cas des courbes représentatives
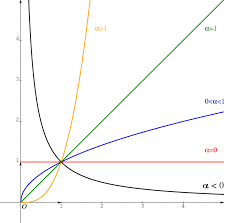
On dit alors que Cf C f admet une branche parabolique ou encore que Cf C f admet une direction asymptotique On distingue 3 cas : a=±
 [PDF] techniques & méthodes s03 - MPSI Saint-Brieuc
[PDF] techniques & méthodes s03 - MPSI Saint-Brieuc
Branche parabolique de direction (Ox) Définition : On dit que Cf présente une branche parabolique de direction asymptotique (Ox) en +? si :
Comment déterminer la branche parabolique ?
Quand la courbe semble regarder dans une direction mais tout en s'en éloignant, on dit que la courbe poss? une branche parabolique dont l'axe est donné par la direction que regarde la courbe.Comment déterminer les branches infinies ?
Etude de branches infinies. Étant donnée une fonction f : R ?? R, l'étude de ses branches infinies a pour objectif de comprendre en détails le comportement de f(x) quand x tend vers +? ou ??. interprétation des différents résultats que l'on peut obtenir pour ce calcul.Comment montrer que Cf admet une branche parabolique ?
f(x) = l ? R, alors on dit que Cf admet une asymptote horizontale y = l au voisinage de +?. = ±?, alors on dit que Cf admet une branche parabolique de direction l'axe des ordonnées. = 0, alors on dit que Cf admet une branche parabolique de direction l'axe des abscisses.- Lorsqu'une limite à l'infini est infinie, il est possible qu'une asymptote oblique existe. Elle s'écrit sous la forme y=ax+b y = a x + b puisqu'elle est l'expression d'une droite.
Fiche m´ethode : Etude de fonctions
Le plan d"´etude d"une fonction est comme suit : 1Ensemble de d´efinition, ensemble d"´etude
2Etude de la continuit´e (si n´ecessaire)
3 Etude de la d´erivabilit´e (si n´ecessaire) 4Etude des variations
5 Etude des limites aux bornes de l"ensemble de d´efinition 6Trac´e de la courbe repr´esentative Γf.
Partie I.Domaine de d´efinition et domaine d"´etudeI-1.Domaine de d´efinition
La fonction `a ´etudier est construite par op´erations `a partir de fonctions usuelles. Vous en d´eduisez
le domaine de d´efinitionDfdef. En g´en´eral, les th´eor`emes "OPA" sur les fonctions continues ou
d´erivables permettent directement de conclure quant `a lacontinuit´e et `a la d´erivabilit´e def.
Exemple :f(x) = ln[x(x-1)] est d´efinie et de classeC∞sur ]- ∞,0[?[1,+∞[.I-2.Domaine d"´etude
LorsquefestT-p´eriodique, on peut restreindre l"´etude `a un intervalle de longueurT, par exemple
D f∩[0,T[, et compl´eter par sym´etrie.Il est possible de restreindre le domaine d"´etude lorsquefest paire ou impaire. Plus g´en´eralement,
s"il existea?Dftel que ?si pour toutx,f(2a-x) =f(x), alors la droite d"´equationx=aest axe de sym´etrie de Γf. On peut restreindre l"´etude `aDf∩[a,+∞[ et compl´eter ensuite par sym´etrie. ?si pour toutx,f(2a-x) = 2f(a)-f(x), alors le pointA?a f(a)? est centre de sym´etrie de Γ f. On peut restreindre l"´etude `aDf∩[a,+∞[ et compl´eter ensuite par sym´etrie. Exemple :La fonctionf(x) = sin2xcos2xest de classeC∞surRpar op´erations alg´ebriques. De plus,fest paire etπ-p´eriodique. On restreint l"´etude `a [0,π/2]. Partie II.Etude de la continuit´e aux points particuliersParfois les th´eor`emes "OPA" sur les fonctions continues ne permettent pas de conclure. Des ´etudes
particuli`eres sont alors n´ecessaires.C"est le cas, notamment, lorsque la fonctionfest d´efinie par des expressions diff´erentes `a gauche et
`a droite d"un pointa. Exemple :Soitf:R→Rd´efinie parf(0) = 0, et pour toutx?R?,f(x) =?x(1-lnx) six >0 xln(1-1/x) six <0 En ce cas, vous utilisez les limites `a droite et `a gauche :Proposition.-sifest d´efinie au pointa.
limx→af(x) =f(a)???lim
x→a-f(x) =f(a)lim
x→a+f(x) =f(a) Exercice 1 :Etudiez la continuit´e de la fonctionf:R→Rd´efinie par pour toutx?R, f(x) =?x?+? x- ?x?Partie III.Etude de la d´erivabilit´e
Comme pour la continuit´e, la question est souvent r´egl´eepar OPA sur des fonctions d´erivables.
N´eanmoins, une ´etude particuli`ere est parfois n´ecessaire. Pour ´etudier la d´erivabilit´e en un pointadu domaine de d´efinition, vous pouvez revenir `a la d´efinition et ´etudier la limite des taux de variationsf(x)-f(a) x-a´etudier les d´eriv´ees `a gauche et `a droite au pointa: lorsqu"elles existent et sont finies, il s"agit
des limites : f ?g(a) = lim x→a-f(x)-f(a) x-aetf?d(a) = lim x→a+f(x)-f(a)x-a Proposition.-S"il existed?Rtel quef?g(a) =f?d(a) =d,alors fest d´erivable au pointaetf?(a) =d.Vocabulaire :Sif?g(a)etf?d(a)existent mais sont diff´erentes, on dit que le graphe defpr´esente un
point anguleux. Exercice 2 :Etudiez la d´erivabilit´e def(x) =? x3(2-x). 2Th´eor`eme.- condition suffisante de d´erivabilit´eSoitfune fonction d´erivable d´erivable dansI\ {a}.
S"il existed?Rtel que limx→aPartie IV.Variations
Vous r´esolvez l"in´equationf?(x)≥0, et non pas l"´equationf(x) = 0 Vous en d´eduisez, grˆace aux
liens avec la monoonie les variations def. Vous pr´esentez ces r´esultats sous forme d"un tableau de variations.Exercice 3 :Etudiez les variations def(x) =x+?
3x(8-x).
Partie V.Etude aux bornes du domaine
V-1.D´efinitions
L"´etude des branches infinies sert `a pr´eciser l"allure dela courbe repr´esentative d"une fonction au
voisinage des bornes du domaiie. Ces bornes peuvent ˆetre r´eelles ou infinies. Nous distinguons deux
notions : les asymptotes et les branches paraboliques.Asymptote verticale
Siaest une borne r´eelle du domaine de d´efinition, le graphe defpeut pr´esenter un point d"arrˆet
ou une asymptote verticale. Il s"agit d"´etudier limx→af(x), o`uaest une borne r´eelle du domaine de
d´efinition. On suppose de plus quefn"est pas d´efinie au pointa.D´efinition :S"il existe un nombre r´eel??Rtel quelimx→af(x) =?, on dit quefest prolongeable par
continuit´e au pointa. Le graphe defpr´esente alors unpoint d"arrˆetenA(a,?). 3 D´efinition :On dit que la droite d"´equationx=aestasymptote verticale`aCfsilimx→af=±∞. Exemple :La fonction ln(x-2)+xsinxadmet la droite d"´equation x= 2 comme asymptote verticale.±10±8±6±4±202468
Supposons d´esormais que +∞est une borne du domaine de d´efinition. Au voisinage de +∞, le
graphe defpeut pr´esenter une asymptote (horizontale ou oblique), ouune branche parabolique.Asymptote horizontale
D´efinition :On dit que la droite d"´equationy=?estasymptote horizontaleen+∞`aCfsilimx→+∞f(x) =?. On dit que la droite d"´equationy=?estasymptote horizontale en-∞`aCfsilimx→-∞f(x) =?.Exemple :La fonction 5-exp(-x+⎷
3x+ 1) admet la droite
d"´equationy= 5 comme asymptote horizontale en +∞.012345678
1 2 3 4 5 6 7
Asymptote oblique
D´efinition :On dit que la droite d"´equationy=a x+b(a?R?, b?R) estasymptote obliqueen+∞`aCfsilimx→+∞?f(x)-ax- b?= 0. On dit que la droite d"´equationy=a x+b(?R?etb?R) est asymptote obliqueen-∞`aCfsilimx→-∞?f(x)-ax-b?= 0.Exemple :La fonction 2 +1
2x+ 5x2(x-2) exp(-x) admet la
droite d"´equationy= 2 +12xcomme asymptote oblique en +∞.
012345678
y1 2 3 4 5 6 7
xBranche parabolique de direction(Ox)
D´efinition :On dit queCfpr´esente unebranche parabolique de direction asymptotique(Ox)en+∞si :limx→+∞f(x) =±∞.
limx→+∞f(x)
x= 0Exemple :La fonction lnx+⎷
2x-1 pr´esente une branche para-
bolique de direction asymptotique (Ox) en +∞.012345678
y1 2 3 4 5 6 7
x 4Branche parabolique de direction(Oy)
D´efinition :On dit queCfpr´esente unebranche parabolique de direction asymptotique(Oy)en+∞si :limx→+∞f(x) =±∞.
limx→+∞f(x)
x=±∞Exemple :La fonction 1-⎷
x+x22pr´esente une branche parabo- lique de direction asymptotique (Oy) en +∞.012345678
y1 2 3 4 5 6 7
x Branche parabolique de direction la droite d"´equationy=ax D´efinition :On dit queCfpr´esente unebranche parabolique de direction asymptotique la droite d"´equationy=axen +∞si :limx→+∞f(x)
x=a.limx→+∞f(x)-ax=±∞
Exemple :Le graphe de la fonctionx
2+⎷2x-2 pr´esente une
branche parabolique de direction asymptotique la droite d"´equation y=12xen +∞.
012345678
y2 4 6 8 10 12
xV-2.Recherche des branches infinies
Pour l"´etude des branches infinies, pensez avant tout `a utiliser les d´efinitions, car l"´enonc´e vous
guide souvent. Si ce n"est pas le cas, vous proc´edez de la mani`ere suivante : Au voisinage d"un pointa?¯I(une borne r´eelle de l"intervalle) : ?si limx→af(x) =±∞, la droite d"´equationx=aest asymptote verticale. Au voisinage d"une borne infinie de l"intervalle, par exemple +∞: ?Si limx→+∞f(x) =??R, la droite d"´equationy=?est asymptote horizontale. Si limx→+∞f(x) =±∞, il faut poursuivre l"analyse ... ?Si limx→+∞f(x) x= 0, la courbe pr´esente une branche parabolique de direction asympto- tique (Ox) ?Si limx→+∞f(x) x=±∞, la courbe pr´esente une branche parabolique de direction asymp- totique (Oy)Si limx→+∞f(x)
x=a?R?, il faut poursuivre l"analyse ... ?Si limx→+∞f(x)-ax=±∞, la courbe pr´esente une branche parabolique de direction asymptotique la droite d"´equationy=ax ?Si limx→+∞f(x)-ax=b?R, la droite d"´equationy=ax+best asymptote `a la courbe. Exercice 4 :Recherchez les asymptotes obliques de courbe d"´equation cart´esienney=⎷ x2+ 3x+ 2.Partie VI.Trac´e de la courbe
La figure doit comporter les tangentes horizontales, les tangentes particuli`eres, les asymptotes.Partie VII.Exercices
Exercice 5 :Etudiez et repr´esentez
1.f(x) =⎷
x2+ 3x-4.2.f(x) = sin2x+ cosx.
3.f(x) =x+ ln(1 +ex).
6quotesdbs_dbs13.pdfusesText_19[PDF] etudes des fonctions branches infinies
[PDF] mode d'emploi lave linge brandt
[PDF] comment utiliser machine a laver brandt
[PDF] bras de levier définition
[PDF] levier inter appui
[PDF] cours moment d'une force par rapport ? un axe
[PDF] bras de levier calcul
[PDF] moment d'une force cours
[PDF] moment d'une force par rapport ? un axe pdf
[PDF] moment de force exercice
[PDF] moment d'un couple de force
[PDF] brassage interchromosomique et intrachromosomique animation
[PDF] brassage allélique définition
[PDF] definition brassage allelique
