[PDF] Intégration et primitive Intégration et primitive. 1

View - Download Intégration et primitive

Previous PDF

Next PDF

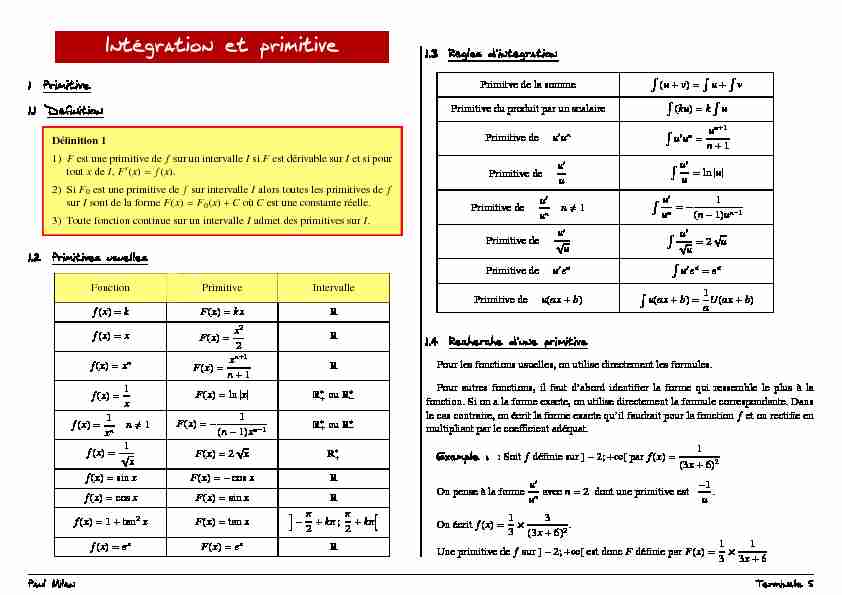
Intégration et primitive

1 Pri mitive 1.1 Dé finition

Définition 1

1

1)Fest une primitive defsur un intervalleIsiFest dérivable surIet si pour

toutxdeI,F?(x)=f(x).

2) SiF0est une primitive defsur intervalleIalors toutes les primitives def

surIsont de la formeF(x)=F0(x)+CoùCest une constante réelle.

3) Toute fonction continue sur un intervalleIadmet des primitives surI.

1.2 Pri mitives usuelles

Fonction

Primitive

Intervalle

f(x)=k

F(x)=kx

R f(x)=x

F(x)=x2

2 R f(x)=xn

F(x)=xn+1

n+1 R f(x)=1 x

F(x)=ln|x|

R?+ouR?-

f(x)=1 xnn?1

F(x)=-1

(n-1)xn-1

R?+ouR?-

f(x)=1 ⎷x

F(x)=2⎷

x R?+ f(x)=sinx

F(x)=-cosx

R f(x)=cosx

F(x)=sinx

R f(x)=1+tan2x

F(x)=tanx

2+kπ;π

2+kπ?

f(x)=ex

F(x)=ex

R 1.3

Règles

d"in té gra tion

Primitve de la somme

?(u+v)=?u+?v

Primitive du produit par un scalaire

?(ku)=k?u

Primitive deu?un

?u?un=un+1 n+1

Primitive deu?

u ?u? u=ln|u|

Primitive deu?

unn?1 ?u?un=-1 (n-1)un-1

Primitive deu?

⎷u ?u? ⎷u=2⎷ u

Primitive deu?eu

?u?eu=eu

Primitive deu(ax+b)

?u(ax+b)=1 aU(ax+b) 1.4 Re cherche d"une pri mitive Pour les fonctions usuelles, on utilise directement les formules. Pour autres fonctions, il faut d'abord identifier la forme qui ressemble leplus à la fonction. Si on a la forme exacte, on utilise directement la formule correspondante. Dans le cas contraire, on écrit la forme exacte qu'il faudrait pour la fonctionfet on rectifie en multipliant par le coefficient adéquat. Exemple :: Soitfdéfinie sur ]-2;+∞[ parf(x)=1 (3x+6)2

On pense à la forme

u? unavecn=2 dont une primitive est-1 u.

On écritf(x)=1

3×3

(3x+6)2. Une primitive defsur ]-2;+∞[ est doncFdéfinie parF(x)=1

3×1

3x+6

Paul MilanTerminale S

2.3 Va leur moyenne 2

Inté

gra tion 2.1 Dé finition

Définition 2

1

Soitfune fonction continue sur un intervalleI:

2Pour tousaetbdeI,?

b a f(x)dx=[F(x)]ba=F(b)-F(a) oùFest une primitive defsurI.

2Pour toutadeI, la fonctionFdéfinie parF(x)=?

x a f(t)dtest la primi- tive defsurIqui s'annule pourx=a.

Exemple :?

e 1lnx xdx=?ln2x 2? e

1=ln2e

2-ln21

2=1 2 2.2 Pro prié tés

Propriété 1

1 2? a a f(x)dx=0 et? a b f(x)dx=-? b a f(x)dx

2relation de Chasles?

c a f(x)dx=? b a f(x)dx+? c b f(x)dx

2Linéarité?

b a (af(x)+bg(x))dx=a? b a f(x)dx+b? b a g(x)dx

2Sif(x)?0 sur [a,b] alors?

b a f(x)dx?0

2Sif(x)?g(x) sur [a,b] alors?

b a f(x)dx?? b a g(x)dx

2Inégalité de la moyenne :

Sim?f(x)?Msur [a;b] alorsm(b-a)??

b a f(x)dx?M(b-a) 2.3 Va leur moyenne

Définition 3

1 Sifest continue sur [a;b], la valeur moyenneμdefsur [a;b] est égale à :

μ=1

b-a? b a f(x)dx 2.4

Inté

gra tion par par tie Théorème 1SoituetvdeuxfonctionsdérivablessurItellesqueu?etv?soient continues surI. Alors : b a u(x)v?(x)dx=[u(x)v(x)]ba-? b a u?(x)v(x)dx Remarque :Si la fonction à intégrer est de la forme (ax+b)exou (ax+b)sinx, il est conseillé de prendreu(x)=ax+b.

Exemple :

Déterminer l'intégrale :I=?

1 0 xe-xdx u(x)=x u?(x)=1 v ?(x)=e-xv(x)=-e-x

I=?-xe-x?10-?

1 0 -e-xdx ?-xe-x?10-[e-x]10 =(-e-1-0)-(e-1-1) =1-2e-1 Remarque :Parfois, avec la fonction ln, on doit créer un produit.

Exemple :

Déterminer l'intégrale :J=?4

1lnxdx

u(x)=lnx u?(x)=1 x v ?(x)=1v(x)=x

J=[xlnx]41-?

4 1 1dx [xlnx]41-[x]41 =(4ln4-0)-(4-1) =8ln2-3

Paul MilanTerminale S

quotesdbs_dbs29.pdfusesText_35

[PDF] Démonstration de la formule de conjugaison pour les dioptres

[PDF] La théorie de la relativité générale - UdPPC

[PDF] Méthode de contrôle du carburateur - Honda Engines

[PDF] France métropolitaine Septembre 2013 - Math France

[PDF] Démontrer qu 'un point est le milieu d 'un segment Démontrer que

[PDF] propriétés collège

[PDF] fonctions de reference - Maths-et-tiques

[PDF] Triangles isométriques - Labomath

[PDF] lien de parenté entre l 'homme et les singes - Académie de Clermont

[PDF] Nombres complexes - Logamathsfr

[PDF] Polynésie septembre 2015 Enseignement de spécialité - Math France

[PDF] Inspiré du brevet Métropole Juin 2008 Sur la figure ci-dessous, les

[PDF] Correction Baccalauréat S - Obligatoire Métropole - Jeudi 20 Juin

[PDF] Statistiques statophobes

[PDF] Dénombrement des germes totaux et des bactéries conformes - Hal