[PDF] Suites f-définies par récurrence Sommaire

View - Download Suites f-définies par récurrence Sommaire

Previous PDF

Next PDF

PCSI3LycéeSainte-Geneviève

2020/20218 janvier 2021

Suitesf-définies par récurrencex

IyRy=xC

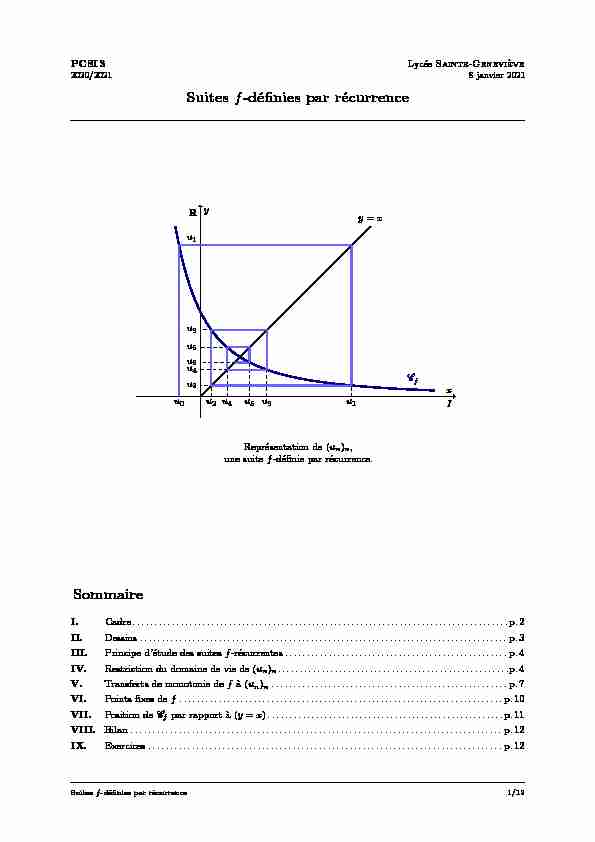
fu 0u 1u 1u 2u 2u 3u 3u 4u 4u 5u 5u

6Représentation de(un)n,

une suitef-définie par récurrence.

Sommaire

II.Dessins .................................................................................... p.3

III.Principe d"étude des suitesf-récurrentes ................................................... p.4

IV.Restriction du domaine de vie de(un)n.....................................................p.4 V.Transferts de monotonie defà(un)n...................................................... p.7 VI.Points fixes def.......................................................................... p.10 VII.Position deCfpar rapport à(y=x)......................................................p.11

VIII.Bilan ..................................................................................... p.12

IX.Exercices ................................................................................. p.12Suitesf-définies par récurrence1/12

I.Cadre

Dans tout ce qui suit, on fixe :

•Iun intervalle deR; •f:I-→Rune fonction; •(un)n>0?RNune suite réelle.Définition 1 On dit quela suite(un)nestf-définie par récurrencessi Δ ?n?N, un+1=f(un).Exemples et non-exemples

La suite(un)ndéfinie par(

u 0= 1

8n2N;un+1=p1 +un

est une suitef-définie par récurrence pour la fonctionf:x7!p1 +x.

De même, la suite(un)ndéfinie par

u 0= 1

8n2N;un+1=u2n+ 1

est une suitef-définie par récurrence pour la fonctionf:x7!1 +x2. Attentionaupiègeclassiquesuivant : la suite(un)ndéfinie par u 0= 1

8n2N;un+1=pn+unn"est pas

n"est pasn"est pasn"est pasn"est pasn"est pasn"est pasn"est pasn"est pasn"est pasn"est pasn"est pasn"est pasn"est pasn"est pasn"est pasn"est pas une suitef-définie par récurrence.

En effet, l"expression donnantun+1dépend deunmais aussi den.Dans toute la suite, on suppose que la suite(un)n>0estf-définie par récurrence.Remarque

En fait, dans la définition, plus précisément et plus exactement, il faudrait dire

8n2N;un2Ietun+1=f(un).Suitesf-définies par récurrence2/12

II.Dessins

1.

Cas cro issantIl est fondamental de pouvoir représenterCfet la suitef-définie par récurrence.

Dans le cas croissant, on a un escalier.x

IyRy=xC

fu 0u 1u 1u 2u 2u 3u 3u

42.Cas d écroissant

Dans le cas décroissant, on a un escargot.

x

IyRy=xC

fu 0u 1u 1u 2u 2u 3u 3u 4u 4u 5u 5u

6Suitesf-définies par récurrence3/12

III.Princip ed"étude des suites f-récurrentes •Pour étudier(un)n, on étudie la fonctionf. •Les propriétés defvont se transférer à la suite(un)n.

•Dans les preuves, passer d"une propriété defà une propriété de(un)nse fera toujours par récurrence

facile. C"est métamathématiquement logique puisque la suite(un)nest elle-même définie par récurrence.Les propriétés defse transfèrent à(un)n.

Se faire une idée rapide et précise de l"allure deCfpeut être très utile. On peut ensuite démontrer ce qu"on veut sur(un)n en faisant des petites récurrences.IV.Res trictiondu domaine de vie de (un)n 1.

B onnedéfinition de la suite

a)

Problématique

Sia?I, il n"est pas toujous vrai qu"il existe une suitef-définie par récurrence(un)n>0telle queu0=a.

En effet, il est possible qu"en itérant la fonctionf, on sorte du domaine def.

Par exemple, si on considère la fonction

f:?R +//R x //⎷x-1 et qu"on part deu0:= 2, alors on aura : u

1=f(u0) =f(2) =⎷2-1

etu2=f(u1) =f?⎷2-1? =?⎷2-1-1.

Or, comme

⎷2-1<1(exercice), on a?⎷2-1<1et donc u

2=?⎷2-1-1<0.

Ainsi, il est impossible de définiru3. On a démontré :Fait 2 Il n"existe pas de suite(un)n,f-définie par récurrence, telle queu0= 2, où f:?R +//R x //⎷x-1.Suitesf-définies par récurrence4/12

b)Une solution p ossibleUne façon de régler une fois pour toutes cette question serait de supposer que la fonctionf:I-→R

stabilise son intervalle de définition,iede supposer que ?t?I, f(t)?I;

dit autrement, on aurait pu supposer dès le début qu"on considère une fonctionf:I-→I. En effet, dans

ce cas, siu0?Ialors, on au1, qui est égal àf(u0), est aussi dansI,etc.

Autrement dit, on aProposition 3

SoitIun intervalle deR, soitf:I-→I. Alors,

?a?I,?!(un)n?RN:? (un)n?RNestf-définie par récurrence u

0=a.Remarque

En fait, dans cette proposition, le fait queIest un intervalle ne joue aucune rôle. On peut le remplacer

par un ensembleDquelconque. Par exemple, on peut très bien considérer la fonction f:8 :R //R x //1 x .c)Retour au cas général

On choisit de ne pas faire cette hypothèse ici, car, généralement, la fonctionfvient plutôt définie sous la

formef:I-→R. À la place, on suppose que la suite(un)nest bien définie. 2.

Res trictionde fà des parties stables

SoitJ?Iun intervalle.

Rappelons qu"on dit queJest stable parfssiΔ

?t?J, f(t)?J.Proposition 4 Alors

Jest stable parf

u 0?J? =? ?n?N, un?J. Démonstration.--C"est très simple. On suppose queJest stable parfet queu0?J. Montrons le résultat par récurrence. •On note, pourk?N,P(k) :"uk?J». •Déjà,P(0), par hypothèse, est vraie. •Montrons que ?k?N,P(k) =?P(k+ 1). Soitk?Ntel queP(k)est vraie. Comme(un)nestf-définie par récurrence, onuk+1=f(uk). Or, uk?JetJest stable parf. Donc, on a bienf(uk)?J. D"où le résultat.

D"après le principe de récurrence, le résultat est démontré.Suitesf-définies par récurrence5/12

Remarques

Comme annoncé, la preuve est très simple. C"est ce qu"on appelle unerécurrence immédiate.

Très important :Il faudra s"entraîner dans l"étude des suitesf-définies par récurrence à éviter d"essayer de prouver

les résultats directement sur la suite mais à s"efforcer d"étudier d"abord la fonctionf. En effet,onestbeaucouppluspuissantpourétudierlafonctionfque pour étudier la suite(un)n: pour étudierf, on peut utiliser toute la puissance du calcul différentiel et dériverf; en traçant rapidement l"aspect deCf, on a beaucoup d"informations;

de même, le tableau des variations defdonne de façon synthétique beaucoup d"informations.En particulier, on en déduit le résultat suivant.

Corollaire 5

Soita?I. Alors, on a

?t?I, t>a=?f(t)>a? u

0>a=? ?n?N, un>a?

.On peut décliner et raffiner ce résulat. Par exemple

Corollaire 6

Soientb?Ietn0?N. Alors, on a

?t?I, t6b=?f(t)6b u n06b? =? ?n>n0, un6b.Corollaire 7

Soienta,b?Ietn0?N. Alors, on a

?t?I, a6t6b=?a6f(t)6b a6u06b? =? ?n?N, a6un6b.On retiendra :

Restreindrefà un intervalle stable permet

de restreindre le domaine de vie de(un)n.Exercice 8

Soit(un)n?RNla suite définie par

u 0>0 ?n?N, un+1=unun.

Montrer que?n?N?, un>1e

1/e.Suitesf-définies par récurrence6/12

V.T ransfertsde monotonie de fà(un)n

1.

Cas croissan t

Voici un principe très important :Quandfest croissante,(un)nest montone.Plus précisément, grâce au principe précédent de restriction du domaine de vie, on a : " là oùfest

croissante,(un)nest croissante ». Connaître les variations defest donc fondamental dans l"étude des

suitesf-récurrentes.Théorème 9

On supposefcroissante. Alors, on a

u

1>u0=?(un)ncroissante

etu16u0=?(un)ndécroissante.Ce théorème admet également une version " stricte » qu"on laisse au lecteur le soin d"énoncer.

Démonstration.--

•On supposeu1>u0. Comme annoncé, et comme précédemment, la preuve se fera par récurrence immédiate.

On note, pourn?N,P(n) :"un+1>un».

Déjà,P(0)est vraie par hypothèse.

Montrons que?n?N,P(n) =?P(n+ 1).

Soitn?Ntel queP(n)soit vraie. On a doncun6un+1. Or,fest croissante. Donc, on a f(un)6f(un+1)ieun+16un+2ieP(n+ 1). Ainsi, d"après le principe de récurrence, on a?n?N, un6un+1: la suite(un)nest croissante. •Si on au0>u1, on procède de même.

On retiendra :Sifest croissante, alors :

•la suite(un)nest monotone; le sens de variation de(un)nest déterminé par la position relative des deux premiers termes,u0etu1.Suitesf-définies par récurrence7/12

2.Cas décroissan t

Remarque

Dans ce paragraphe, on se place dans le cas oùf:I!I.a)Une astuce •La suite des termes pairs(u2n)n?Nvérifie u

2n+2=f(u2n+1) =f?

f(u2n)? = (f◦f)(u2n)pourn?N. •De même, la suite des termes impairs(u2n+1)n?Nvérifie u

2n+3=f(u2n+2) =f?

f(u2n+1)? = (f◦f)(u2n+1)pourn?N.

Autrement dit, on a prouvé :Proposition 10

Soitf:I-→Ret soit(un)n?RN.

Alors,

(un)nestf-définie par récurrence=?? (u2n)nest(f◦f)-définie par récurrence (u2n+1)nest(f◦f)-définie par récurrence.b)Application au cas décroissan t

Supposonsfdécroissante.Ce cas est plus subtil. En tout état de cause, il faut faire un dessin deCfet représenter les premiers

termes de(un)npour comprendre ce qui se passe : c"est le cas de " l"escargot ».x

IyRy=xC

fu 0u 1u 1u 2u 2u 3u 3u 4u 4u 5u 5u

6Pour analyser cette situation, on utilise l"astuce suivante :

fdécroissante=?f◦fcroissante.On peut donc appliquer les résultats du cas croissant aux suites(u2n)net(u2n+1)n.Suitesf-définies par récurrence8/12

Proposition 11

On supposefdécroissante. Alors, on a

u

2>u0=??

(u2n)ncroissante (u2n+1)ndécroissante etu26u0=?? (u2n)ndécroissante (u2n+1)ncroissante.Démonstration.-- •Supposons queu2>u0. On peut alors montrer par récurrence que?n?N, u2n+2>u2n. ~On note, pourn?N,P(n) :"u2n+2>u2n». ~Par hypothèse,P(0)est vraie.

~Montrons que?n?N,P(n) =?P(n+ 1).Soitn?Nest tel queu2n+2>u2n. Alors, en utilisant la croissance de la fonctionf◦f, on

obtient (f◦f)(u2n+2)>(f◦f)(u2n) ieu2n+4>u2n+2 ieP(n+ 1).

D"où le résultat :(u2n)nest croissante.Montrons maintenant que(u2n+1)nest décroissante.~Comme on au2>u0etfdécroissante, on af(u2)6f(u0)ieu3>u1.~On prouverait alors, par récurrence, que?n?N, u2n+36u2n+1.•Le casu26u0se traiterait de même.

c)

Un résultat utile

Rappelons un résultat classique qui peut être utile dans ce contexte.Proposition 12

Soit(vn)n?RNet soit??R. Alors, on a

u

2n-→?

u

2n+1-→??

=?un-→?.Démonstration.--On la laisse en exercice; il faut utiliser lesε >0.Suitesf-définies par récurrence9/12

VI.P ointsfixes de f

1.

P ointsfixes

On rappelle :

Définition 13

Soit??I. On dit que?est un point fixe defssiΔf(?) =?.Les points fixes defcorrespondent

aux points d"intersection entreCfet la droite(y=x).2.P ointsfixes de fet limites de(un)nThéorème 14

On supposefcontinue. Soit??I.

Alors, on a

u

n-→?=?f(?) =?.Démonstration.--On suppose queun-→?. On a donc, par propriété des suites extraites,un+1-→?.Or, comme on le verra plus tard dans le chapitre " Continuité », sifest continue, on af(un)-→f(?).

Donc, on aun+1-→f(?).

Par unicité de la limite d"une suite, on a doncf(?) =?.Remarque Attention, si` =2I, ce résultat n"a plus de sens et est faux.Exercice 15

Imaginer une fonctionf:R?+-→Rtelle que :

•fest continue; •fn"admet pas de limite en0+;

•il existe une suite(un)nf-définie par récurrence et vérifiantun-→0.Suitesf-définies par récurrence10/12

3.Un rés ultatd"infranc hissabilité

Proposition 16

On supposefcroissante. Soit??Iun point fixe def.

Alors, on a

u

06?=? ?n?N, un6?

etu0>?=? ?n?N, un>?.

Autrement dit, dans ce cas, les points fixes defsont infranchissables par(un)n.Démonstration.--Encore une fois, il s"agit de récurrences simples.

•On supposeu06?.

On note, pourn?N,P(n) :"un6?».

Déjà,P(0)est vraie par hypothèse.

Montrons que?n?N,P(n) =?P(n+ 1).

Soitn?Ntel queP(n)soit vraie. On a doncun6?. Or,fest croissante. Donc, on a f(un)6f(?)ieun+16?ieP(n+ 1). Ainsi, d"après le principe de récurrence, on a?n?N, un6?. •Si on au0>?, on procède de même. VII.

P ositionde Cfpar rapport à(y=x)Proposition 17

On a C fest au-dessus de(y=x)surI=?(un)nest croissante C

fest en-dessous de(y=x)surI=?(un)nest décroissante.Démonstration.--Cette fois-ci, ce ne sont pas des récurrences.

•On supposeCfest au-dessus de(y=x)surI. On a donc ?x?I, f(x)>x.Donc, comme?n?N, un?I, on a?n?N, f(un)>unie?n?N, un+1>un: la suite(un)nest bien croissante. •SiCfest en-dessous de(y=x)surI, on procède de même.

Suitesf-définies par récurrence11/12

VIII.Bilan

Voilà un plan possible pour étudier la suite(un)n. 1)

Rec herchedes p ointsfixes de f.

On résout l"équationf(?) =?, avec??I.

2)

Étude de f.

3)

Év entuellement,é tudede la p ositionrelativ ed eCfpar rapport à la droiteΔd"équationy=x.

Autrement dit, on étudie le signe de la fonctionx?-→f(x)-x. 4)

Restriction de fà un intervalle stable, dont généralement l"une des bornes est un point fixe def

5)Utilisation des résultats généraux énoncés ci-dessus, qui doivent être vus comme des réflexes et qui

doivent être redémontrés. IX.

E xercicesExercice 18

Étudier la suite(un)ndéfinie par

u 0= 1 ?n?N, un+1=⎷1 +un.Exercice 19

Étudier la suite(un)ndéfinie par

u 0= 1 ?n?N, un+1=⎷2 +un.Exercice 20

Étudier la suite(un)ndéfinie par

?u 0>1 ?n?N, un+1=13 u2n+23 .Exercice 21

Étudier la suite(un)ndéfinie par

?u 0=-2 ?n?N, un+1=un+1u n-1.Exercice 22

Étudier la suite(un)ndéfinie par

?u 0?? 0,12 ?n?N, un+1=un(1-un).Suitesf-définies par récurrence12/12quotesdbs_dbs31.pdfusesText_37

[PDF] f(x)=racine de x

[PDF] france métropolitaine 2016 maths corrigé

[PDF] x-ln(x^2+1) algorithme

[PDF] ce que jaurai aimé savoir avant de me marier pdf

[PDF] f(x)=1/x

[PDF] f x )= x 2 1

[PDF] f(x) = x^3

[PDF] f(x) calculer

[PDF] f(x)=2

[PDF] f(x)=x+1

[PDF] f'(x) dérivé

[PDF] f(x)=x^4

[PDF] f(x)=3

[PDF] livre mécanique appliquée pdf

[PDF] mécanique appliquée définition