 Chaînes de Markov
Chaînes de Markov
Résumé. Une chaîne de Markov est un processus aléatoire (Xn)n2N dont les transitions sont données par une matrice stochastique P(XnXn+1).
 Fiche résumée du cours de Processus de Markov par I.Kourkova 1
Fiche résumée du cours de Processus de Markov par I.Kourkova 1
Fiche résumée du cours de Processus de. Markov par I.Kourkova. 1 Chaînes de ii) i mène à j pour la chaîne de markov (Yn)n∈N. iii) Il existe i = i0
 CHAÎNES DE MARKOV
CHAÎNES DE MARKOV
Les résultats principaux de tout ce chapitre peuvent être résumés dans le théorème suivant : Théorème 29. Soit (Xn) une chaîne de Markov à ensemble d'états fini
 Modèles de Markov cachés
Modèles de Markov cachés
RÉSUMÉ . . . . . xi. INTRODUCTION. 1. CHAPITRE 1. THÉORIE ET INFÉRENCE SUR LES CHAÎNES l'étude est bel et bien u11e chaine de Markov de matrice de transition ...
 Modèles de chaînes de Markov cachées et de chaînes de Markov
Modèles de chaînes de Markov cachées et de chaînes de Markov
3 дек. 2018 г. Il ne reste plus qu'à itérer entre les étapes E et M jusqu'à convergence du vecteur. Ô. Pour résumer l'algorithme EM se construit en deux étapes ...
 Les techniques Monte Carlo par chaînes de Markov appliquées à la
Les techniques Monte Carlo par chaînes de Markov appliquées à la
26 мар. 2018 г. En résumé les équations d'évolution des densités de quarks non singulets sont : ... approche basée sur les méthodes Monte Carlo par chaînes de ...
 Chaînes de Markov.
Chaînes de Markov.
Alors conditionnellement à Xn = x le processus. Xn+ est une chaîne de Markov de matrice de transition P
 Tricks espérance/conditionnelle
Tricks espérance/conditionnelle
0.5 Chaînes de Markov. Quelques notations: (Qf)(x) = ∑ y∈E. Q(x y)f(y). (µQ)(x) = ∑ y∈E. µ(y)Q(y
 Chaînes de Markov cachées à bruit généralisé
Chaînes de Markov cachées à bruit généralisé
17 июн. 2022 г. Résumé – Les chaînes de Markov cachées sont des modèles très populaires pour le traitement non-supervisé du signal dans un contexte bayésien ...
 Chaînes de Markov
Chaînes de Markov
Résumé. Une chaîne de Markov est un processus aléatoire (Xn)n2N dont les transitions sont données par une matrice stochastique P(XnXn+1).
 Fiche résumée du cours de Processus de Markov par I.Kourkova 1
Fiche résumée du cours de Processus de Markov par I.Kourkova 1
1 Chaînes de Markov à temps continu sur un espace dénombrable. 1.1 loi exponentielle. Définition 1.1.1 (Loi exponentielle) Une variable aléatoire T suit une.
 CHAÎNES DE MARKOV
CHAÎNES DE MARKOV
Soit Xn est une chaîne de Markov de matrice de transition P et soit ?0 la loi de X0. tout ce chapitre peuvent être résumés dans le théorème suivant :.
 Chaînes de Markov.
Chaînes de Markov.
Alors conditionnellement à Xn = x le processus. Xn+ est une chaîne de Markov de matrice de transition P
 IFT-3655 Modèles Stochastiques orange Chaînes de Markov en
IFT-3655 Modèles Stochastiques orange Chaînes de Markov en
Chaˆ?ne de Markov en temps discret. On consid`ere un processus stochastique en temps discret {Xn n = 0
 Modèles stochastiques Chaîne de Markov en temps continu
Modèles stochastiques Chaîne de Markov en temps continu
Dans le chapître précédent sur les chaînes de Markov les moments (temps) Le processus stochastique est alors u chaîne de Markov en temps co.
 6 Chaînes de Markov - Etude dune classe particulière de processus
6 Chaînes de Markov - Etude dune classe particulière de processus
aléatoires : chaînes de Markov d'ordre1. 2. généralisation : chaîne d'ordre supérieur. 3. chaines de Markov non-homogène dans le temps. 4.
 Introduction aux chaînes de Markov
Introduction aux chaînes de Markov
? Exercice 71. Soit (Xn)n?N une cha?ne de Markov homog`ene de matrice de transition Q et de loi initiale µ. On.
 Chaînes de Markov (et applications)
Chaînes de Markov (et applications)
22 Feb 2021 Les coefficients d'une matrice stochastique sont dans [0 1]. Proposition 1. Si Q est la matrice de transition d'une chaîne de Markov
 Chaînes de Markov et martingales
Chaînes de Markov et martingales
Définition 5.6 Soit E un espace vectoriel réel et X une partie de E. L'en- veloppe convexe de X notée cv(x) est l'ensemble des points combinaisons linéaires d'
 [PDF] CHAÎNES DE MARKOV - Institut de Mathématiques de Bordeaux
[PDF] CHAÎNES DE MARKOV - Institut de Mathématiques de Bordeaux
Les résultats principaux de tout ce chapitre peuvent être résumés dans le théorème suivant : Théorème 29 Soit (Xn) une chaîne de Markov à ensemble d'états fini
 [PDF] Chaînes de Markov
[PDF] Chaînes de Markov
Résumé Une chaîne de Markov est un processus aléatoire (Xn)n2N dont les transitions sont données par une matrice stochastique P(XnXn+1)
 [PDF] CHAÎNES DE MARKOV - ceremade
[PDF] CHAÎNES DE MARKOV - ceremade
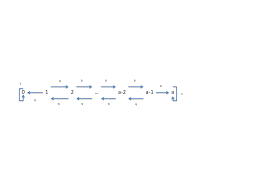
5 3 4 Graphe associé à une chaîne de Markov homogène recherche se situent dans le domaine de la théorie des nombres et en analyse ses recherches
 [PDF] Chaînes de Markov - Institut Camille Jordan
[PDF] Chaînes de Markov - Institut Camille Jordan
est appelée une chaîne de Markov d'espace d'états S lorsqu'il existe une famille de noyaux de transitions (pn(··))n?0 sur S et une loi de probabilité ?
 [PDF] Chapitre 8 Chaˆ?nes de Markov - DI ENS
[PDF] Chapitre 8 Chaˆ?nes de Markov - DI ENS
En fait les cha?nes de Markov sont des processus stochastiques dont l'évolution est régie par une équation de récurrence du type Xn+1 = f(XnZn+1) o`u {Zn}n?
 [PDF] Chaînes de Markov (et applications)
[PDF] Chaînes de Markov (et applications)
22 fév 2021 · Xn est donc bien une chaîne de Markov homogène avec matrice de transition Q Exercice 4 Introduisons un facteur de fatigue f ? (0 1) et
 [PDF] Fiche résumée du cours de Processus de Markov par IKourkova 1
[PDF] Fiche résumée du cours de Processus de Markov par IKourkova 1
Fiche résumée du cours de Processus de Markov par I Kourkova 1 Chaînes de Markov à temps continu sur un espace dénombrable 1 1 loi exponentielle
 [PDF] Introduction aux chaines de Markov - CERMICS
[PDF] Introduction aux chaines de Markov - CERMICS
Soit P une matrice stochastique sur E Une suite de variables aléatoires (Xnn ? N) `a valeurs dans E est appelée cha?ne de Markov de matrice de transition P
 [PDF] Chaînes de Markov et martingales - Index of /
[PDF] Chaînes de Markov et martingales - Index of /
Définition 5 6 Soit E un espace vectoriel réel et X une partie de E L'en- veloppe convexe de X notée cv(x) est l'ensemble des points combinaisons linéaires d'
 [PDF] Chaînes de Markov - arthur charpentier
[PDF] Chaînes de Markov - arthur charpentier
École Nationale de la Statistique et d'Analyse de l'Information En 1907 Ehrenfest a introduit des chaînes de Markov pour étudier la diffusion d'un gaz
Chaînes de Markov et martingales
Pierron Théo
ENS Ker Lann
2Table des matières
1 Conditionnement1
1.1 Un exemple. . . . . . . . . . . . . . . . . . . . . . . . . . . . 1
1.2 Espérance conditionnelle - Définition. . . . . . . . . . . . . . 2
1.3 Espérance conditionnelle - Propriétés. . . . . . . . . . . . . . 3
1.3.1 Premières propriétés. . . . . . . . . . . . . . . . . . . 3
1.3.2 Extensions des théorèmes usuels. . . . . . . . . . . . . 4
1.3.3 Propriétés spécifiques. . . . . . . . . . . . . . . . . . . 5
1.4 Calcul d"espérance conditionnelle. . . . . . . . . . . . . . . . 6
1.4.1 Cas des variables discrètes. . . . . . . . . . . . . . . . 6
1.4.2 Cas des variables à densité. . . . . . . . . . . . . . . . 7
1.4.3 Variables gaussiennes. . . . . . . . . . . . . . . . . . . 7
1.5 Notion de loi conditionnelle. . . . . . . . . . . . . . . . . . . 8
1.5.1 Définitions. . . . . . . . . . . . . . . . . . . . . . . . . 8
1.5.2 Existence et unicité. . . . . . . . . . . . . . . . . . . . 9
1.5.3 En pratique. . . . . . . . . . . . . . . . . . . . . . . . 9
2 Martingales et temps d"arrêt11
2.1 Définitions et exemples. . . . . . . . . . . . . . . . . . . . . . 11
2.1.1 Transformées de martingales. . . . . . . . . . . . . . . 12
2.2 Temps d"arrêt est théorèmes. . . . . . . . . . . . . . . . . . . 13
2.2.1 Notion de temps d"arrêt. . . . . . . . . . . . . . . . . 13
2.2.2 Théorème d"arrêt. . . . . . . . . . . . . . . . . . . . . 14
2.3 Théorème d"arrêt. . . . . . . . . . . . . . . . . . . . . . . . . 15
3 Convergence de martingales17
3.1 Convergence presque sûre. . . . . . . . . . . . . . . . . . . . 17
3.1.1 Le cas positif. . . . . . . . . . . . . . . . . . . . . . . 17
3.1.2 Cas borné dansL1. . . . . . . . . . . . . . . . . . . . 18
3.2 Convergence dansL1. . . . . . . . . . . . . . . . . . . . . . . 20
3.2.1 Martingales fermées. . . . . . . . . . . . . . . . . . . . 20
3.2.2 Uniforme intégrabilité. . . . . . . . . . . . . . . . . . 21
i iiTABLE DES MATIÈRES3.3 ConvergenceLpavecp >1. . . . . . . . . . . . . . . . . . . . 23
3.3.1 Inégalités maximales et convergenceLp. . . . . . . . . 23
3.3.2 Cas des martingale de carré intégrable. . . . . . . . . 25
3.3.3 Décomposition de Doob(-Meyer). . . . . . . . . . . . . 26
3.3.4 Théorème classiques pour les martingales. . . . . . . . 27
3.4 Martingales rétrogrades. . . . . . . . . . . . . . . . . . . . . . 28
4 Application des martingales31
4.1 Galton-Watson. . . . . . . . . . . . . . . . . . . . . . . . . . 31
4.2 Wright-Fisher. . . . . . . . . . . . . . . . . . . . . . . . . . . 33
4.3 Inégalité d"Azuma. . . . . . . . . . . . . . . . . . . . . . . . . 33
5 Chaînes de Markov35
5.1 Probabilités de transition et matrices. . . . . . . . . . . . . . 35
5.1.1 Premières propriétés. . . . . . . . . . . . . . . . . . . 36
5.1.2 Exemples. . . . . . . . . . . . . . . . . . . . . . . . . 38
5.2 Un peu d"algèbre et de géométrie. . . . . . . . . . . . . . . . 38
5.2.1 Théorème de Perron-Frobénius. . . . . . . . . . . . . 38
5.2.2 Matrices bistochastiques. . . . . . . . . . . . . . . . . 40
5.3 Propriété de Markov. . . . . . . . . . . . . . . . . . . . . . . 41
5.3.1 Chaîne de Markov canonique. . . . . . . . . . . . . . 41
5.3.2 Propriété de Markov. . . . . . . . . . . . . . . . . . . 43
5.4 Applications de la propriété de Markov. . . . . . . . . . . . . 45
6 Classification des états47
6.1 Dichotomie récurrence/transcience. . . . . . . . . . . . . . . 47
6.1.1 Motivations. . . . . . . . . . . . . . . . . . . . . . . . 47
6.1.2 États récurrents et transcients. . . . . . . . . . . . . . 48
6.1.3 Absorption dans les classes de récurrence. . . . . . . . 52
6.2 Mesure invariante. . . . . . . . . . . . . . . . . . . . . . . . . 54
6.2.1 Définitions et exemples. . . . . . . . . . . . . . . . . . 54
6.2.2 Mesure invariante et récurrence. . . . . . . . . . . . . 56
7 Comportement asymptotique59
7.1 Convergence à l"équilibre. . . . . . . . . . . . . . . . . . . . . 59
7.1.1 CasEfini. . . . . . . . . . . . . . . . . . . . . . . . . 59
7.1.2 Le cas général. . . . . . . . . . . . . . . . . . . . . . . 59
7.2 Théorème ergodique. . . . . . . . . . . . . . . . . . . . . . . 61
Chapitre 1Conditionnement1.1 Un exemple
Soient (Ω,F,P) un espace de probabilité etX: Ω→ {x1,...,xm},Y: Ω→ {y1,...,yn}deux variables aléatoires discrètes.La formule :
?F→[0,1]A?→P(A|Y=yj) =P(A∩{Y=yj})
P(Y=yj)
définit une nouvelle probabilité sur (Ω,F), notéePY=yj.Définition 1.1
L"espérance conditionnelle deXsachant queY=yjest l"espérance deXsous la loiPY=yj.E(X|Y=yj) =m?
i=0x iP(X=xi|Y=yj) =ujDéfinition 1.2
L"espérance conditionnelle deXsachantYest la variable aléatoire :U(ω)?→ujsiY(ω) =yj
Exemple 1.1Ω =?1,6?,F=P(Ω) etPuniforme.
Si on prendX= Id etY= 1{2,4,6}, on a :
U(ω) =E(X|Y)(ω) =???4 siωest pair
3 sinon
NotonsG=σ(Y). Elle est formée des unions d"atomesGj={Y=yj}.Uest constante sur chacun desGj, doncG-mesurable.
1CHAPITRE 1. CONDITIONNEMENT
Par ailleurs,
E(U1Gj) =ujP(Gj) =n?
i=1x iP(X=xi|Y=yj)P(Y=yj) n? i=1x iP(X=xietY=yj) =E(X1Gj)Pour toutG? G,E(U1G) =E(X1G).
1.2 Espérance conditionnelle - Définition
Par la suite, on fixe un espace de probabilité (Ω,F,P).Théorème 1.1
SoientGune sous-tribu deFetX?L1(Ω,F,P). Il existe une unique variableE(X| G)?L1(Ω,G,P)qui vérifie : ?G? G,E(E(X|G)1G) =E(X1G)Remarque 1.1
Cette dernière propriété est équivalente à : pour toute variable aléatoireZG-mesurable bornée,E(E(X| G)Z) =E(XZ).
De plus, siX?0p.s.,E(X|G)?0p.s.
L"unicité est dansL1!
E(X| G)estG-mesurable.
Démonstration.
! : SoientYetY?deux versions deE(X| G).AlorsYetY?sontG-mesurables doncG={Y > Y?} ? G.
On a aussiE(Y1G) =E(Y?1G), doncE((Y-Y?)1Y-Y?>0) = 0 etY?Y? p.s.Par symétrie,Y=Y?.
?: Dans le cas oùX?L2(Ω,F,P). Cet espace est un espace de Hilbert dontL2(Ω,G,P) est un sev complet.SoitYla projection orthogonale deX. On a :
?E((Y-X)2) = infZ?L2(Ω,G,P)E((X-Z)2) ?Z?L2(Ω,},P),E((X-Y)Z) = 0La variable aléatoireYconvient.
Passage deL2àL1
Lemme 1.1.1 De positivité
SoitUune variable aléatoire positive bornée. AlorsE(U| G)?0 p.s.PierronThéoPage 2 Tous droits réservés
1.3. ESPÉRANCE CONDITIONNELLE - PROPRIÉTÉS
Démonstration.SoitWune version deE(U| G).
Par l"absurde, siP(W <0)>0 alors?n?Ntel queP?
W?-1 n? G>0.On a alors
0?E(U1G) =E(W1G)?-1
nP(G)<0Contradiction. DoncP(W?0) = 1.
SiX?L1, il est loisible de supposerX?0 p.s.et il existe une suite croissante de variables aléatoiresXnbornées (donc dansL2) qui converge versXsansL1. Alors si on poseYn=E(Xn| G), on aYn croissante positive (lemme1.1.1)
On poseY= limsup
n→+∞Yn.YestG-mesurable et par convergence mono- tone, pour toutG? G,E(Xn1G) =E(Yn1G). En passant à la limite,E(X1G) =E(Y1G).
Exemple 1.2Soit (Ω,F,P) = (]0,1[,B(]0,1[),λ).Soitf?L1(Ω,F,P) etG=σ(]i-1
n,in],i??1,n?).E(f| G) =n?
i=1f i1]i-1 n,in] avecfi=n? i n i-1 nfdλ.E(f| G) est bienG-mesurable et par ailleurs,
E(f1]j-1
n,jn]) =E? n? i=1f i1]i-1n,in]1]j-1n,jn]? =E(fj1]j-1 n,jn])Théorème 1.2
SiXest un variable aléatoire positive alors la formule E(X| G) = limn→+∞E(X?n| G)définit une variableG-mesurable caractérisée par : ?Z?0G-mesurable,E(XZ) =E(E(X| G)Z)1.3 Espérance conditionnelle - Propriétés
1.3.1 Premières propriétés
Proposition 1.1SoitX?L1(Ω,F,P) etGune sous-tribu deF.PierronThéoPage 3 Tous droits réservés
CHAPITRE 1. CONDITIONNEMENT
1. SiXestG-mesurable alorsE(X| G) =Xp.s.
2.X?→E(X| G) est linéaire
3.E(E(X| G)) =E(X)
4.|E(X| G)|?E(|X| | G) p.s.
5. SiX?X?p.s.,E(X| G)?E(X?| G) p.s.
Démonstration.
1. Unicité
2. SiU=E(X| G) etV=E(Y| G), alorsαU+βVest une version de
E(αX+βY| G).
3. Définition avec 1
G= 1Ω= 1.
4.|E(X| G)|=|E(X+| G)-E(X-| G)|?E(X+| G) +E(X-| G) =
E(|X| | G).
5. Linéarité+lemme
1.1.1Remarque 1.2
?E(X| G)?1??X?1.
Plus clairement, l"opérateurX?→E(X| G)linéaire positif de norme1.1.3.2 Extensions des théorèmes usuels
Proposition 1.2SoitX?L1(Ω,F,P),Gune sous-tribu deF.1. Si (Xn)nest une suite positive croissante qui tend versXp.s. alors
E(Xn| G) croît versE(X| G) p.s.
2. Si (Xn)nest une suite positive,E(liminfXn| G)?liminfE(Xn| G)
p.s.3. Si|Xn(ω)|?V(ω) avecE(V)<∞et siXnconverge p.s. versXalors
E(Xn| G) converge p.s. versE(X| G).
4. Sic:R→Rest convexe etE(|c(X)|)<∞, alorsE(c(X)| G)?
c(E(X| G)) p.s.Démonstration.
1. Voir passageL2→L1.
2. Exo
3. Exo
PierronThéoPage 4 Tous droits réservés
1.3. ESPÉRANCE CONDITIONNELLE - PROPRIÉTÉS
4. On utilisec(x) = supn?N(anx+bn). Soitn?N.
On ac(X)?anX+bndoncE(c(X)| G)?anE(X| G) +bnp.s.
Comme on a un sup sur un ensemble dénombrable, on peut passer au sup et on a :E(c(X)| G)?c(E(X| G))p.s.
Remarque 1.3 On a ainsi, pour toutp?1,?E(X| G)?p??X?p.1.3.3 Propriétés spécifiques
Proposition 1.3SoientXune variable aléatoire etYune variableG- mesurable.E(XY| G) =YE(X| G) p.s.
dès lors que les espérances sont bien définie. Démonstration.YE(X| G) estG-mesurable comme produit de deux va- riablesG-mesurables.SiG? G, on a
E(YE(X| G)1G) =E(Y1GE(X| G)) =E(XY1G)
Par unicité de l"espérance conditionnelle, on a le résultat. Proposition 1.4SoientH ? G ? Fdeux sous-tribus etX?L1(Ω,F,P). AlorsE(E(X| G)| H) =E(X| H) p.s.
Démonstration.E(E(X| G)| H) estH-mesurable. SoitH? H.E(E(E(X| G)| H)1H) =E(E(E(X1H| G)| H)) =E(X1H)
Proposition 1.5Deux tribusGetHsont indépendantes ssi pour toutG? G,E(1G| H) =E(1G) =P(G) p.s.
Remarque 1.4XetYsont indépendantes ssi pour toutgmesurablesE(g(X)|Y) =E(g(X))p.s.
Démonstration.
?SiH? HetG? G. On aE(1G1H) =E(1G)E(1H) =E(E(1G)1H)
doncE(1G) =E(1G| H) par unicité.PierronThéoPage 5 Tous droits réservés
CHAPITRE 1. CONDITIONNEMENT
?SiH? HetG? G, on aP(H∩G) =E(1H1G) =E(E(1G)1H) =P(G)P(H)
d"oùH??G. Proposition 1.6SoientX,Ydeux variables aléatoires à valeurs dansE,F, Gune sous-tribu deF. On suppose queX?? Get queYestG-mesurable.Alors pour toutf:E×F→Rmesurable,
E(f(X,Y)| G) =?
E f(x,Y)PX(dx) = Φ(Y) Démonstration.Φ(Y) estG-mesurable. SoitZG-mesurable bornée, on a :E(f(X,Y)Z) =?
f(x,y)zP(X,Y,Z)(dx,dy,dz) f(x,y)PX(dx)zPY,Z(dy,dz) =E(Φ(Y)Z)1.4 Calcul d"espérance conditionnelle
1.4.1 Cas des variables discrètes
SoitX?L1(Ω,F,P) etY: Ω→ {y1,...,yn}une variable discrète.E(X|Y) =E(X|σ(Y))
σ(Y) est engendrée par les atomesGi={Y=yi}.
Proposition 1.7On a
E(X|Y) =∞?
i=1E(X1Gi)P(Gi)1Gi
Démonstration.Le membre de droite estσ(Y)-mesurable. De plus, on a E i=1E(X1Gi)P(Gi)1Gi1Gj?
=E(X1Gj)PierronThéoPage 6 Tous droits réservés
1.4. CALCUL D"ESPÉRANCE CONDITIONNELLE
1.4.2 Cas des variables à densité
Proposition 1.8Soit (X,Y) de densitép(x,y) par rapport à la mesure deLebesgue. Alors pour tout fonction mesurableh,
E(h(X)|Y) =?(Y)
avec ?(u) =?????? h(x)p(x,u)dx ?ρ(x,u)dxsip(x,u)dx >00 sinon
(densité conditionnelle deXpar rapport àY).Démonstration.?(Y) estY-mesurable.
Soitgmesurable bornée.
E(h(x)g(y)) =?
h(x)g(y)p(x,y)dxdyquotesdbs_dbs7.pdfusesText_13[PDF] chaine d'acquisition de données
[PDF] chaine de mesure audioprothèse
[PDF] acquisition de données du capteur ? l ordinateur
[PDF] chaine de mesure pdf
[PDF] chaine d'acquisition capteur
[PDF] les capteurs exercices corrigés
[PDF] chaine de markov apériodique
[PDF] chaine de markov apériodique exemple
[PDF] chaine de markov reversible
[PDF] chaine de markov récurrente
[PDF] chaine de markov exemple
[PDF] chaine de markov irreductible exemple
[PDF] chaine de markov exercice corrigé
[PDF] chaine énergétique barrage hydraulique
