[PDF] IFT-3655 Modèles Stochastiques orange Chaînes de Markov en

View - Download IFT-3655 Modèles Stochastiques orange Chaînes de Markov en

Previous PDF

Next PDF

Draft1

IFT-3655, Modeles Stochastiques

Cha^nes de Markov en temps discret

Prof. Pierre L'Ecuyer

DIRO, Universite de Montreal

Ces \diapos" sont surtout un support pour les presentations en classe. Elles ne contiennent pas toutes les explications detaillees. Pour cela il est recommande d'etudier le livre recommande, de Sheldon Ross.

Draft2

Cha^ne de Markov en temps discret

On considere un processus stochastique en

temps discret fXn;n= 0;1;2;:::gdont l'espace d'etatsX(l'ensemble de tous les etats possibles) est denombrable. On va habituellement numeroter les etats par des entiers non negatifs, et ainsi supposer queX=f0;1;:::;rg (ni) ouX=f0;1;2;:::g(inni).Ce processus est unec ha^nede Ma rkovhomog enesi P[Xn+1=jjXn=i;Xn1=in1;:::;X1=i1;X0=i0] =P[Xn+1=jjXn=i] =Pi;j: En d'autres mots, la loi de probabilite du prochain etatXn+1conditionnellement a

l'histoire passee ne depend que de l'etat actuelXnet ne depend pas den.LesPi;jsont lesp robabilitesde tran sitionde la cha ^ne.

L'adjectif

homog ene veut dire que ces p robabilitesn ed ependentpas de n.

Draft3

LesPi;jdoivent necessairement satisfaire:

P i;j0 for alli;j;1X j=1P i;j= 1 for alli:

Ils sont les elements de la

matrice de transition P=0 B BB@P

0;0P0;1P0;2

P

1;0P1;1P1;2

P

2;0P2;1P2;2

.........1 C CCA

Draft4

Exemple.Deux etats possibles: \il pleut" (0) et \il ne pleut pas" (1). Le temps est en jours. =P[pluie demainjpluie aujourd'hui],=P[pluie demainjpas de pluie aujourd'hui]. On a P=1

1Exemple.Marche aleatoiresur les entiers:

P i;i+1=p= 1Pi;i1;pouri2Z:Modele de parieur: Comme ci-haut maisP0;0=PN;N= 1 pour unN>0. X nrepresente la fortune du joueur a l'etapen. QuandXn= 0, il est ruine; quandXn=N, il s'arr^ete de jouer.

Draft5

Risque d'assurance d'un client: modele Bonus-Malus Dans ce modele,Xnrepresente le risque d'un client pour une cie d'assurance, en fonction de son historique d'accidents. L'idee est de denir un nombre ni de cat egoriesde risque , et une cha^ne de Markov dont les etats sont ces categories. Un client dans l'etatiqui akaccidents durant l'annee passera a l'etatsi(k), ou lessi(k) sont species a l'avance. Par exemple, on pourrait avoirsi(k) =i+kI[k= 0] , ou bien s

i(k) =i+ 2kI[k= 0], ou une fonction plus complexe.On suppose que le nombreYd'accidents par un client durant une annee estPoisson(), ou

le parametre=cpeut dependre du client et ^etre inconnu. Si le client est dans l'etati, il auraY=kaccidents avec probabiliteek=k!, et sa probabilite de passer a l'etatjest P i;j=X fk:si(k)=jge k=k! Il y a dierentes facons d'utiliser ce modele. Idealement, on voudrait pouvoir \apprendre"c et la loi des montants de reclamations, pour chaque client, en fonction de son historique.

Draft6

Equation de Chapman-Kolmogorov

Soit P(n) i;j=P[Xn=jjX0=i]; la probabilite de passer deiajen exactementnetapes.Equation de Chapman-Kolmogorov: P (n+m) i;j=1X k=0P[Xn+m=jjXn=k]P[Xn=kjX0=i] =1X k=0P(n) i;kP(m) k;j En notation matricielle, siP(n)est la matrice contenant lesP(n) i;j, cela donne P (n+m)=P(n)P(m): En particulier,P(2)=PP, et par induction surn, on aP(n)=P(n1)P=Pn. Similaire aux matrices donnant les nombres de chemins de longueurnentre chaque paire de sommets dans un graphe.

Draft7

Exemple.Dans l'exemple de \pluie" vs \non pluie", supposons que= 0:7 et= 0:4, de sorte que P=1 1 =0:7 0:3

0:4 0:6

les probabilites de transition en deux jours et en 4 jours sont: P

2=0:61 0:39

0:52 0:48

;P4=0:5749 0:4251

0:5668 0:4332

Que se passe-t-il avecPnquandn! 1?On a

lim n!1Pn=4=7 3=7

4=7 3=7

Les lignes sont identiques et donnent les

p robabiliteslimites des deux etats.

Interpretation.

Draft8

Exemple.On dispose de balles rouges et de balles bleues, et d'une urne qui contient 2 balles.A chaque etape, on tire une balle de l'urne et on la remplace par une balle de la m^eme couleur avec probabilite 0.8 et de l'autre couleur avec probabilite 0.2. On denit une cha^ne ouXnest lenomb rede balles rouges dans l'ur ne al' etapen. L'espace d'etats est f0;1;2get la matrice des probabilites de transition est P=0 @0:8 0:2 0

0:1 0:8 0:1

0 0:2 0:81

A SiX0= 2 (2 balles rouges au depart), alors lap remiereballe tir eeest certainement rouge. Soitbnla probabilite que la (n+ 1)-ieme balle tiree est rouge. On aura b n= 1P[Xn= 2jX0= 2] + (1=2)P[Xn= 1jX0= 2] =P(n)

2;2+P(n)

2;1=2:Par exemple, en calculantP4et on trouveP(4)

2;2= 0:4872 etP(4)

2;1= 0:4352, ce qui donne

b

4= 0:4872 + 0:4352=2 = 0:7048.Que se passe-t-ilquand n! 1? On peut montrer quePnconverge vers une matrice dont

les 3 lignes sont (1=4;1=2;1=4), et quebn!1=2, ce qui correspond a l'intuition.

Draft9

Exemple 4.11 du livre: Encore le probleme du collectionneur de capsules. Il y aktypes de capsules.A chaque etape on tire une capsule, avecp robabilite1 =kpour chaque type. SoitXnle nombre de types que l'on a apresntirages. Les probabilites de transition sontP0;1= 1,Pk;k= 1, P i;i=i=k= 1Pi;i+1pouriPest une matrice (k+ 1)(k+ 1). La probabilite d'avoir exactementjtypes apresntirages estP(n) 0;j. La probabilite d'avoir une collection complete apresntirages estP(n)

0;k.Et si les probabilites ne sontpas toutes 1 =k?Le modele aveck+ 1 etats ne tient plus.

L'etat doit indiquer quelles capsules il nous manque! Donc 2 ketats possibles.Et si on veut \apprendre" ces probabilites a partir d'observations?

Draft10

Cha^nes avec etats absorbants ou tabousParfois, pour une cha^ne de Markov, on a un sous-ensemble d'etatsA X et on s'interesse a

un evenement qui depend deN= inffn1 :Xn2 Ag, l'instant de la premiere visite aA, ou

du premier retour aAsi on y est deja. SiXnn'atteint jamaisA, on aN=1.On peut vouloir calculer par exemple

=P[NmjX0=i]: Dans ce genre de situation, on peut reduire la taille de la cha^ne en fusionnant tous les etats deAen un seul etat absorbant, disons . Quand la cha^ne atteint cet etat, elle y reste.

La nouvelle cha^nefWn;n0gest denie par

W n=XnpournOn obtient=P[NmjX0=i] =P[Wm= jW0=i] =Q(m) i;.

Draft11

Exemple:On tire a pile ou face et on s'interesse a laloi de p robabilitede N, le nombre de tirages requis pour avoirsfaces d'alee. SoitXnle nombre de faces de suite que l'on vient d'obtenir rendu a l'etapensi on a face a cette etape, etXn= 0 si on a pile.

On pose ensuiteA=fsg, = s, etN= inffn1 :Xn2 Ag.

AinsiWn=Xnavant d'avoir atteints, et par la suiteWn=s= (le cimetiere).Par exemple, pours= 3, lesQi;jsont donnes par

Q=0 B

B@1=2 1=2 0 0

1=2 0 1=2 0

1=2 0 0 1=2

0 0 0 11

C CA:

Pour chaquen>0, l'elementQ(n)

0;sde la matriceQndonne la valeur deP(Nn).

On peut ainsi calculer toute la distribution deN.

Draft12

Contraintes sur les trajectoires

Sii;j62 A, la probabilite queXm=jet que la cha^ne n'ait pas visite l'ensembleAjusqu'a l'etapems'ecrit =P[Xm=j;N>m1jX0=i]: Pour calculer, il sut de construireQet la cha^nefWn;n0gcomme ci-haut.

L'elementQ(m)

i;jdonne la probabilitecherchee.Pour le cas ouj2 A, voir Ross (2014), page 193.

Draft13

Classication des etats

On dit qu'un etatjestacces siblede l' etatis'il existe unn0 tel quep(n) ij>0. Cela veut dire que si on est dans l'etati, la probabilite d'atteindrejeventuellement n'est pas nulle.

Notez queiest toujours accessible dei.

Deux etatsietjcommuniquentsi chacun est acce ssiblede l'autre. On note cela i$j.

La communication est une

relation d' equivalence : c'est re exif et symetrique (decoule directement de la denition), et aussi transitif (decoule de l'equation de

Chapman-Kolmogorov).

Les classes d'equivalence forment une

pa rtition de l'espace d' etatsX.

On les appelle les

classes de communication

La cha^ne est

irreductible

si tous les etatscommuniquent (une se uleclasse d' equivalence).On peut representer une cha^ne de Markov a espace d'etats discret par un graphe oriente.

Les etats sont les

sommets , les transitions de probabilite positive sont les a rcs , et on peut aller deiajennetapes s'il y a un chemin deiajde longueurn.

Draft14

Exemple.

P=0 @1=2 1=2 0

1=2 1=4 1=4

0 1=3 2=31

A0121/2

1/21/4

1/31/21/42/3

Ici, tous les etats communiquent. La cha^ne est irreductible.

Exemple.

P=0 B

B@1=2 1=2 0 0

1=2 1=2 0 0

1=4 1=4 1=4 1=4

0 0 0 11

C

CA:01231/21/21/41

1/2 1/2

1/41/41/4

Ici, on a trois classes:f0;1g,f2g, etf3g. L'etat 2 esttransitoire et l' etat3 est abso rbant.

Draft15

Etats recurrents et transitoires

Pour chaque etati, soitfila probabilite que si on part dei, on va y revenir ulterieurement. L'etatiest ditr ecurrentsi fi= 1 (on est certain d'y revenir) ettransitoire si fi<1.

Voir les exemples.Sifi= 1, le processus va revenir aiavec probabilite 1, puis va y revenir encore une fois avec

probabilite 1, et ainsi de suite. La cha^ne va donc revenir aiune innite de fois, et le nombre espere de visites aiest necessairement inni.

Par contre,

si fi<1, a chaque passage ai, la cha^ne va y revenir avec probabilitefi<1, et n'y reviendra plus jamais avec probabilite 1fi. Le nombre de retours aiest donc dans ce cas une v.a. geometrique de parametrep= 1fi, dont l'esperance est (1p)=p<1 (ici, chaque retour correspond a un \echec"). Donc sifi<1, le nombre de visites a l'etatiest ni avec probabilite 1, et le nombre espere de visites aiest ni.

Draft16

SoitMi=P1

n=1I[Xn=i] le nombre de retours a l'etati, en supposant queX0=i.

On afi= 1 ssiE[MijX0=i] =1. Mais

E[MijX0=i] =1X

n=1E[I(Xn=i)jX0=i] =1X n=1P[Xn=ijX0=i] =1X n=1P(n) i;i:Proposition.Un etatiestr ecurrentsi P1 n=1P(n)

i;i=1ettransitoire sinon. Corollaire.Le caractere recurrent ou transitoire est une propriete de classe: siiest recurrent

[transitoire] eti$j, alorsjest recurrent [transitoire].

Preuve

: Prenonsmetktels queP(m) j;i>0 etP(k) i;j>0, i.e.,i$j. Siiest recurrent, 1 X n=1P(n) j;j1X n=1P(m+n+k) j;j1X n=1P(m) j;iP(n) i;iP(k) i;jP(m) j;iP(k) i;j1 X n=1P(n) i;i=1:

Draft17

Exemple

P=0 B

BBB@1=2 1=2 0 0 0

1=2 1=2 0 0 0

0 0 1=2 1=2 0

0 0 1=2 1=2 0

1=4 1=4 0 0 1=21

C CCCA:

Quelles sont les classes de communication, et lesquelles sont recurrentes?Il y a trois classes:f0;1g,f2;3g, etf4g.

Les deux premieres sont

r ecurrentes et la troisi emeest transitoire

Rendu ici, 23 janv. 2020

Draft18

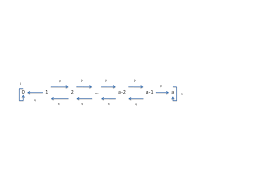
Une marche aleatoire sur les entiers-2-10123p

1pp 1pp 1pp 1pp

1pIci, tous les etats communiquent (une seule classe), donc ils sont ou bien tous recurrents, ou

bien tous transitoires! Pour savoir s'ils sont recurrents ou pas, on va calculer

E[M0jX0= 0] =1X

n=1P(n) 0;0:

Draft19

On sait qu'on ne peut revenir a 0 qu'en un nombre pair de coups, donc il sut de considerer les termes de la formeP(2n)

0;0, i.e., allernfois a gauche etnfois a droite:

P (2n)

0;0=2n

n p n(1p)n=(2n)!n!n!(p(1p))n

p4n(2n=e)2n2n(n=e)2n(p(1p))n=(4p(1p))npnen utilisant l'approximation de Stirlingn!p2n(n=e)n.Donc les etats sont recurrents ssi

1 X n=1(4p(1p))npn=1: Mais cela est vrai ssip= 1=2, auquel cas le numerateur est 4p(1p) = 1 etP1 n=11=n=1. Sip6= 1=2, 4p(1p)<1, et la serie est bornee par une serie geometrique, qui converge.

On a donc:

La ma rcheal eatoireest r ecurrentessi p= 1=2 (la marche est symetrique).On peut denir aussi une marche aleatoire sur les entiers en 2 dimensions ou plus.

On peut prouver qu'une marche symetrique en 2 dimensions est aussi recurrente, mais une ma rcheen 3 dimensions ou plus est toujours transitoir e! Plus la dimension augmente, plus c'est facile de s'evader!

Draft20

Frequences de visites et recurrence positive

La probabilite d'atteindre eventuellementjquand on est ai: f i;j=P[Xn=jpour unn>0jX0=i] =P" 1X n=1I[Xn=j]>0jX0=i# :Proposition.Siiest recurrent eti$j, alorsfi;j= 1.

Preuve.

Puisque i$j, il existe unn>0 tel quep=P(n)

i;j>0. Donc chaque fois qu'on visitei, on visiterajdansnetapes avec probabilite au moinsp. Mais on visiteiinniment souvent. On a donc une innite d'occasions d'aller aj, chaque fois avec probabilite de succes au moinsp. Le nombre de ces occasions que l'on va rater avant le premier succes est une v.a. geometrique(p), donc ce nombre est ni avec probabilite 1.

Draft21

Soitjun etatr ecurrentet X0=j. Letemps de p remierretour ajest R j= minfn1 :Xn=jg; Le temps de r ecurrencemo yen est m j=E[RjjX0=j]: On dit quejestr ecurrentp ositifsi mj<1etr ecurrentnul si mj=1. Proposition.Siiest recurrent positif eti$j, alorsjest recurrent positif aussi. En d'autres mots, la recurrence positive est une propriete de classe. La recurrence nulle aussi.

Preuve.

P arhyp othese,i>0 etP(n)

i;j>0 pour un certainn. DonciP(n) i;j>0. Mais cette valeurs est la proportion des etapes ou on arrive ajet on etait aiil y anetapes, et elle ne peut pas depasser la proportionjdes etapes ou on arrive aj(de n'importe ou). Par consequent,jiP(n)quotesdbs_dbs19.pdfusesText_25

[PDF] chaine de markov matrice de transition

[PDF] chaine d'acquisition de données

[PDF] chaine de mesure audioprothèse

[PDF] acquisition de données du capteur ? l ordinateur

[PDF] chaine de mesure pdf

[PDF] chaine d'acquisition capteur

[PDF] les capteurs exercices corrigés

[PDF] chaine de markov apériodique

[PDF] chaine de markov apériodique exemple

[PDF] chaine de markov reversible

[PDF] chaine de markov récurrente

[PDF] chaine de markov exemple

[PDF] chaine de markov irreductible exemple

[PDF] chaine de markov exercice corrigé

[PDF] chaine énergétique barrage hydraulique