[PDF] [PDF] CHAÎNES DE MARKOV - Institut de Mathématiques de Bordeaux

View - Download [PDF] CHAÎNES DE MARKOV - Institut de Mathématiques de Bordeaux

Previous PDF

Next PDF

CHAÎNES DE MARKOV

Préparation à l"Agrégation Bordeaux 1

Année 2012 - 2013

Jean-Jacques Ruch-Marie-Line Chabanol

Table des Matières

Chapitre I. Chaînes de Markov5

1. Définition5

2. Exemples7

3. La relation de Chapman-Kolmogorov 9

4. Classification des états 12

5. Périodicité13

6. Etats récurrents et transients 14

7. Lois de probabilités stationnaires 18

7.A. Chaînes de Markov à espace d"états fini : lois invariantes 19

7.B. Retour au cas général : états récurrents nuls et états récurrents positifs 22

7.C. Cas général : retour aux mesures stationnaires 23

7.D. Cas général : convergence, théorème ergodique 26

3

CHAPITRE I

Chaînes de Markov

Ce chapitre est fortement inspiré des livres de Bercu (modélisation stochastique et simulation), Toulouse

(Thèmes de probabilités et statistique) et Foata-Fuchs (Processus stochastiques)

Les chaînes de Markov constituent un des exemples les plus simples de suites de variables aléatoires

(Xn). Les variables(Xn)sont à valeurs dans un ensembleEappeléespace d"état. Certaines chaînes de

Markov sont à espace d"états continu, mais nous n"aborderons pas leur étude ici. Nous nous intéresserons

uniquement aux chaînes à espace d"états fini ou dénombrable. Dans toute la suiteEsera donc un ensemble

fini ou dénombrable (Nou un sous-ensemble), que l"on munira de la tribu de toutes ses parties.

1. Définition

Soit(Xn)n0une suite de variables aléatoires à valeurs dans un ensemble au plus dénombrable E. La loi de

la suite(Xn)n0est une loi surENmuni de la tribu engendrée par les cylindres. En vertu d"un théorème

de Carathéodory, la loi de la suite(Xn)n0est caractérisée par ses lois marginales de dimension finie,

c"est-à-dire par la loi des vecteurs aléatoires(X0;:::;Xn)pour toutn2N. Or,Eest au plus dénombrable,

et donc la loi de(X0;:::;Xn)est caractérisée à son tour par la donnée deP(Xn=xn;:::;X0=x0)pour

tout(x0;:::;xn)dansE. Définition 1.Une suite(Xn)n0de variables aléatoires à valeurs dans un ensemble au plus dénombrableEest unechaîne de Markovd"espace d"étatsEsi et seulement si pour toutk2N, pour tout(x0;:::;xk+1)dansEtels queP(Xk=xk;:::;X0=x0)>0,

P(Xk+1=xk+1jXk=xk;:::;X0=x0) =P(Xk+1=xk+1jXk=xk):

Cela s"écrit également

L(Xk+1jXk=xk;:::;X0=x0) =L(Xk+1jXk=xk)

pour toutk2N. La chaîne est ditehomogènesi on a de plus pour toutk2Net toutxetydansE,

P(Xk+1=yjXk=x) =P(X1=yjX0=x):Remarque :En toute rigueur il faudrait faire attention quand les événements par lesquels on conditionne

peuvent être de probabilités nulles. De fait dans les problèmes de modélisation, les chaînes de Markov

sont données par la loi deX0et par toutes les probabilités de transition et les problèmes ne se posent

pas.

L"indicende la suite(Xn)n0est interprété comme un temps. La variableXkreprésente la position

spatiale à l"instantk, la tribu(X0;:::;Xk1)représente son passé tandis que la tribu(Xk+1;Xk+2;:::)

représente son futur. Les chaînes de Markov sont des suites aléatoires sans mémoire, en quelque sorte.

Dans l"évolution au cours du temps, l"état du processus à un instant futur ne dépend que de celui à

l"instant présent, mais non de ses états antérieurs. On dit souvent que conditionnellement au présent, passé et futur sont indépendants.

Dans toute la suite, les chaînes Markov considérées seront toutes homogènes et à espace d"états au plus

dénombrable. 5

6Chapitre I. Chaînes de Markov

Définition 2.On appelleprobabilité de transitionpour aller de l"étatxà l"étatyla probabilité

p

x;y=P(Xk+1=yjXk=x) (=P(X1=yjX0=x)):Lemme 3.On note0la loi deX0(0(x0) =P(X0=x0)). On a alors pour tous(x0;:::;xn)dansE

P(Xn=xn;:::;X0=x0) =0(x0)n1Y

k=0p xk;xk+1:Démonstration.Par conditionnements successifs : P(Xn=xn;:::;X0=x0) =P(X0=x0)P(X1=x1jX0=x0)P(X2=x2jX1=x1;X0=x0):::P(Xn= x njXn1=xn1;:::;X0=x0) =(x0)Qn1 k=0pxk;xk+1: Définition 4.On appellematrice de transitionla matriceP= (px;y)x;y2E: P=0 B @p x0;x0px0;x1px0;x2 p x1;x0px1;x1px1;x2 .........1 C A:

D"après le lemme précédent, la loi d"une chaîne de Markov est caractérisée par la loi0deX0et par

sa matrice de transitition.C"est une matrice finie ou dénombrable, suivant que l"ensemble des états est fini ou dénombrable.

Proposition 5.Toute matrice de transition vérifie les propriétés suivantes : (1)pour tout couple(x;y)deE,0px;y1; (2)pour toutx2E, on aP

y2Epx;y= 1.Démonstration.Les nombrespx;ysont des probabilités, donc le premier point est évident. Le

second point découle du fait qu"on somme les probabilités sur toutes les valeurs possibles d"une variable

aléatoire. Une matrice qui vérifie les deux points ci-dessus est appeléematrice stochastique. Proposition 6.SoitPune matrice stochastique. Alors (1)Padmet1comme valeur propre;

(2)le vecteurVayant toutes ses composantes égales à1est un vecteur propre associé à cette valeur

propre.Démonstration.Il suffit de multiplier la matricePpar le vecteurV. Lemme 7.On identifiera une probabilitésurEet le vecteur ligne dont laième coordonnée est (xi). SoitXnest une chaîne de Markov de matrice de transitionP, et soit0la loi deX0. Alors la loi de X

1est1=0P, et pour tout entiern, la loi deXnestn=0Pn.

En particulier, si la chaîne part dexi,0= (0;:::;0;1;0:::;0)etP(Xn=xj) =P(Xn=xjjX0= x i) =Pni;j.

Jean-Jacques Ruch

2.Exemples7

Démonstration.Pour le premier point, on a pour toutxideE,

P(X1=xi) =P

x j2EP(X1=xijX0=xj)P(X0=xj) =P x j2E0(xj)Pj;i= (0P)i. (en posant par conventionP(AjB)P(B) = 0siP(B) = 0). Ensuite on peut procéder par récurrence. On note(Qn)la propositionn=0Pn. On vient de prouver Q

1. Il reste à vérifier l"hérédité. Soitn >0. On supposen=0Pn. Alors pour toutxideE,

P(Xn+1=xi) =P

x j2EP(Xn+1=xijXn=xj)P(Xn=xj) =P x j2En(j)Pj;i=0Pn+1. Ainsi l"évolution de la loi deXnse ramène en fait à de l"algèbre linéaire.

A toute matrice de transition, on peut associer un graphe dirigé, éventuellement infini. Les sommets du

graphe sont les différents états de la chaîne. Il y a une flèche, étiquetéepx;y, entre le sommetxet le

sommetysi et seulement la probabilité de transition est strictement positive :px;y>0:La chaîne peut

alors s"interpréter comme une marche aléatoire sur le graphe.

On verra plus tard que les composantes fortement connexes du graphe joueront un grand rôle, notamment

les composantes fermées.

2. Exemples

Il y a des modèles classiques de chaînes de Markov homogènes, souvent rencontrés, avec lesquels il est

bon de se familiariser dès le début, en voici quelques-uns.

La chaîne à deux états.

Si on exclut le cas trivial, la matrice de transition correspondante est de la forme P=1 1

0< ; <1:

Elle permet de faire des calculs explicites : pour toutn0, on peut évaluer lanièmepuissancePn, ainsi

que la limitelimnPn(exercice), et donc déterminer explicitement la loi deXn. Le graphe associé est très simple. Il a une seule composante fortement connexe, fermée.1 1

Jean-Jacques Ruch

8Chapitre I. Chaînes de Markov

Le modèle de diffusion d"Ehrenfest

Deux urnesAetBcontiennent, à elles deux ,aboules, numérotées de1àa. A chaque instant, on

choisit une boule de façon uniforme, et on la change d"urne.Xncorrespond alors au nombre de boules

contenues dans l"urneAà l"instantn: l"ensemble des états est donc l"ensembleE=f0;1;:::;ag. Dans

ces conditions, par exemple, si à un instant l"urneAest vide (la chaîne est dans l"état 0), à l"instant

suivant l"urne contiendra 1 boule avec probabilité 1. Si à un instantAcontientiboules,0< i < a, à l"instant suivant elle contiendrai1oui+ 1boules, avec probabilité respectivement ia etdia . La matrice de transition est donc donnée par P=0 B

BBBBBB@0 1 0 00 0 0

1=a0 (a1)=a00 0 0

0 2=a0 (a2)=a0 0 0

0 0 0 0(a1)=a0 1=a

0 0 0 00 1 01

C

CCCCCCA

et le graphe par :Là encore il n"y a qu"une composante fortement connexe.

SiX0=a, le processus(Xn)n0est une description simplifiée de la diffusion d"un gaz d"un récipientA

vers un récipientBinitialement vide (chaque boule représente une molécule).

Promenade au hasard (ou marche aléatoire) surZ

On considère une chaîne de Markov homogène, d"espace d"étatsE=Z=f0;1;2;:::get de matrice de transitionP= (px;y) (x;y2Z), avec pour tout(x;y)2Z2, p x;y=8 :p;sij=i+ 1

1p;sij=i1

0;dans les autres cas

oùpest un nombre fixé tel que0< p <1. Un tel processus est appelé promenade aléatoire (ou marche

aléatoire) surZ. Son graphe peut être décrit comme suit :

Jean-Jacques Ruch

3.La relation de Chapman-Kolmogorov9Là encore, le graphe a une seule composante fortement connexe.

Le modèle de la ruine du joueur

Un joueurAjoue contre un joueurBune suite de parties de pile ou face (avec une pièce éventuellement

pipée), indépendantes. Au départ,Apossèdeaeuros, etB b: la somme totale de leurs fortunes est de

a+beuros. A chaque partie on convient que le joueurAgagne1euro si le résultat est pile, sinon il perd

un euro. La probabilité d"obtenirpileestpavec0< p <1. Le jeu s"arrête dès que l"un des joueurs est

ruiné. Pour chaquen1, on désigne parXnla fortune du joueurAà l"issue de lanièmepartie. La suite

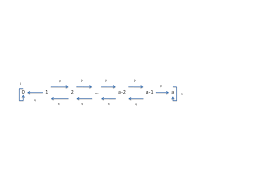
(Xn)n0est une chaîne de Markov, dont l"ensemble des états estE=f0;1;:::;a+bg.

Sa matrice de transition est donnée par

P=0 B

BBBBBB@1 0 0 00 0 0

q0p90 0 0

0q0p:::0 0 0

0 0 0 0q0p

0 0 0 00 0 11

C

CCCCCCA

et son graphe parLes états0(ruine deA) eta+b(ruine deB) sont dits absorbants : quand on est dessus, on n"en sort

plus. Cette fois, le graphe a 3 composantes fortement connexes, dont deux seulement sont fermées.

3. La relation de Chapman-Kolmogorov

On appelle ainsi la propriété qui relie, pour une chaîne de Markov homogène, les probabilités de transition

ennétapes aux probabilités en une seule étape. On note(Xn)n0une chaîne de Markov homogène, dont l"ensemble des états estEet la matrice de transitionP= (pi;j)(i;j)2E2. Pourn0eti;j2Eon désigne parp(n) i;jla probabilité, partant de l"étati à l"instant0, d"être dans l"étatjà l"instantn; en d"autres termes on a : p (n) i;j=P(Xn=jjX0=i)

Comme on l"a vu dans le lemme 7,p(n)

i;jcorrespond àPn(i;j).

On peut facilement vérifier :

Proposition 8.Pour toutn0la matricePnest stochastique.

Jean-Jacques Ruch

10Chapitre I. Chaînes de Markov

Démonstration.En effet, pour touti2E, on a :X

j2Ep(n) i;j=X j2EP(Xn=jjX0=i) = 1:

Ainsi, pour toutk1fixé, la suite(Xkn)n0est une chaîne de Markov, ayant même ensemble d"étatsE

et dont la matrice de transition estPk.

La relation de Chapman-Kolmogorov qui suit peut s"interpréter en disant que "pour passer deiàjen

m+nétapes il a bien fallu enmétapes aller deià un certainkpuis ennétapes aller dekàj.

Proposition 9. Relation de Chapman-Kolmogorov

Pour tout(i;j)2E2et tout couple(m;n)d"entiers positifs, on a l"identité :

P(Xm+n=jjX0=i) =X

k2EP(Xm=kjX0=i)P(Xn=jjX0=k) ou encore p(m+n) i;j=X k2Ep(m) i;kp(n)

k;j:Démonstration.Cette identité résulte immédiatement de l"associativité du produit matricielle :

P (m+n)=Pm+n=PmPn=P(m)P(n): Les propositions suivantes sont des raccourcis de calcul souvent utiles :

Proposition 10.Soientn0,r1deux entiers. Alors

P(Xn+r=jn+r;:::Xn+1=jn+1jXn=in:::X0=i0) =P(Xn+r=jn+r;:::Xn+1=jn+1jXn=in)

=pin;jn+1pjn+1;jn+2:::pjn+r1;jn+rDémonstration.C"est immédiat à partir par exemple du lemme 3.

Les relations qui caractérisent les chaînes de Markov peuvent s"écrire d"une autre manière, équivalente

à celles données précédemment. Plus formellement, on peut généraliser : NotonsAun événement

appartenant à la tribu du passéFn1=(X0;:::;Xn1). Il s"écrit donc comme une réunion dénombrable

d"événements disjoints deux à deux de la formefX0=i0;:::;Xn1=in1g. SoitA+un événement

appartenant à la tribu du futur(Xn+1;Xn+2;:::). On obtient alors en corollaire du résultat précédent :

Théorème 11.Avec les mêmes hypothèses que ci-dessus, siP(AetXn=i)>0, alors : P(A+jAetXn=i) =P(A+jXn=i)Par exemple,P(X5=ijX3=jetX1=k) =P(X5=ijX3=j) =P2j;i.

Par la propriété d"homogénéité, on peut ensuite se ramener à un conditionnement parX0; une manière

de dire cela proprement est que conditionnellement àXn=x, la suite(Xn+m;m2N)est une chaîne de

Markov de même matrice de transition que(Xn), de loi initialex(et indépendante de(X0;:::;Xn1)).

Jean-Jacques Ruch

3.La relation de Chapman-Kolmogorov11

Notation: on notera, siAest un événement etZune variable aléatoire,Px(A) =P(AjX0=x)et E

x[Z] =E[ZjX0=x]: cela consiste à travailler non pas avec(Xn)mais avec la chaîne de même matrice

de transition que(Xn)et de loi initialex. On l"appelle aussi "chaîne issue dex".

On va voir que la relation précédente, démontrée pourndéterministe, est en fait vraie pour tout temps

d"arrêtTadapté à la filtration naturelle des(Xn).

SoitTun temps d"arrêt adapté à la suite(Xn)n0(relativement à la filtration naturelle). Rappelons

qu"un événementA2 F1(tribu engendrée par la réunion deFn) appartient à la tribuFT, s"il a la

propriété suivante

8n0; A\ fT=ng 2 Fn:

Théorème 12.Propriété de Markov forte

SoitTun temps d"arrêt à valeurs dans[0;+1]adapté à la chaîne de Markov(Xn)n0, d"ensemble d"étatsEet de matrice de transitionP= (pi;j)(i;j)2E2. Soientiun élément de EetAun élément de la tribuFTtel queP(T <+1;A;XT=i)>0. Alors on a l"identité : P(XT+1=j1;:::;XT+r=jrjT <+1;A;XT=i) =P(X1=j1;:::;Xr=jrjX0=i) =pi;j1pj1;j2:::pjr1;jr:Démonstration.PosonsA0=fT <+1;A;XT=ig,B=fXT+1=j1;:::;XT+r=jrg, et B n=fXn+1=j1;:::;Xn+r=jrgpourn0. Il s"agit de prouver :

P(BjA0) =pi;j1pj1;j2:::pjr1;jr:

ou encore queP(A0\B) =pi;j1pj1;j2:::pjr1;jrP(A0). On a :

P(A0\B) =X

n0P(T=n;A;XT=i;B) =X n0P(T=n;A;Xn=i;Bn) 0X n0P(BnjT=n;A;Xn=i)P(T=n;A;Xn=i): où dans la dernière somme on n"a gardé (

P0) que les termes tels queP(T=n;A;Xn=i)>0. Pour

ces termes, puisquefT=n;Ag 2 Fnon peut appliquer la propriété de Markov (déterministe) vu précédemment. On a donc P(BnjT=n;A;Xn=i) =P(BnjXn=i) =P(Xn+1=j1;:::;Xn+r=jrjXn=i) =pi;j1pj1;j2:::pjr1;jr

On en déduit que

P(A0\B) =pi;j1pj1;j2:::pjr1;jrX

n0P(T=n;A;Xn=i) =pi;j1pj1;j2:::pjr1;jrP(T <+1;A;XT=i) et donc le résultat.

Cette formule est particulièrement utile, lorsqu"on prend pour temps d"arrêt le temps d"atteinteTi=

inffn1=Xn=igde la chaîne pour l"étati. SiTi<1, on a automatiquementXTi=i; donc la formule devient : P(XTi+1=j1;:::;XTi+r=jrjTi<+1;A) =P(X1=j1;:::;Xr=jrjX0=i) =pi;j1pj1;j2:::pjr1;jr:

On en tire le corollaire suivant, très utile :

Jean-Jacques Ruch

12Chapitre I. Chaînes de Markov

Corollaire 13.SoitTi= inffn1 :Xn=ig. Conditionnellement à l"événementfTi<+1g, la

suite translatée(XTi+n)n0est un chaîne de Markov de matrice de transitionPet d"état initiali. De

plus cette suite est indépendante de la tribuFT.4. Classification des états

Nous allons définir une classification des états et en déduire des propriétés des chaînes de Markov. Les

états d"une chaîne de Markov se répartissent en classes que l"on définit à partir de la matrice de transition.

Définition 14.On dit que l"étatjestaccessibleà partir de l"étati, s"il existe un entiern0tel que

p (n) i;j>0. On notei j.

Sur le graphe, sii6=j,i js"il existe un chemin (orienté) du sommetivers le sommetj.Proposition 15.La relation d"accessibilité entre états est réflexive et transitive.Démonstration.Commep(0)

i;i=P(X0=ijX0=i) = 1pour tout étati, la relation est réflexive.

Ensuite, sii jetj l, alorsp(m)

i;j>0etp(n) j;l>0pour certains entiersm; n0. D"après le corollaire

9, on a :

P(Xm+n=ljX0=i) =X

k2EP(Xm=kjX0=i)P(Xn=ljX0=k)p(m) i;jp(n) j;l>0 d"oùi l. Proposition 16.Soienti; jdeux états; les deux propriétés suivantes sont équivalentes : a) l"état jest accessible à partir de l"étati, soiti j b)

le pr ocessus,p artantde i, passe parjavec probabilité strictement positive.Démonstration.D"abord, a))b) est évident. Pour l"autre implication, montrons non a))non

b). On a donc pour toutn0,p(n) i;j= 0. SoitAl"événement "le processus passe parj". On a

P(AjX0=i) =P([n0fXn=jgjX0=i)X

n0P(Xn=jjX0=i) =X n0p(n) i;j= 0: d"où la propriété b). Définition 17.On dit que les étatietjcommuniquentet on écriti jsi on a à la foisi jet

j i.Proposition 18.La relation de "communication" est une relation d"équivalence.Démonstration.Les propriétés de réflexivité et de transitivité étant déjà vérifiées pour la relation

d"accessibilité, elles restent naturellement encore valables pour la nouvelle relation. Enfin, cette dernière

est symétrique par construction.

Jean-Jacques Ruch

5.Périodicité13

Comme on a toujoursp(0)

i;i= 1, tout état communique avec lui même.

Les classes d"équivalence de cette relation sont les composantes fortement connexes du graphe. On les

appelle souventcomposantes irréductiblesou classes irréductibles.

SiC1etC2sont deux classes distinctes, on peut éventuellement aller, disons deC1àC2, mais on ne peut

alors retourner deC2àC1. En revanche, tous les états d"une même classe communiquent.

Certaines classes peuvent ne comporter qu"un seul élément : c"est par exemple le cas siiunétat absorbant

i.e.pi;i= 1(ce qui entraîne pourn0p(n) i;i= 1).

Une classeC1telle que8i2C1;8j =2C1;pi;j= 0est une classeclose: sur le graphe, cela signifie qu"aucune

arête ne sort de la classe. Définition 19.S"il n"y a qu"une seule classe pour la relation de communication, autrement dit, si tous les états communiquent entre eux, la chaîne est dite irréductible.Exemple 0. La marche aléatoire surZest irréductible (tous les états communiquent)

Exemple 1.

Considérons la chaîne de Markov, dont l"ensemble des états estE=f0;1;2g, la matrice de transition

P=0 @1=2 1=2 0

1=2 1=4 1=4

0 1=3 2=31

A Cette chaîne est irréductible. Tous les états communiquent, même sip0;2=p2;0= 0.

Exemple 2.

Considérons la chaîne de Markov, dont l"ensemble des états estE=f0;1;2;3g, la matrice de transition

P=0 B

B@1=2 1=2 0 0

1=2 1=2 0 0

1=4 1=4 1=4 1=4

0 0 0 11

C CA

La chaîne comporte trois classef0;1g,f2getf3g. L"état3est absorbant, l"état2n"est plus visité après

un certain temps. On va voir que les classesf0;1getf3gsont récurrentes alors que la classef2gest transiente.

5. Périodicité

Il s"agit d"étudier dans quelles conditions le temps qui sépare deux retours au même étatjest ou n"est

pas multiple d"un temps minimum. Pour ce faire, on introduit la notion depériode. Définition 20.Soitj2E. On appellepériodedej, et on noted(j), le P.G.C.D. de tous les entiers n1pour lesquelsp(n) j;j>0(par convention,pgcd(;) = +1) d(j) =pgcd(n1;p(n) j;j>0) Sid(j) =d2, on dit quejest périodique de périoded. Sid(j) = 1, on dit quejestapériodique.

Une chaîne apériodique est une chaîne de dont tous les états sont apériodiques.En particulier, sipii>0(le graphe possède alors une boucle),iest apériodique.

Jean-Jacques Ruch

14Chapitre I. Chaînes de Markov

Théorème 21.Siiest périodique de périodedfinie et sii j(j6=i), alorsjest aussi périodique de

périoded: la périodicité est une propriété de classe.Démonstration.Sii j, alors il existe deux entiersnetmtels quep(n)

i;j>0etp(m) j;i>0. Comme iest de périoded(i) =d, il existe un entiers1(sest un multiple ded1) tel quep(s) i;i>0. On a donc p (m+s+n) j;jp(m) j;ip(s) i;ip(n) i;j>0. Commep(s) i;i>0entraînep(2s) i;i>0, on a aussip(m+2s+n) j;j>0. La période

dejdivise donc à la foism+s+netm+ 2s+n, donc aussi leur différences. En particulier elle divise

la périoded(i)dei. De la même façon on montre qued(i)divised(j)et donc qued(i) =d(j).

Exemple 1.

Considérons la chaîne de Markov, dont l"ensemble des états estE=f0;1;2g, la matrice de transition

P=0 @0 1 0 p0 1p

1 0 01

A avec0< p <1.

On vérifie avec le graphe qu"il y a une seule classe (récurrente), la chaîne est irréductible. Tous les états

communiquent. De plus les lacets0!1!0et0!1!2!0ont pour longueur2et3; leur P.G.C.D.

estd= 1. L"état0est donc apériodique. Par conséquent, les états1et2sont aussi apériodiques.

Exemple 2.

Considérons la chaîne de Markov, dont l"ensemble des états estE=f0;1;2;3g, la matrice de transition

P=0 B

B@0 0 1=2 1=2

1 0 0 0

quotesdbs_dbs7.pdfusesText_13

[PDF] chaine de markov matrice de transition

[PDF] chaine d'acquisition de données

[PDF] chaine de mesure audioprothèse

[PDF] acquisition de données du capteur ? l ordinateur

[PDF] chaine de mesure pdf

[PDF] chaine d'acquisition capteur

[PDF] les capteurs exercices corrigés

[PDF] chaine de markov apériodique

[PDF] chaine de markov apériodique exemple

[PDF] chaine de markov reversible

[PDF] chaine de markov récurrente

[PDF] chaine de markov exemple

[PDF] chaine de markov irreductible exemple

[PDF] chaine de markov exercice corrigé

[PDF] chaine énergétique barrage hydraulique