[PDF] Comportement dune suite On peut conjecturer la faç

View - Download Comportement dune suite

Previous PDF

Next PDF

http://www.maths-videos.com 1

Comportement d"une suite

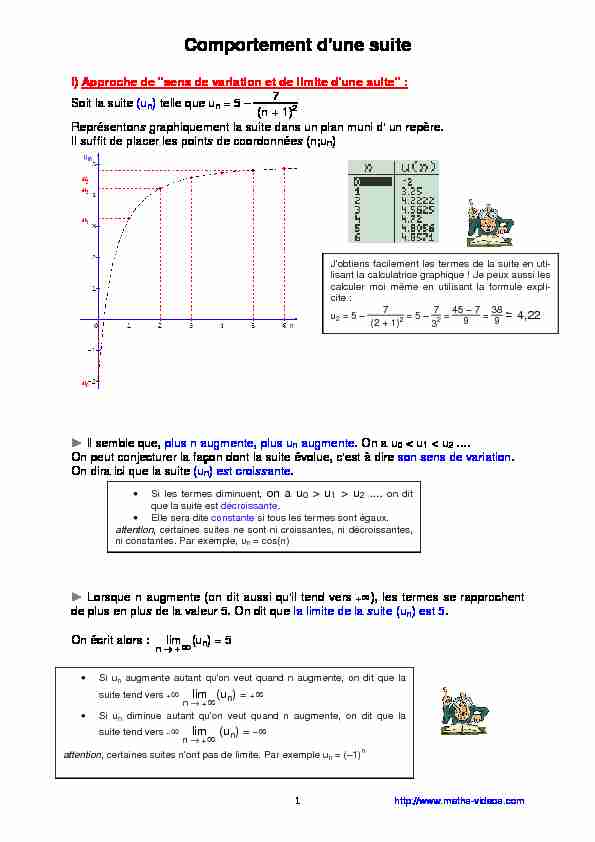
I) Approche de "sens de variation et de limite d"une suite" :

Soit la suite (un) telle que un = 5 - 7

(n + 1)2 Représentons graphiquement la suite dans un plan muni d" un repère. Il suffit de placer les points de coordonnées (n;u n) ► Il semble que, plus n augmente, plus un augmente. On a u0 < u1 < u2 .... On peut conjecturer la façon dont la suite évolue, c"est à dire son sens de variation.

On dira ici que la suite

(un) est croissante. ► Lorsque n augmente (on dit aussi qu"il tend vers +), les termes se rapprochent de plus en plus de la valeur 5. On dit que la limite de la suite (un) est 5.

On écrit alors : lim

n ® +(un) = 5 J"obtiens facilement les termes de la suite en uti- lisant la calcula trice graphique ! Je peux aussi les calculer moi même en utilisant la formule expli- cite : u

2 = 5 - 7

(2 + 1)2 = 5 - 7

32 = 45 - 7

9 = 38

9 4,22

· Si les termes diminuent, on a u0 > u1 > u2 .... on dit que la suite est décroissante.

· Elle sera dite

constante si tous les termes sont égaux. attention , certaines suites ne sont ni croissantes, ni décroissantes, ni constantes. Par exemple, un = cos(n) · Si un augmente autant qu"on veut quand n augmente, on dit que la suite tend vers + limn ® +(un) = +

· Si u

n diminue autant qu"on veut quand n augmente, on dit que la suite tend vers - limn ® + (un) = - attention, certaines suites n"ont pas de limite. Par exemple u n = (-1)n http://www.maths-videos.com 2

II) Sens d"une variation de suite :

définition : une suite (un) est : strictement croissante si et seulement si, pour tout entier naturel n, un < un+1 Ex : la suite (v n) des nombres impairs 1, 3, 5, 7, 9.... est une suite strictement croissante

C"est la suite arithmétique de premier terme v

0 = 1 et de raison 2

strictement décroissante si et seulement si, pour tout entier naturel n, un > un+1 Ex : la suite (w n)n1 des nombres 1, 1 2 , 1 3 , 1 4, 1

5.... est une suite strictement décroissante

C"est la suite telle que w

n = 1 n pour tout entier naturel supérieur ou égal à 1 constante si et seulement si, pour tout entier naturel n, un = un+1 définition : une suite (un) est monotone lorsqu"elle est soit croissante, soit décrois- sante , soit constante. Ex : ► les suites (vn) et (wn)n1 définies précédemment sont monotones. ► la suite (un) définie pour tout entier naturel n par un=(-1)n n"est pas monotone

III) Etudier le sens d"une variation de suite :

Soit (u

n) une suite définie sur il existe trois façons éventuelles de procéder : ► On peut étudier le signe de la différence un+ 1 - un

· si, pour tout entier naturel n,

un+1 - un 0 alors la suite un est croissante · si, pour tout entier naturel n, un+1 - un 0 alors la suite un est décroissante justification : u n+1 - un 0 équivaut à un+1 un et (un) est croissante u n+1 - un 0 équivaut à un+1 un et (un) est décroissante Ex : Soit la suite (un) définie pour tout entier naturel n par un = 2 + 1 n+1

Etudions le sens de variation de (u

n) n+1 = 2 + 1 n+2 - 2 - 1 n+1 = n+1 ( )n+1( )n+2 - n+2( )n+1( )n+2 -1 ( )n+1( )n+2 -1 < 0 et (n+1)(n+2) > 0 donc un+1 - un < 0 et la suite ( )un est strictement décroissante

on définit de la même façon une suite croissante ou décroissante en utilisant les inégalités au sens large.

(wn)n1 est une suite décroissante car pour tout entier naturel n, wn wn+1 http://www.maths-videos.com 3 ► On peut comparer un+1 un à 1 (uniquement si tous les termes de la suite sont strictement positifs)

· si, pour tout entier naturel n, un+1

un 1 alors la suite un est croissante

· si, pour tout entier naturel n, un+1

un 1 alors la suite un est décroissante justification : u n+1 un 1 équivaut à un+1 un et un est donc croissante u n+1 un 1 équivaut à un+1 un et un est donc décroissante Ex : Soit la suite (un) définie pour tout entier naturel n par un = 2 n 3n+2

Etudions le sens de variation de (u

n) un+1 un= 2n+1 3n+3 2n 3n+2 = 2 n+1

3n+3 x 3

n+2

2n = 2

3 or, 2 3 < 1 donc ( )un est décroissante ► Si la suite (un) est définie à l"aide d"une fonction par un=(n), on peut utiliser le sens de variation de la fonction.

· si la fonction

est croissante sur [0 ; +[, alors la suite est croissante

· si la fonction

est décroissante sur [0 ; +[, alors la suite est décroissante justification :

· Si f est croissante sur

[0 ; +[, (n+1) n équivaut à (n+1) (n) donc un+1 un (la suite (un) est donc croissante)

· Si f est décroissante sur

[0 ; +[, (n+1) n équivaut à (n+1) (n) donc un+1 un (la suite (un) est donc décroissante) Ex : Soit la suite (un) définie pour tout entier naturel n par un = 3n2

Etudions le sens de variation de (u

n)

La fonction u

n est définie par un = (n) avec (x) = 3x2

La fonction

est croissante sur [0 ; +[ donc ( )un est croissante. propriété : · une suite arithmétique de raison r est croissante si r>0 et décroissante si r<0

· la suite (v

n) telle que vn = qn pour tout entier naturel n est croissante si q>1 et décroissante si 0· Soit (u n) une suite arithmétique de raison r.

Par définition, on a u

n+1 = un + r donc un+1 - un = r - si r > 0, on a u n+1 - un > 0 donc la suite est croissante - si r < 0, on a u n+1 - un < 0 donc la suite est décroissante n"oublions pas que un>0 ! http://www.maths-videos.com 4 · Soit (vn) une suite telle que vn= qn avec q0.

Par définition, on a v

n+1 = qn+1 = qn x q = vn x q donc q = vn+1 vn - si q>1, v n+1 vn >1 donc vn+1 > vn donc la suite est croissante - si 0IV) Notion de limite d"une suite : a) suite ayant pour limite + (ou -) (limite infinie) :

Soit la suite (u

n) définie pour tout entier naturel n par un = n 2 10 b) suite ayant pour limite un nombre réel (limite finie) :

Soit la suite (u

n)n1 définie pour tout entier naturel n par un = 1 n2 + 3 Je prends un nombre réel A, aussi grand que je le veux.

Je trouve alors un rang

n0 à partir duquel tous les termes de la suite seront plus grands que A Démontrer ce qui précède quel que soit le nombre A, c"est démontrer que les termes u n de la suite sont tous aussi grands qu"on veut à condition de prendre n assez grand.

On dit que la suite (u

n) a pour limite + et on note : limn ® +(un) = +

De la même façon, on pourra montrer qu"une

suite tend vers - . Pour un nombre réel A (aussi petit qu"on veut), il existe un rang à partir duquel tous les termes de la suite sont inférieurs à A. A 1 1 0 1 A n0 un n

Je conjecture que la limite de la suite est 3

(à l"aide de ma calculatrice)

Je choisis un nombre réel positif

a aussi petit que je veux !

Je trouve alors un rang

n0 à partir duquel tous les termes de la suite seront dans l"in- tervalle ]3 - a ; 3 + a[ Démontrer ce qui précède quel que soit le réel positif a, c"est démontrer que les ter- mes u n de la suite finissent par s"accumu- ler près de 3

On dit que la suite (u

n) a pour limite 3 et on note : limn ® +(un) = 3 01 1 un 3 3 + a 3 - a n0 http://www.maths-videos.com 5 n un

Certaines suites n"ont pas de li-

mite !

Par exemple, la suite

(un) définie pour tout entier naturel n par un = cos(n)quotesdbs_dbs29.pdfusesText_35

[PDF] couche electronique

[PDF] pilote brother dcp 7055w

[PDF] brother dcp-j172w driver

[PDF] plat typique des asturies

[PDF] technique de conservation des aliments les plus anciennes

[PDF] comment conserver les aliments au moyen age

[PDF] technique de conservation des aliments au fil du temps

[PDF] conservation du sel

[PDF] conservation des aliments dans l'antiquité

[PDF] conservation viande séchée

[PDF] culture de l'ail en afrique pdf

[PDF] vertue de l ail en pdf

[PDF] fiche technique ail

[PDF] les vertus de l'ail et de l'oignon pdf

[PDF] fiche technique ail pdf