 LES SUITES NUMERIQUES
LES SUITES NUMERIQUES
( la table de la calculatrice permet de conjecturer le sens de variation d'une suite). Méthode 1 : (la plus utilisée). On calcule la différence en fonction.
 Comportement dune suite
Comportement dune suite
On peut conjecturer la façon dont la suite évolue c'est à dire son sens de variation. On dira ici que la suite (un) est croissante.
 LA CALCULATRICE POUR CONJECTURER ET VÉRIFIER LES
LA CALCULATRICE POUR CONJECTURER ET VÉRIFIER LES
c) Construire le tableau de variations de f. 3) a) Recopier et compléter le tableau suivant où les valeurs numériques de f (x) seront arrondies à 10.
 Première S - Comportement dune suite Problèmes
Première S - Comportement dune suite Problèmes
2) Méthodes pour étudier le sens de variation d'une suite on étudie les variations de la fonctions sur [0 ; +? [ ... Prouver la conjecture faite au 2.
 Calculatrice TI 82 stats.fr Suites
Calculatrice TI 82 stats.fr Suites
Pour calculer les termes et représenter graphiquement une suite la calculatrice doit être en Conjecturer le sens de variation et la limite de la suite.
 VARIATIONS DUNE FONCTION
VARIATIONS DUNE FONCTION
On dit qu'une fonction croissante conserve l'ordre et qu'une fonction décroissante renverse l'ordre. Exercice : Déterminer les variations d'une fonction. Vidéo
 Variations dune suite Suite croissante - Décroissante - Premi`ere S
Variations dune suite Suite croissante - Décroissante - Premi`ere S
Pour chaque suite définie ci-dessous calculer les premiers termes `a la main
 Exercice 1 : (4 points) Etudier la monotonie de la suite u. 1) un = n
Exercice 1 : (4 points) Etudier la monotonie de la suite u. 1) un = n
À l'aide de la calculatrice conjecturer le sens de variations de la suite. (un) ainsi que sa limite éventuelle. On considère la suite (vn) définie pour
 CONTINUITÉ DES FONCTIONS
CONTINUITÉ DES FONCTIONS
Les flèches obliques d'un tableau de variation traduisent la continuité et la stricte c) À l'aide du graphique conjecturer la limite de la suite (un).
 Calculatrice Casio Graph 35+ Suites
Calculatrice Casio Graph 35+ Suites
Conjecturer le sens de variation et la limite de la suite. Déterminer une valeur approchée de u100 . Exercice 2. On considère la suite définie par vn = 2 +
 Chapitre 1 METHODES SUR LES SUITES - editions-ellipsesfr
Chapitre 1 METHODES SUR LES SUITES - editions-ellipsesfr
1) Conjecturer le comportement d’une suite 2) Raisonner par récurrence 3) Utiliser les suites arithmétiques et géométriques 4) Étudier le comportement global d’une suite 5) Étudier le comportement asymptotique d’une suite 6) Déterminer des résultats expérimentaux 1 Comment conjecturer le comportement d’une suite
 Exercices corrigés – Suites – Spécialité mathématiques
Exercices corrigés – Suites – Spécialité mathématiques
Variations d’une suite arithmétique Soit (u n) une suite arithmétique de raisonr Alors : — sir >0uest strictement croissante; — sir
 Variations d’une suite
Variations d’une suite
Variations d’une suite et signe de u n+1 u n Pour chaque suite d e nie ci-dessous calculer les premiers termes a la main conjecturer le sens de variations puis d emontrer la conjecture en etudiant le signe de u n+1 u n 1 (u n) est la suite d e nie pour tout entier naturel n par u n = n 3n 2 (u n) est la suite d e nie pour tout entier
Comment conjecturer le sens de variation de la suite ?
Conjecturer le sens de variation de la suite (un). Déterminer le signe du trinôme du second degré : ? x2 + 2x ? 2 . Démontrer votre conjecture. un + 1 = 0, 9un + 1, 2. On considère la suite (vn) définie pour tout entier naturel n par vn = un ? 12. Démontrer que la suite (vn) est une suite géométrique dont on précisera le premier terme et la raison.
Comment calculer les variations de la suite ?
Dans chaque cas, préciser la fonction f, étudier ses variations sur [0, + ?[ et en déduire les variations de la suite. On considère la suite (un) définie pour tout entier naturel n par un + 1 = ? u2 n + 3un ? 2 et u0 = 1. Calculer u1, u2 et u3 . Conjecturer le sens de variation de la suite (un).
Quel est le sens de variation d'une suite ?
Découvrir la notion de sens de variation pour les suites. Étudier le sens de variation d'une suite. Une suite est croissante sur lorsque pour tout n . Une suite est décroissante sur lorsque pour tout n . On étudie le signe de . Lorsque , on étudie le sens de variation de la fonction f. Lorsque , on étudie la position du quotient par rapport à 1.
Comment pouvez-vous déterminer le sens de variation d'une suite?
Dans chaque cas, préciser f, étudier ses variations sur [ 0 ; + ? [ et en déduire les variations de la suite. On admet que les suites ci-dessous ont tous leurs termes strictement positifs. En comparant le quotient u n + 1 u n à 1, étudier le sens de variations des suites.
1 sur 11
Yvan Monka - Académie de Strasbourg - www.maths-et-tiques.frVARIATIONS D'UNE FONCTION
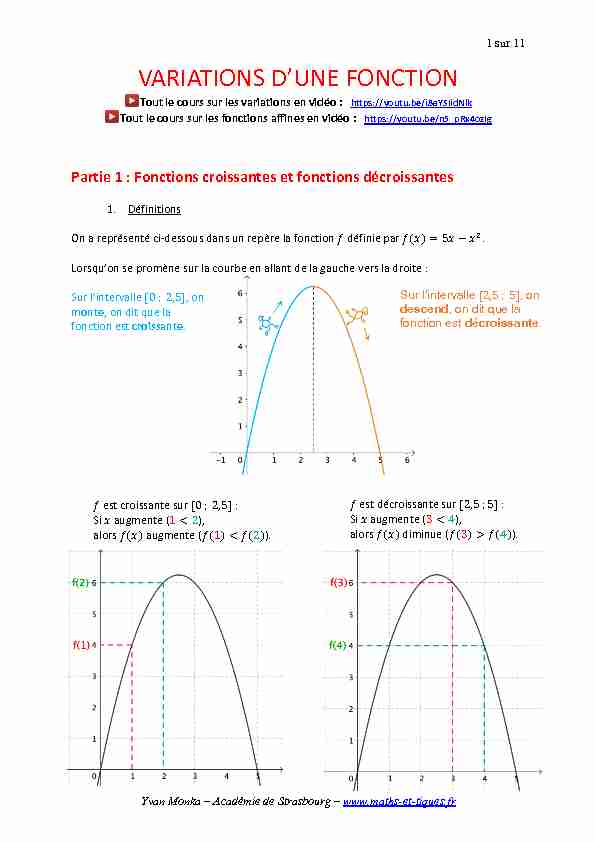
Tout le cours sur les variations en vidéo : https://youtu.be/i8aYSIidNlk Tout le cours sur les fonctions affines en vidéo : https://youtu.be/n5_pRx4ozIg Partie 1 : Fonctions croissantes et fonctions décroissantes1. Définitions
On a représenté ci-dessous dans un repère la fonction ��� définie par ��� =5���-��� Lorsqu'on se promène sur la courbe en allant de la gauche vers la droite :Sur l'intervalle [0;2,5], on
monte, on dit que la fonction est croissante.Sur l'intervalle [2,5;5], on
descend, on dit que la fonction est décroissante. ��� est décroissante sur 2,5;5Si ��� augmente (3<4),
alors ���(���) diminue (���(3)>���(4)). ��� est croissante sur 0;2,5Si ��� augmente (1<2),
alors ���(���)augmente (���(1)<���(2)).2 sur 11
Yvan Monka - Académie de Strasbourg - www.maths-et-tiques.frDéfinitions : Sur un intervalle ���,
- une fonction ��� est croissante, - une fonction ��� est décroissante, si ���<��� alors ��� . si ���<��� alors ���Remarques :
• Pour une fonction ��� constante : on a toujours ��� • Dire que ��� est monotone signifie que ��� est soit croissante, soit décroissante. • On dit qu'une fonction croissante conserve l'ordre et qu'une fonction décroissante renverse l'ordre. Exercice : Déterminer les variations d'une fonctionVidéo https://youtu.be/zHYaPOWi4Iw
Vidéo https://youtu.be/__KaMRG51Ts
2. Maximum et minimum
Exemple : On reprend la fonction ��� définie dans l'exemple de la partie 1.Sur l'intervalle [0;5], on a : ���
2,5 =6,25. On dit que 6,25 est le maximum de la fonction ���. Ce maximum est atteint en 2,5.3 sur 11
Yvan Monka - Académie de Strasbourg - www.maths-et-tiques.frDéfinitions : Sur un intervalle ���,
- une fonction ��� admet un maximum ��� en ���, si pour tout ���, ��� - une fonction ��� admet un minimum ��� en ���, si pour tout ���,���Remarque : Un minimum ou un maximum
s'appelle un extremum.TP avec Python :
Approcher un extremum par la méthode du balayage3. Tableau de variations
Un tableau de variations résume les variations d'une fonction en faisant apparaître les intervalles où elle est monotone. Méthode : Déterminer graphiquement les variations d'une fonction et dresser le tableau de variationsVidéo https://youtu.be/yGqqoBMq8Fw
On considère la représentation graphique la fonction ��� :4 sur 11
Yvan Monka - Académie de Strasbourg - www.maths-et-tiques.fr a) Sur quel intervalle la fonction ��� est-elle définie ? b) Donner les variations de la fonction. c) Donner les extremums de la fonction en précisant où ils sont atteints. d) Résumer les résultats précédents dans un tableau de variations.Correction
a) La fonction ��� est définie sur [-5;7]. b) La fonction ��� est croissante sur les intervalles [-4;0] et [5;7]. Elle est décroissante sur les intervalles [-5;-4] et [0;5]. c) Le maximum de ��� est 3,5. Il est atteint en ���=0. Le minimum de ��� est -4. Il est atteint en ���=-4 . d)Partie 2 : Cas des fonctions affines
1. Définitions
Définitions : Une fonction affine ��� est définie sur ℝ par ��� =������+���, où ��� et ��� sont deux nombres réels. Lorsque ���=0, la fonction ��� définie par ��� =������ est une fonction linéaire.Exemples :
• Fonction affine : ��� =-���+6 • Fonction linéaire : ���2. Variations
Propriété : Soit ���une fonction affine définie sur ℝpar ���Si ���>0, alors ��� est croissante.
Si ���<0, alors ��� est décroissante.
Si ���=0, alors ��� est constante.
Démonstration :
Soient ��� et ��� deux nombres réels tels que ���<���.On sait que ���<��� donc ���-���>0.
Le signe de ���
est le même que celui de ���.5 sur 11
Yvan Monka - Académie de Strasbourg - www.maths-et-tiques.fr - Si ���>0, alors ��� > 0 soit ���Donc ��� est croissante.
- Si ���=0, alors ��� = 0 soit ���Donc ��� est constante.
- Si ���<0, alors ��� < 0 soit ���Donc ��� est décroissante.
Méthode : Déterminer les variations d'une fonction affineVidéo https://youtu.be/9x1mMKopdI0
Déterminer les variations des fonctions affines suivante : a) ��� =3���+2 b) ��� =7-6��� c) ℎCorrection
1) ���
=3���+2 ���>0 donc ��� est croissante.2) ���
=7-6���=-6���+7 ���<0 donc ��� est décroissante.3) ℎ
=-���=-1��� ���<0 donc ℎ est décroissante.3. Représentation graphique
Propriétés :
- Une fonction affine est représentée par une droite. - Une fonction linéaire est représentée par une droite passant par l'origine du repère. Soit la fonction affine ��� définie par ���(���)=������+���. ��� s'appelle le coefficient directeur ��� s'appelle l'ordonnée à l'origine. Méthode : Déterminer graphiquement une fonction affineVidéo https://youtu.be/OnnrfqztpTY
Vidéo https://youtu.be/fq2sXpbdJQg
Vidéo https://youtu.be/q68CLk2CNik
Déterminer graphiquement l'expression des fonctions ��� et ��� représentées respectivement
par les droites (d) et (d').6 sur 11
Yvan Monka - Académie de Strasbourg - www.maths-et-tiques.frCorrection
Ce nombre s'appelle le coefficient directeur.
Si on avance de 1 : on monte de ���.
Ce nombre s'appelle l'ordonnée à l'origine.
-��� se lit sur l'axe des ordonnées.Pour (d) : Le coefficient directeur est 2
L'ordonnée à l'origine est -2
L'expression de la fonction ��� est : ���
=2���-2Pour (d') : Le coefficient directeur est -0,5
L'ordonnée à l'origine est -1
L'expression de la fonction ��� est : ���
=-0,5���-1 Propriété des accroissements : Soit la fonction affine ��� définie sur ℝ par ��� =������+��� et deux nombres réels distincts ��� et ���.Alors : ���=
Démonstration :
Comme ���≠���, et on a : ���=
Remarque : Dans le calcul de ���,inverser ��� et��� n'a pas d'importance.En effet :
Méthode : Déterminer l'expression d'une fonction affineVidéo https://youtu.be/ssA9Sa3yksM
Vidéo https://youtu.be/0jX7iPWCWI4
Déterminer par calcul une expression de la fonction ��� telle que : ���(-2)=4 et ���(3)=1.7 sur 11
Yvan Monka - Académie de Strasbourg - www.maths-et-tiques.frCorrection
��� est une fonction affine, donc elle s'écrit sous la forme : ��� • Calcul de ��� : On a ���(-2)=4 et ���(3)=1, donc d'après la propriété des accroissements :Donc : ���
• Calcul de b :On a par exemple : ���(3)=1, donc :
×3+���=1
+���=1 ���=1+ 9 5 5 5 9 5 • D'où : ���Partie 3 : Cas des fonctions de référence
1. Variations de la fonction carré
Vidéo https://youtu.be/B3mM6LYdsF8
Propriété :
La fonction carré est décroissante sur l'intervalle -∞;0 et croissante sur l'intervalle0;+∞
8 sur 11
Yvan Monka - Académie de Strasbourg - www.maths-et-tiques.frDémonstration au programme :
Vidéo https://youtu.be/gu2QnY8_9xk
On pose : ���
- Soit ���et ��� deux nombres réels quelconques positifs tels que ���<���. Or ���-���>0, ���≥0 et ���≥0 donc ��� ≥0 ce qui prouve que ��� est croissante sur l'intervalle0;+∞
- La décroissance sur l'intervalle -∞;0 est prouvée de manière analogue en choisissant ���et ���deux nombres réels quelconques négatifs tels que ���<���.2. Variations de la fonction inverse
Vidéo https://youtu.be/Vl2rlbFF22Y
Propriété :
La fonction inverse est décroissante sur
l'intervalle -∞;0 et décroissante sur l'intervalle0;+∞
Démonstration au programme :
Vidéo https://youtu.be/cZYWnLA30q0
On pose : ���
- Soit ��� et ��� deux nombres réels strictement positifs avec ���<���. 0 0'/ 0/ Or ���>0, ���>0 et ���-���<0. Donc ��� f est ainsi décroissante sur l'intervalle0;+∞
- La décroissance sur l'intervalle -∞;0 est prouvée de manière analogue. Propriété : Si ��� et ��� sont deux nombres réels de même signe, on a alors : 1 1 En effet, la fonction inverse étant décroissante, l'ordre est renversé.9 sur 11
Yvan Monka - Académie de Strasbourg - www.maths-et-tiques.fr Méthode : Résoudre une inéquation avec la fonction inverseVidéo https://youtu.be/7K0171Zj5Rw
Résoudre l'inéquation suivante pour tout ��� strictement positif : 4 +2<5Correction
4 +2<5 4 <5-2 4 <3 1 3 4 1 4 3 4 3 4 3 ;+∞W3. Variations de la fonction racine carrée
Vidéo https://youtu.be/qJ-Iiz8TvZ4
Propriété : La fonction racine carrée est strictement croissante sur l'intervalle0;+∞
Démonstration au programme :
Vidéo https://youtu.be/1EUTIClDac4
On pose : ���
Soit ��� et ��� deux nombres réels positifs tels que ���<���. 1 0 31/4 0 3 /4 0 0 /4 0 /'0 /4 0 Or >0 et ���-���>0. Donc ��� >0
Donc ���
Ce qui prouve que f est croissante sur l'intervalle0;+∞
← On divise de part et d'autre par 4. ← On applique la propriété donnée plus haut.10 sur 11
Yvan Monka - Académie de Strasbourg - www.maths-et-tiques.fr Propriété : Si ��� et ��� sont deux nombres réels positifs, on a alors : En effet, la fonction racine carrée étant croissante, l'ordre est conservé.4. Variations de la fonction cube
Vidéo https://youtu.be/PRSDu_PgCZA
Propriété : La fonction cube est strictement croissante sur ℝ.Propriété : ���<������������é���������������������������à���
En effet, la fonction cube étant croissante, l'ordre est conservé. Méthode : Ordonner des nombres avec la fonction cubeVidéo https://youtu.be/8h8uAq0wH1A
Sans calculatrice, ranger les nombres suivants dans l'ordre croissant : 1 8 4 -5 Z 2 3 1 8Correction
On a :
1 8 1 2 1 2 =Z 1 2 -5 =(-5) 1 8 =Z- 1 2La fonction cube conserve l'ordre.
Donc, pour ranger dans l'ordre croissant les nombres : Z 1 2 4 (-5) Z 2 3 Z- 1 2 il suffit de ranger dans l'ordre croissant ces nombres sans l'exposant 3.Soit, à ranger :
1 2 4-5 2 3 1 2 Or :11 sur 11
Yvan Monka - Académie de Strasbourg - www.maths-et-tiques.fr -5<- 1 2 1 2 2 3 <4Donc :
-5[PDF] pilote brother dcp 7055w
[PDF] brother dcp-j172w driver
[PDF] plat typique des asturies
[PDF] technique de conservation des aliments les plus anciennes
[PDF] comment conserver les aliments au moyen age
[PDF] technique de conservation des aliments au fil du temps
[PDF] conservation du sel
[PDF] conservation des aliments dans l'antiquité
[PDF] conservation viande séchée
[PDF] culture de l'ail en afrique pdf
[PDF] vertue de l ail en pdf
[PDF] fiche technique ail
[PDF] les vertus de l'ail et de l'oignon pdf
[PDF] fiche technique ail pdf
