[PDF] CLASSE : 2nde DS 2G3 Vecteurs - Correction Durée approximative

View - Download CLASSE : 2nde DS 2G3 Vecteurs - Correction Durée approximative

Previous PDF

Next PDF

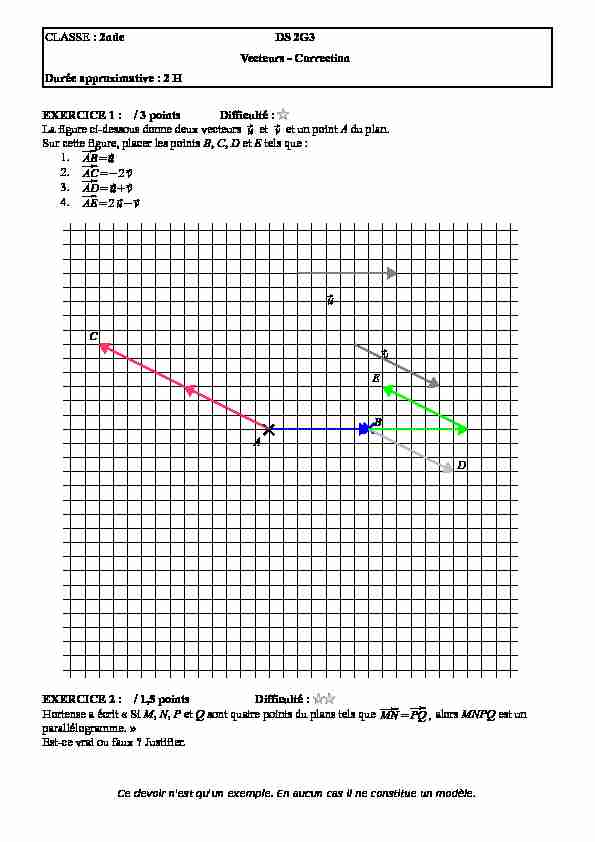
CLASSE : 2ndeDS 2G3

Vecteurs - Correction

Durée approximative : 2 H

EXERCICE 1 : / 3 points Difficulté :

La figure ci-dessous donne deux vecteurs ⃗u et ⃗v et un point A du plan. Sur cette figure, placer les points B, C, D et E tels que : 1. ⃗AB=⃗u 2. ⃗AC=-2⃗v3. ⃗AD=⃗u+⃗v4. ⃗AE=2⃗u-⃗v ⃗u ⃗v

EXERCICE 2 : / 1,5 points Difficulté :

Hortense a écrit " Si M, N, P et Q sont quatre points du plans tels que ⃗MN=⃗PQ,alors MNPQ est un parallélogramme. »

Est-ce vrai ou faux ? Justifier.

Ce devoir n'est qu'un exemple. En aucun cas il ne constitue un modèle.ABC DE

Correction :

C'est faux. Hortense a commis une erreur classique en inversant certains points. Un schéma représentant

deux vecteurs égaux, éventuellement réalisé à main levée, permet de se rendre compte de l'erreur :

La phrase correcte est " Si M, N, P et Q sont quatre points du plans tels que⃗MN=⃗PQ,alors MNQP est

un parallélogramme » car, par convention, on lit les noms des sommets en tournant autour du polygone.

EXERCICE 3 : / 2,5 points Difficulté :

Dans un repère orthonormé du plan, on considère les points A(-1; 3), B(2; 1), C(1 ; 0) et D(-2 ; 2).

1.Faire une figure en prenant comme unité graphique 1 cm.

2.Le quadrilatère ABCD est-il un parallélogramme ?

Correction :

Sur la figure, le quadrilatère ABCD semble être un parallélogramme. Pour s'en assurer, on peut calculer et

comparer les coordonnées des vecteurs ⃗AB et ⃗DC. ⃗AB a pour coordonnées :xB-xA=2-(-1)=3 et yB-yA=1-3=-2 donc ⃗AB(3;-2). ⃗DC a pour coordonnées :xC-xD=1-(-2)=3 et yC-yD=0-2=-2 donc ⃗DC(3;-2).

On constate que les vecteurs

⃗AB et ⃗DC ont les mêmes coordonnées donc ils sont égaux, ainsi ABCD est un parallélogramme.

Remarque : on peut également démontrer que les segments [AC] et [BD] se coupent en leur milieu, si on

connaît le formule donnant les coordonnées du milieu d'un segment en fonction des coordonnées des

extrémités de ce segment.

EXERCICE 4 : / 4 points Difficulté :

Dans un repère du plan, on considère les points M(-1; 4), N(-3 ; 3) et P(2 ; 2).

1.Calculer les coordonnées du vecteur

2⃗MN+⃗MP.

2.En déduire les coordonnées (

xD ; yD) du point D tel que ⃗MD=2⃗MN+⃗MP.

3.Soit E le point tel que

⃗NE=1

3⃗NP. Calculer les coordonnées du point E.

4.Montrer que les points M, E et D sont alignés.

Ce devoir n'est qu'un exemple. En aucun cas il ne constitue un modèle.MN PQ

Correction :

1.On peut commencer par calculer les coordonnées des vecteurs ⃗MN et ⃗MP :

Le vecteur

⃗MN a pour coordonnées : xN-xM=-3-(-1)=-2 et yN-yM=3-4=-1, soit ⃗MN(-2;-1) et ⃗MP : xP-xM:2-(-1)=3 et yP-yN=2-4=-2 soit ⃗MP(3;-2).

Le vecteur

2⃗MN+⃗MP a pour coordonnées : 2x⃗MN+x⃗MP=-4+3=-1 et

2y ⃗MN+y⃗MP=-2+(-2)=-4. Donc 2⃗MN+⃗MP a pour coordonnées (-1;-4).

2.Le vecteur

⃗MD a pour coordonnées (xD+1;yD-4). Or, deux vecteurs sont égaux si et seulement si leurs coordonnées sont égales. Ainsi, comme ⃗MD=2⃗MN+⃗MP, on a {xD+1=-1 yD-4=-4donc {xD=-2 yD=0. Les coordonnées du point D sont donc (-2;0).

3.Le vecteur

1

3⃗NP a pour coordonnées 1

3(xP-xN)=1

3(2-(-3))=5

3 et 1

3(yP-yN)=1

3(2-3)=-1

3 soit (1

3)⃗NP(5

3;-1 3).

Le vecteur

⃗NE a pour coordonnées (xE+3;yE-3). Or, deux vecteurs sont égaux si et seulement si leurs coordonnées sont égales. Ainsi, comme ⃗NE=(1

3)⃗NP, on a

{xE+3=5 3 yE-3=-1

3 d'où

{xE=5 3-9 3=-4 3 yE=-1 3+9 3=8

3. Les coordonnées du point E sont donc

(-4 3;8 3).

4.Pour montrer que les points M, E et D sont alignés, on peut par exemple montrer que les vecteurs

⃗ME et ⃗MD sont colinéaires : ⃗ME a pour coordonnées xE-xM=-4

3+1=-4

3+3 3=-1

3 et yE-yM=8

3-4=8 3-12 3=-4 3 soit ⃗ME(-1 3;-4

3). De même, le vecteur ⃗MD a pour coordonnées (-1;-4).

On s'aperçoit que

⃗MD=3⃗ME donc les vecteurs ⃗MD et ⃗ME sont colinéaires : les points M, D et E sont alignés.

EXERCICE 5 : / 2 points Difficulté :

Dans un repère du plan, soient les trois points S(-2 ; 5), T(2 ; 12) et V(38 ; 76). Ces points sont-ils

alignés ?

Correction :

Pour savoir si ces trois points sont alignés, on peut calculer les coordonnées de deux vecteurs construits

sur ces trois points et vérifier si ces vecteurs sont colinéaires, c'est-à-dire si les coordonnées de ces

vecteurs sont proportionnelles.

Le vecteur

⃗ST a pour coordonnées :xT-xS=2-(-2)=4 et yT-yS=12-5=7, soit ⃗ST(4;7).

Le vecteur

⃗TV a pour coordonnées :xV-xT=38-2=36 et yV-yT=76-12=64, soit ⃗TV(36 ;64).

Par calcul mental et connaissance de la table de 4 ou de 9, on reconnaît que 36 = 4×9, mais 7×9 est

différent de 64, donc les vecteurs ne sont pas colinéaires. Ce devoir n'est qu'un exemple. En aucun cas il ne constitue un modèle.

Une autre méthode plus systématique consiste à vérifier si les produits en croix sont égaux, dans le

tableau des coordonnées : 436
764
On constate que 4×64 est différent de 7×36.

Les vecteurs ⃗ST et ⃗TV ne sont pas colinéaires, donc les points S , T et V ne sont pas alignés.

Remarque : il est aussi possible de traiter cette question en déterminant une équation de la droite (SV) et

en testant si les coordonnées de T vérifient cette équation.

EXERCICE 6 : / 4 points Difficulté :

L'objectif de cet exercice est de démontrer le " théorème des milieux » à l'aide des vecteurs.

A, B et C sont trois points non alignés. Soient I le milieu du segment [AB], et J le milieu du segment [AC].

Le plan est muni du repère (A ; B ; C).

1.Quelles sont les coordonnées des points A, B et C dans le repère (A ; B ; C) ?

2.Quelles sont les coordonnées des points I et J dans ce même repère ?

3.Calculer les coordonnées des vecteurs

⃗BC et ⃗IJ.

4.Que peut-on en déduire pour la position relative des droites (IJ) et (BC) ?

5.Exprimer la distance IJ en fonction de la distance BC.

Correction :

1.Par définition, les trois points A, B et C, dans cet ordre, qui définissent le repère (A ; B ; C) ont

pour coordonnées A (0 ; 0), B (1 ; 0) et C (0 ; 1) .

2.Les coordonnées du milieu d'un segment sont égales aux moyennes des coordonnées des

extrémités de ce segment, donc I a pour coordonnées (xA+xB

2 ;yA+yB

2), soit I(1

2 ;0). De

même, J a pour coordonnées (xA+xC

2 ;yA+yC

2), soit J(0;1

2). 3. ⃗BC a pour coordonnées xC-xB=0-1 et yC-yB=1-0 soit ⃗BC(-1;1). D'autre part, ⃗IJ a pour coordonnées xJ-xI=0-1 2 et yJ-yI=1

2-0 donc ⃗IJ(-1

2 ;1 2).

4.Par calcul mental, on remarque que les coordonnées de

⃗IJ et ⃗BC sont proportionnelles, avec

⃗BC=2⃗IJ autrement dit ⃗BC et ⃗IJ sont colinéaires donc les droites ( IJ ) et ( BC ) sont parallèles .

5.Comme

⃗BC=2⃗IJ, on a l'égalité de distances : BC = 2 IJ .

Conclusion : nous avons démontré, en utilisant nos connaissances sur les vecteurs, le " théorème des

milieux » vus en collège :

Dans un triangle, le segment joignant les milieux de deux côtés est parallèle au troisième côté, et sa

longueur est la moitié de celle de ce troisième côté. Ce devoir n'est qu'un exemple. En aucun cas il ne constitue un modèle.

EXERCICE 7 : / 3 points Difficulté :

Voici un algorithme incomplet.

Entrées : xA, yA, xB, yB, xC, yC, xD, yD sont des coordonnées de points A, B, C, D.

Variables : xU, yU, xV, yV, xM, yM

Début

xU prend la valeur xB-xA yU prend la valeur yB-yA xV prend la valeur xD-xC yV prend la valeur yD-yC

Si ... et ...

alors afficher " ABDC est un parallélogramme » sinon afficher " ABDC n'est pas un parallélogramme » Fin

1.Compléter les pointillés de l'algorithme par des tests.

2.Modifier les dernières lignes de l'algorithme pour que celui-ci permette de tester si ABDC est un

trapèze ou un parallélogramme.

Correction :

Entrées : xA, yA, xB, yB, xC, yC, xD, yD sont des coordonnées de points A, B, C, D.

Variables : xU, yU, xV, yV, xM, yM

Début

xU prend la valeur xB-xA yU prend la valeur yB-yA xV prend la valeur xD-xC yV prend la valeur yD-yC

Si xU = xV et yU = yV

alors afficher " ABDC est un parallélogramme » sinon afficher " ABDC n'est pas un parallélogramme » Fin

Commentaire : on teste si les vecteurs ⃗AB et ⃗CD sont égaux (en comparant leurs coordonnées)

pour savoir si ABDC est un parallélogramme. 2. Entrées : xA, yA, xB, yB, xC, yC, xD, yD sont des coordonnées de points A, B, C, D.

Variables : xU, yU, xV, yV, xM, yM

Début

xU prend la valeur xB-xA yU prend la valeur yB-yA xV prend la valeur xD-xC yV prend la valeur yD-yC

Si xU × yV = xV × yU

alors afficher " ABDC est un trapèze» sinon afficher " ABDC n'est pas un trapèze» Fin

Commentaire : on teste si les vecteurs

⃗AB et ⃗CD sont colinéaires pour savoir si ABDC est un trapèze. On teste donc si les produits en croix sont égaux, dans le tableau des coordonnées : xUxV yUyV Ce devoir n'est qu'un exemple. En aucun cas il ne constitue un modèle.quotesdbs_dbs31.pdfusesText_37

[PDF] exercices corrigés de stéréoisomérie

[PDF] exercices corrigés en stéreochimie

[PDF] projection de newman exercices corrigés

[PDF] cisco 8851 mode d'emploi

[PDF] comment configurer un telephone ip

[PDF] configuration telephone ip cisco pdf

[PDF] configuration telephone ip packet tracer

[PDF] confiture mirabelle

[PDF] confiture pdf

[PDF] recette confiture de mangues facile

[PDF] chimie des confitures

[PDF] tableau pectine fruit

[PDF] ph confiture

[PDF] toute action collective constitue-t-elle un mouvement social ?

[PDF] en quoi les conflits sociaux peuvent-ils être considérés comme une forme de pathologie ec1