 Correction TP de programmation no4
Correction TP de programmation no4
Écrire une procédure somme qui calcule la somme de deux nombres complexes. Écrire une procédure inverse qui retourne l'inverse d'un nombre complexe.
 Conjugué dun nombre complexe - Un doc de Jérôme ONILLON
Conjugué dun nombre complexe - Un doc de Jérôme ONILLON
Propriété : le conjugué de l'inverse est égal à l'inverse du conjugué. Le conjugué d'un quotient est égal au quotient des conjugués. 1. 1 z z.
 NOMBRES COMPLEXES – Chapitre 2/4
NOMBRES COMPLEXES – Chapitre 2/4
Le point (3 ; 2) a pour affixe le nombre complexe =3+2 . De même le vecteur AA? a pour Donc l'inverse a pour module 1 et appartient donc à .
 Nombres complexes (partie 1) - Editions Ellipses
Nombres complexes (partie 1) - Editions Ellipses
Ensemble C des nombres complexes. Partie réelle et partie imaginaire. Opérations. > Conjugaison. Propriétés algébriques. > Inverse d'un nombre complexe non
 Nombres complexes (partie 1)
Nombres complexes (partie 1)
Ensemble C des nombres complexes. Partie réelle et partie imaginaire. Opérations. > Conjugaison. Propriétés algébriques. > Inverse d'un nombre complexe non
 Nombres complexes. Représentation géométrique. Notation
Nombres complexes. Représentation géométrique. Notation
Le module de l'inverse d'un nombre complexe non nul est l'inverse du module de ce nombre complexe. z ?C* ?1 z?= 1. ?z?. Démonstration :.
 Exercices : nombre complexe - Calcul Corrigés en vidéo et le cours
Exercices : nombre complexe - Calcul Corrigés en vidéo et le cours
Inverse d'un nombre complexe. Déterminer les inverses des nombres suivants. On donnera le résultat sous forme algébrique. a) 2 ? i b) i. 2 ? 3i c
 Les nombres complexes - Division des nombres complexes
Les nombres complexes - Division des nombres complexes
La division d'un nombre complexe a + i b par un nombre complexe c + i d donne un nouveau nombre complexe x + i y : a + i b c + i d. = x + i y. • L'inverse
 Chapitre 2 - Les nombres complexes I : première approche et lien
Chapitre 2 - Les nombres complexes I : première approche et lien
Manipuler algébriquement des nombres complexes à partir de leur forme algébrique. Calculer le conjugué le module et l'inverse d'un nombre complexe.
 NOMBRES COMPLEXES
NOMBRES COMPLEXES
I.2 L'ensemble des nombres complexes . II.5 Inverse d'un complexe . ... Deux nombres complexes sont égaux si et seulement si ils ont même partie réelle ...
 [PDF] NOMBRES COMPLEXES
[PDF] NOMBRES COMPLEXES
le module est l'inverse du module de z ; • l'argument est l'opposé de l'argument de z Ce résultat se traduit par la formule 1 ??cis ?( ) = 1 ?
 [PDF] Inversion complexe et cocyclicité - Université de Rennes
[PDF] Inversion complexe et cocyclicité - Université de Rennes
Inversion complexe et cocyclicité Jean-Marie Lion Université de Rennes 1 Br`eve introduction aux nombres complexes L'addition et la multiplication dans
 [PDF] 1 Corps des nombres complexes
[PDF] 1 Corps des nombres complexes
C'est le seul nombre complexe vérifiant pour tout z ? C : z(1 + 0i)=(1+0i)z = z Tout élement z ? C distinct de 0 admet un symétrique z/ appelé inverse
 [PDF] NOMBRES COMPLEXES - Nathalie Daval - Free
[PDF] NOMBRES COMPLEXES - Nathalie Daval - Free
I 2 L'ensemble des nombres complexes II 5 Inverse d'un complexe Deux nombres complexes sont égaux si et seulement si ils ont même partie réelle
 [PDF] Nombres complexes - Exo7 - Cours de mathématiques
[PDF] Nombres complexes - Exo7 - Cours de mathématiques
L'inverse de z noté 1 z est donc z = 1 z = a a2 + b2 + i ?b a2 + b2 = a ? i b a2 + b2 • La division : z z est le nombre complexe z × 1
 [PDF] Fiche 6 : Nombres complexes - Studyrama
[PDF] Fiche 6 : Nombres complexes - Studyrama
Inverse d'un nombre complexe Soit z x iy = + un complexe non nul avec x et y réels Pour déterminer partie réelle et partie imaginaire de
 [PDF] NOMBRES COMPLEXES (Partie 2) - maths et tiques
[PDF] NOMBRES COMPLEXES (Partie 2) - maths et tiques
I Module et argument d'un nombre complexe 1) Module Définition : Soit un nombre complexe z = a + ib On appelle module de z le nombre réel positif
 [PDF] Nombres complexes - Forme algébrique - Parfenoff org
[PDF] Nombres complexes - Forme algébrique - Parfenoff org
Cette écriture est dite forme algébrique du nombre complexe c) Définition : inverse d'un nombre complexe Si le nombre complexe est non nul alors :
 [PDF] Nombres complexes - Licence de mathématiques Lyon 1
[PDF] Nombres complexes - Licence de mathématiques Lyon 1
en pratique un nombre complexe z poss`ede deux représentations : (viii) tout élément non nul admet un inverse : pour tout a de K différent de 0
 [PDF] Nombres complexes : forme algébrique
[PDF] Nombres complexes : forme algébrique
II 5 Inverse V Forme trigonométrique d'un nombre complexe troisiéme et du quatriéme degré et l'invention des nombres complexes
Quel est l'inverse d'un nombre complexe ?
Opposé d'un nombre complexe
L'opposé de z est le nombre (-z) tel que z + (-z) = 0.Comment calculer l'opposé d'un nombre complexe ?
L'opposé du nombre complexe a+bi est le nombre complexe ?a?bi. L'inverse du nombre complexe a+bi est le nombre complexe aa2+b2?ba2+b2i.Comment déterminer l'argument de z ?
On peut alors calculer l'argument de �� dans les différents quadrants comme suit :
1Quadrant 1 : a r g ( �� ) = ��2Quadrant 2 : a r g ( �� ) = �� ? ��3Quadrant 3 : a r g ( �� ) = �� ? ��4Quadrant 4 : a r g ( �� ) = ? ��- À tout nombre complexe z = a + i b ? C est associé le point M du plan de coordonnées appelé image de et noté . A tout point M du plan de coordonnées est associé le complexe z M = a + i b appelé affixe du point M.
 1
1 NOMBRES COMPLEXES - Chapitre 2/4
Tout le cours en vidéo : https://youtu.be/ABo2m52oEYw Dans tout le chapitre, on munit le plan d'un repère orthonormé direct Partie 1 : Représentation dans le plan complexe1) Définitions
Définitions : ��� et ��� sont deux nombres réels.- À tout nombre complexe ���=���+������, on associe son image, le point ��� de coordonnées
et tout vecteur ���������⃗ de coordonnées - À tout point ��� et à tout vecteur���������⃗ , on associe le nombre complexe���=���+������ appelé affixe du point ��� et affixe du vecteur ���������⃗.
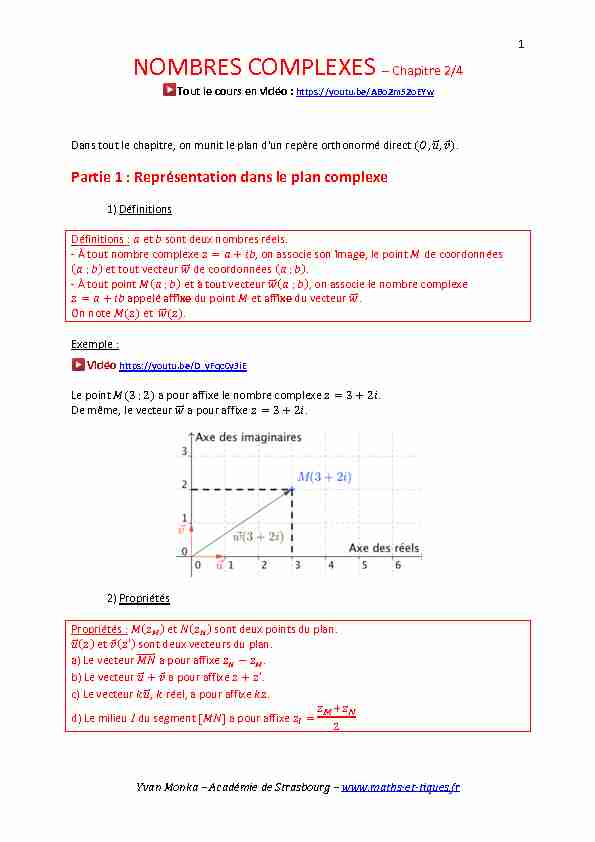
On note ���(���) et ���������⃗(���).Exemple :
Vidéo https://youtu.be/D_yFqcCy3iE
Le point ���(3;2) a pour affixe le nombre complexe ���=3+2���. De même, le vecteur ���������⃗ a pour affixe ���=3+2���.2) Propriétés
Propriétés : ���
et ��� sont deux points du plan. et ���⃗ sont deux vecteurs du plan. a) Le vecteur ������ a pour affixe ��� b) Le vecteur ������⃗+���⃗ a pour affixe ���+���′. c) Le vecteur ���������⃗, ��� réel, a pour affixe ������. d) Le milieu ��� du segment [������] a pour affixe ��� 2Démonstrations :
a) On pose : ��� et ���Le vecteur ������
a pour coordonnées donc son affixe est égal à : b) c) et d) : Démonstrations analogues en passant par les coordonnées des vecteurs.Autres exemples :
Méthode : Utiliser l'affixe d'un point en géométrieVidéo https://youtu.be/m9yM6kw1ZzU
On considère les points ���(-2+3���), ���(2+4���), ���(5+3���), ���(1+2���) et ���(-7).
a) Démontrer que le quadrilatère ������������ est un parallélogramme. Calculer l'affixe de son
centre. b) Les points ���, ��� et ��� sont-ils alignés ?Correction
a) - On va démontrer que les vecteurs ������ et ������ sont égaux.Affixe de ������
=2+4���- -2+3��� =4+���Affixe de ������
=5+3���-1+2���
=4+���Donc ������
et donc ������������ est un parallélogramme. - Le centre du parallélogramme est le milieu ��� du segment [������]. Son affixe est : 2 -2+3���+5+3��� 23+6���
2 3 2 +3��� b) On va démontrer que les vecteurs ������ et ������ sont colinéaires. 3Affixe de ������
=4+���Affixe de ������
=-7-1+2���
=-8-2���.Donc : ���
=-2��� et donc ������ =-2������Les vecteurs ������
et ������ sont colinéaires et donc les points ���, ��� et ��� sont alignés.3) Image d'un conjugué
Remarque :
Les images ��� et ���' de ��� et ���̅ sont symétriques par rapport à l'axe des réels. Partie 2 : Module et argument d'un nombre complexe1) Module
Définition : Soit un nombre complexe ���=���+������. On appelle module de ���, le nombre réel positif, noté , égal à ��� est un point d'affixe ���.Alors le module de ��� est égal à la
distance ������. Propriétés : Soit ��� un nombre complexe. a) =������̅ b) c)Démonstrations (dont a) au programme) :
a) ������̅= b) N c) N 4 Propriétés : Soit ��� et ���′ deux nombres complexes non nuls et ��� entier naturel non nul.Produit
Puissance
Inverse
1 1Quotient
Q Q=Démonstrations au programme :
- Module d'un produit : On pose ���=���������(���) et ���′=���������(���′). cos���+���sin��� cos���′+���sin���′ Z cos +���sinDonc le module de ������
est - Module d'une puissance :On procède par récurrence.
• Initialisation pour ���=2 : , d'après la propriété du produit. • Hérédité : - Hypothèse de récurrence : Supposons qu'il existe un entier ���>1 tel que la propriété soit vraie : - Démontrons que : La propriété est vraie au rang ���+1 : ./0 ./0 ./0 , d'après la propriété du produit. , par hypothèse de récurrence. ./0 • Conclusion :La propriété est vraie pour ���=1 et héréditaire à partir de ce rang. D'après le principe de
récurrence, elle est vraie pour tout entier naturel ���, soit : Méthode : Calculer le module d'un nombre complexeVidéo https://youtu.be/Hu0jjS5O2u4
Vidéo https://youtu.be/i85d2fKv34w
Calculer : a)
3-2���
b) -3��� c) `2+���` d)
Correction
a)3-2���
N 3 -213 b)
-3��� -3��� -3 =3×1=3 c) `2+���`=
a 2 +1 3 5 d) 3 2 = 12) Argument
Définition : Soit un point ��� d'affixe ��� non nulle.On appelle argument de ���, noté ���������(���) une mesure, en radians, de l'angle Z������⃗;������
Remarques :
- Un nombre complexe non nul possède une infinité d'arguments de la forme ��������� +2������,On notera ���������
modulo 2��� ou ���������2���
- 0 n'a pas d'argument car dans ce cas l'angle Z������⃗;������ [ n'est pas défini.Exemple :
Soit ���=3+3���.
Alors3+3���
3 +3 18=3 2 42���
Propriétés : Soit ��� un nombre complexe non nul. a) ��� est un nombre réel ⟺��������� =0 b) ��� est un imaginaire pur ⟺��������� c) ��������� d)��������� 6Démonstrations :
a) Le point M d'affixe ��� appartient à l'axe des réels. b) Le point M d'affixe ��� appartient à l'axe des imaginaires. c) d) Ses résultats se déduisent par symétrie. Méthode : Déterminer géométriquement un argumentVidéo https://youtu.be/NX3pzPL2gwc
a) Déterminer un argument de chaque affixe des points A, B et C. b) Placer les points D et E d'affixes respectives ��� et ��� telles que : =2 et arg 32���
=3 et arg3���
42���
Correction
a) arg 42���
arg 32���
arg2���
b) Le point D appartient au cercle de rayon 2 car 2.Le point E appartient au cercle de rayon 3 car
=3. 43���4-2���3
7 Propriétés : Soit ��� et ���′ deux nombres complexes non nuls et ��� entier naturel non nul.Produit
Puissance
Inverse
���������j 1 k=-���������(���)Quotient ���������l
Partie 3 : Forme trigonométrique d'un nombre complexe1) Définition
Propriété : Soit ���=���+������ un nombre complexe non nul. On pose : ���=���������(���)
On a alors : ���=
cos��� et ���= sin���. En effet, en considérant le triangle rectangle, on a : cos���= sin���=Définition : On appelle forme trigonométrique d'un nombre complexe ��� non nul l'écriture
cos���+���sin��� avec ���=���������(���). Méthode : Passer de la forme trigonométrique à la forme algébrique et réciproquementVidéo https://youtu.be/kmb3-hNiBq8
Vidéo https://youtu.be/zIbpXlgISc4
Vidéo https://youtu.be/RqRQ2m-9Uhw
1) Écrire les nombres complexes suivants sous forme algébrique :
0 =33l���������l-
6 m+������������l- 6 mm2) Écrire les nombres complexes suivants sous forme trigonométrique :
2 =-5������)��� 33+���
8Correction
1)���)���
0 =3 =3 -1+���×0 =-3.3lcosl-
6 m+���sinl- 6 mm=3���
3 2 +���×j- 1 2 kr= 3 2 3 22)���)
2 -5��� =5 Géométriquement (cercle trigo), on peut affirmer que : arg 2 42���
Donc : ���
2 =5lcosl- 4 m+���sinl- 4 mm. ���) - On commence par calculer le module de ��� 3 3 a 3 +1 3+1=2 - En calculant , on peut identifier plus facilement la partie réelle de ��� 3 et sa partie imaginaire : 3 3 3 2 1 2On cherche donc un argument ��� de ���
3 tel que : cos���= 3 2 ������sin���= 1 2 6 convient, en effet : cos 6 3 2 etsin 6 1 2On a ainsi :
3 3 =cos 6 +���sin 6Et donc :
3 3 lcos 6 +���sin 6 m=2lcos 6 +���sin 6 m. Partie 4 : Ensemble ��� des nombres complexes de module 11) Cercle trigonométrique
L'ensemble des points du plan complexe
dont l'affixe appartient au cercle de centre O et de rayon 1 est noté ���. Ce cercle s'appelle le cercle trigonométrique. Propriété : Soit ���=���+������ un nombre complexe appartenant à ���.On a alors ���
=1. 92) Stabilité de ���
Méthode : Prouver que ��� est stable par produit et passage à l'inverseVidéo https://youtu.be/XTNKoNfFopw
Soit ��� et ���' deux nombres complexes appartenant à ���.Démontrer que ������' et
2 appartiennent à ���.Correction
=1×1 car ��� et ���' appartiennent à ���. =1 Donc le produit ������' a pour module 1 et appartient donc à ���.On dit que ��� est stable par produit.
2 2 2 2 car ��� appartient à ���. =1Donc l'inverse
2 a pour module 1 et appartient donc à ���. On dit que ��� est stable par passage à l'inverse.quotesdbs_dbs29.pdfusesText_35[PDF] conjuguer les verbes entre parenthèses au passé composé
[PDF] conjuguer les verbes entre parenthèses au temps qui convient
[PDF] mets les verbes entre parenthèses au présent
[PDF] tout les temps de l'indicatif
[PDF] pluperfect en anglais
[PDF] preterit be ing ou preterit simple
[PDF] preterit have
[PDF] preterit be ing equivalent francais
[PDF] pluperfect be ing
[PDF] preterit be anglais
[PDF] prétérit continu
[PDF] exercices temps verbaux français
[PDF] passé présent futur ce2 pdf
[PDF] exercice passé présent futur ce2 a imprimer
