[PDF] [PDF] Feuille dexercices n?8 : corrigé - Normale Sup

View - Download [PDF] Feuille dexercices n?8 : corrigé - Normale Sup

Previous PDF

Next PDF

Feuille d"exercices n°8 : corrigé

ECE3 Lycée Carnot

13 décembre 2011

Exercice 1 (**)

Une petite transformation est nécessaire pour ramener cette série à un calcul connu, en l"oc-

curence celui de la somme d"une série géométrique dérivée seconde : N X n=0n

2xn=NX

n=0n(n1)xn+NX n=0nx n=x2NX n=0n(n1)xn2+xNX n=0nx n1 La série est donc convergente si (et seulement si)jxj<1, et sa somme vaut en appliquant les formules du cours +1X n=0n

2xn=x22(1x)3+x1(1x)2=2x2+x(1x)(1x)3=x2+x(1x)3=x(1 +x)(1x)3

NX n=0n13 n=NX n=0n3 nNX n=013 n=13 N X n=0n13 n1 NX n=013 n. La série est donc convergente, de somme +1X n=0n 213
n=13 1(113 )21113 =13 94
32
=34 32
=34 NX n=2n(n1)xnn!=x2NX n=2x n2(n2)!=x2N2X n=0x nn!, qui converge versx2ex(note : on a commencé la somme de départ àn= 2car les termes obtenus pourn= 0etn= 1seraient de toute façon nuls). NX n=0n

28nn!=NX

n=0n(n1)8nn!+NX n=0n8nn!=NX n=28 n(n2)!+NX n=18 n(n1)!= 82NX n=28 n2(n2)!+ 8 NX n=18 n1(n1)!= 82N2X n=08 nn!+ 8N1X n=08 nn!, qui converge vers64e8+ 8e8= 72e8. NX n=04n2+ 5n5 n= 4NX n=0n 25
n+NX n=0n5 n1qui converge vers415 (15 + 1)(115 )3+1(115 )2(en utilisant le résultat du premier calcul de l"exercice pour la première somme)=2425 534
3+524

2=3016

+2516
5516

En constatant que8n>2,2n2n

31>2n2n

3=2n , on voit que notre série est une série à termes

positifs dont le terme général est minoré par celui d"une série divergente, donc elle diverge.

1 On utilise encore une fois le résultat du premier calcul de l"exercice : +1X n=0(1)nn23 n=13 (13 + 1)(1 + 13 )3=29 334
3=664 =332 Ici, on a une série exponentielle, c"est du cours!+1X n=04(1)nn!= 4e1=4e NX n=0n3

2n+1=13

3N X n=0n3

2n2=127

N X n=0n9 n1On reconnait une série géométrique dérivée, qui converge vers 127
1(119 )2=127 8164
=364 NX n=0n+ 72 nn!=NX n=1n2 nn!+NX n=072 nn!=12 N1X n=012 nn!+NX n=072 nn!, qui converge vers12 e12 +7e12
=152 e12 On reconnait une somme télescopique dans la somme partielle :nX k=1lnk+ 1k =nX k=1ln(k+

1)lnk= ln(n+ 1)ln1. Comme cette expression ne converge pas quandntend vers+1,

la série est divergente. Même principe avec un télescopage plus complexe :nX k=1ln(k+ 1)2k(k+ 2) =nX k=12ln(k+1)lnk ln(k+2) = 2n+1X k=2lnknX k=1lnkn+2X k=3lnk= 2ln2+2ln(n+1)ln1ln2ln(n+1)ln(n+2) = ln2+ln(n+1)ln(n+2) = ln2+lnn+ 1n+ 2. Cette expression converge quandntend vers+1, donc la série est convergente, et +1X k=1ln(n+ 1)2n(n+ 2) = ln2.

Exercice 2 (**)

Le plus simple pour déterminer la nature de la série est de chercher à calculer sa somme. Suivant

les conseils de l"énoncé, on calcule an +bn+ 1+cn+ 1=a(n+ 1)(n+ 2) +bn(n+ 2) +cn(n+ 1)n(n+ 1)(n+ 2)=

a(n2+ 3n+ 2) +b(n2+ 2n) +c(n2+n)n(n+ 1)(n+ 2)=(a+b+c)n2+ (3a+ 2b+c)n+ 2an(n+ 1)(n+ 2). par identification

des coefficients, on doit avoira+b+c= 0,3a+ 2b+c= 0et2a= 1, soita=12 . Les deux autres

équations donnentb+c=12

, soitc=b12 , puis2b+c=32 , soitb12 =32 , dont on déduit b=1, puisc=12 . On a donc finalement1n(n+ 1)(n+ 2)=12n1n+ 1+12(n+ 2). On peut faire un joli télescopage à partir de ceci : nX k=112n1n+ 112(n+ 2)=12 n X k=11n n+1X k=21n 12 n+2X k=31n =12 +14 12

1n+ 1+12(n+ 1)+12(n+ 2)=14

12(n+ 1)+12(n+ 2). La somme partielle

ayant une limite, la série converge, et on a +1X n=11n(n+ 1)(n+ 2)=14 2

Exercice 3 (**)

Le principe est le même que dans l"exercice précédent :

14n21=1(2n1)(2n+ 1)=a2n1+

b2n+ 1, avecaetbvérifianta(2n+ 1) +b(2n1) = 1, soitn(2a+ 2b) +ab= 1. On obtient facilementa=b, puisa=12 etb=12 , d"où14n21=12(2n1)12(2n+ 1). On a donc n X k=114k21=12 n X k=112k112 k=nX k=112k+ 1=12

12(2n+ 1)(c"est une somme télescopique simple).

La somme partielle converge, donc la série est convergente, et +1X n=114n21=12

Exercice 4 (**)

1. On montre par une récurrence facile que8n2N,un>0. En effet, c"est vrai pouru0, et si on

le suppose vrai pourun, commeeun>0, on aura bienun+1=eunun>0. De plus, comme u n>0, on aeun<1, et donceunun< un. Autrement dit, la suite(un)est décroissante. Comme elle est minorée par0, elle converge vers une certaine limitel. On en déduit queeunun tend verslel, mais aussi verslpuisque cette expression est égale àun+1. On en déduit que l=lel, ce qui se produit sil= 0ou siel= 1, ce qui ne laisse que la possibilitél= 0. La suite(un)converge donc vers0.

2. On remarque quevn+1= ln(un+1) = ln(eunun) =un+lnun=vnun, ce qu"on peut aussi

écrireun=vnvn+1. On en déduit queSn=nX

k=0u k=nX k=0(vkvk+1) =v0vn+1(il y a télescopage).

3. Commeuntend vers0, la suitevndiverge vers1quandntend vers+1, et la série(Sn)

diverge donc vers+1.

Exercice 5 (**)

On aS2nSn=k=2nX

k=11k k=nX k=11k =k=2nX k=n+11k . Chacun desntermes de cette dernière somme étant plus grand que

12n, la somme est plus grande quen12n=12

. Or, si la série harmonique convergait vers une certaine sommeS, on devrait avoirlimn!+1S2n= limn!+1Sn=S, donclimn!+1S2nSn= 0.

Ce n"est manifestement pas le cas, donc la série harmonique ne converge pas (un petit raisonnement

par l"absurde).

Exercice 6 (***)

1. On peut commencer par constater assez aisément que la suite(un)est décroissante puisque

u n+1un=u2n60. Cela donne bien envie de tenter de la minorer, par exemple par0.

Prouvons via une petite récurrence que tous les termes de la suite appartiennent à l"intervalle

[0;1]. C"est vrai pouru0par hypothèse. Supposons donc06un61, on a alors également

061un61, donc06un(1un)61. Or,un(1un) =unu2n=un+1. Cette constatation

achève la récurrence. La suite(un)étant décroissante minorée, elle converge. Commeun+1=unu2n, on en déduit en prenant la limite de chaque côté quel=ll2, soitl2= 0, ce qui n"est possible que si 3 l= 0. On peut en déduire que la suite(un)converge vers0.

2. En revenant à la relation de récurrence, on constate queu2n=unun+1, d"oùk=nX

k=0u

2k=k=nX

k=0u k u k+1=u0un+1(par télescopage). D"après la question précédente,limn!+1u0un+1=u0, donc la série de terme généralu2nconverge versu0.

3. La somme partielle va également être télescopique :

k=nX k=0lnuk+1u k =k=nX k=0ln(uk+1)ln(uk) = ln(un+1)ln(u0). Or, toujours en utilisant notre connaissance de la limite de(un), on a limn!+1ln(un+1) =1, ce qui signifie que la série considérére diverge.

4. En reprenant la relation de récurrence définissant la suite, on constate quelnun+1u

n ln unu2nu n = ln(1un) unpuisqueunest une suite qui converge vers0. Deux séries

de terme général équivalent ayant même nature (oui, je sais, dans le cours on a mis des séries

à termes positifs, et celles-là sont à terme négatif, mais il suffit d"appliquer le théorème à leurs

opposés pour que ça marche; ce qui est important c"est que les séries soient de signe constant),Xu

ndiverge.

Exercice 7 (*)

1k 2k1k

2, terme général d"une série convergente, doncX1k

2kconverge.

1e k+ek61e k, terme général d"une série géométrique convergente, donc la série à termes positifs X1e k+ekconverge. 1k

3+ 2k1k

3, terme général d"une série de Riemann convergente, donc la série à termes positifs

X1k

3+ 2kconverge.

lnn2+n42n4tend versln12 quandntend vers+1, donc la série diverge. rn+ 2n

35n+ 1r1

n 21n
, terme général d"une série divergente, donc la série diverge. lnn3 n=23 n lnn2 n. La deuxième fraction tendant rapidement vers0(par croissance com- parée), on aura certainement (à partir d"un certain rang) lnn3 n623 n , terme général d"une série géométrique convergeante, donc la série converge.

Exercice 8 (**)

La série de terme général

1(2k+ 1)2converge car son terme général est équivalent à14k2. De

même pour la série de terme général

1(2k+ 2)2. On peut donc écrire que la série de terme général

1(2k+ 2)2+1(2k+ 1)2converge, et que+1X

k=01(2k+ 1)2+1(2k+ 2)2=+1X k=01(2k+ 1)2++1X k=01(2k+ 2)2. Or, la somme de gauche n"est autre que la somme des inverses des carrés de tous les entiers (on a 4 juste séparé entiers pairs et impairs) qui vaut 26
. Quant à la deuxième somme à droite, elle vaut +1X k=014(k+ 1)2=14 +1X k=01(k+ 1)2=14 +1X k=11k 2=14 26
. Conclusion :+1X k=01(2k+ 1)2=26 14 26
34
26
=28

Problème

1 Un exemple

1. C"est une récurrence double facile :u1etu2sont des entiers, et en supposant queunetun+1

sont tous les deux entiers, la relation de récurrence implique queun+22Z, ce qui prouve l"hérédité.

2. La suite est récurrente linéaire double, d"équation caractéristiquex25x+6 = 0. Cette dernière

a pour discriminant = 2524 = 1, et admet deux racinesr=5 + 12 = 3ets=512 = 2. On en déduit queun=3n+2n, oùet, au vu des valeurs initiales, vérifient3+2= 2 et9+ 4= 3. En soustrayant le double de la première équation à la deuxième, on obtient

3=1, soit=13

, puis=232 =32 . Conclusion :8n>1,un= 32n13n1.

3. Les sommes partielles de la série sont données par

k=nX k=1u kk!=32 k=nX k=12 kk!13 k=nX k=13 kk!. Chacune de

ces deux séries est convergente (séries exponentielles, au manque du premier terme près), donc

la série étudiée également et sa somme vaut +1X n=1u nn!=32 (e21)13 (e31) =32 e2e33 76

4. Si l"équation caractéristique admet deux racines distinctes (discriminant strictement positif), la

suite peut se mettre sous la formern+sn, et les sommes partielles de la série étudiée seront

sommes de deux séries exponentielles convergentes. S"il y a une racine double, on peut mettre u nsous la formeun= (+n)rn, et cette fois les sommes partielles s"écrirontk=nX k=1r kk!+ s k=nX k=1s k1(k1)!, qui est encore une fois une somme de deux séries exponentielles convergentes.

2 Série exponentielle

1. Cela se fait très bien par récurrence. Pourn= 4,24= 16et4! = 24, donc l"inégalité est

vérifiée. Si on suppose que, pour un certain entier supérieur ou égal à4,2n6n!, alors2n+1=

22n62n!6(n+ 1)n! = (n+ 1)!, ce qui prouve l"hérédité et achève la récurrence.

2. Pour tout les indices de la somme, au vu de la question précédente, on aura

1k!612

k, donc k=nX k=41k!6k=nX k=412 k, somme géométrique égale à12

4k=n4X

k=012 k=12 4112
n3112 =18 112
n3 618

3. La série exponentielle est une série à termes positifs, majorée au vu de ce qui précède par

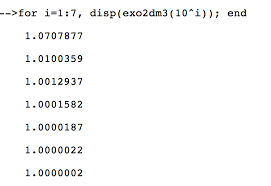
10! +11! +12! +13! +18 . Elle converge donc, et sa limitelvérifie certainement1 + 1 +12 +16 6 l61 + 1 +12 +16 +18 , soit83

6l66427

4. PROGRAM expo;

USES wincrt;

5

VAR s : real; i,f,n : integer;

BEGIN

WriteLn("Choisissez un entier n");

ReadLn(n);

s := 1; f := 1;

FOR i := 1 TO n DO

BEGIN f := f*i;quotesdbs_dbs45.pdfusesText_45

[PDF] somme changement d'indice

[PDF] somme télescopique exercice corrigé

[PDF] série téléscopique exercice

[PDF] somme télescopique suite

[PDF] somme telescopique convergence

[PDF] somme théologique iii

[PDF] saint thomas d aquin wikipedia

[PDF] somme théologique saint thomas pdf

[PDF] le chat et les pigeons pdf

[PDF] obligation d être prof principal

[PDF] décret no 93-55 du 15 janvier 1993

[PDF] bo n°5 du 4 février 1993

[PDF] je ne vois dans tout animal qu'une machine ingénieuse these

[PDF] explication de texte philosophie rousseau discours sur l origine

[PDF] différents aspects du travail