Feuille dexercices n˚8 : corrigé
13 déc. 2011 1. 2 . • On reconnait une somme télescopique dans la somme partielle : n. ∑ k=1 ln. (k + 1 k. ) = n. ∑ k=1 ln(k +. 1) − lnk = ln(n + 1) − ln ...
Exercice. Convergence de ∑ ln(1 − 1 k2 ) et valeur de la somme de
Donc ∑(an+1 −an) converge absolument par règle de comparaison. La série est téléscopique donc (an) converge et il existe γ tq an = γ + o(1).
Séries
(somme télescopique). Si la série de terme général un converge alors limn→+∞ un = 0 et donc 0 < un. ∼ n→+∞ ln(1+un). Donc la série de terme général ln(1
Somme téléscopique À laide dun téléscopage
25 sept. 2021 — On mobilisera les propriétés opératoires de la fonction logarithme pour cela. Éléments de correction. On a tout d'abord que : ∀k ∈ 2; n ln.
Devoir Maison n 3
On va majorer chaque terme de la somme par ln(k)−ln(k −1). Cependant l On reconnaîtra ensuite une somme télescopique. vn. = 1+ n. ∑ k=2. 1 k. ≤ 1 + n.
Sommes et Produits 1 Sommes
S3 = ln 2 + ln 4 + ln 6 + + ln 12. S4 = 1 − 2+3 − 4 + ... − 102 + 103 ... On parle de somme télescopique lorsque le terme général est la différence ...
Calculs de sommes et de produits finis
10 août 2023 Sommes téléscopiques. Proposition 4
Les symboles somme et produit - Lycée dAdultes
27 fév. 2017 k. • On utilise une somme télescopique : Sn − xSn = n. C k=p x k ... ln ak. 2.3 Produits télescopiques. Théorème 7 : Produits télescopiques.
Feuille dexercices no 5 - Sommes et produits
Des sommes télescopiques. Calculer les sommes suivantes : 1. (#) A = n. ∑ k=1 ln(k + 1) − ln k = ln(n + 1) − ln(1) = ln(n + 1). 19. n. ∑ k=0. 1. (k + 2)(k ...
Feuille dexercices n?8 : corrigé
13 déc. 2011 On reconnait une somme télescopique dans la somme partielle : ... ln 2. Exercice 2 (**). Le plus simple pour déterminer la nature de la ...
Exercice. Convergence de ? ln(1 ? 1 k2 ) et valeur de la somme de
Donc ?(an+1 ?an) converge absolument par règle de comparaison. La série est téléscopique donc (an) converge et il existe ? tq an = ? + o(1).
Séries
(somme télescopique). Si la série de terme général un converge alors limn?+? un = 0 et donc 0 < un. ? n?+? ln(1+un). Donc la série.
Les symboles somme et produit - Lycée dAdultes
27 févr. 2017 entiers naturels n et p tels que p ? n on définit la somme suivante par ... ln ( n n k=p ak) = n. C k=p ln ak. 2.3 Produits télescopiques.
Séries
En effet elle peut être écrite comme somme télescopique
Calculs de sommes et de produits finis
13 sept. 2021 Application
Séries
16 mars 2020 ln(n). = 1. Par théorème d'encadrement on trouve ainsi que lim n?+?. Sn ln(n) ... n+1
Sommes et produits de nombres
ln( k2. (k ? 1)(k + 1)) . Exercice 6 : Écrire à l'aide de factorielles les expressions suivantes : (a) n.
Feuille dexercices n?21 : corrigé
5 juin 2014 u0 ? un+1 = u0 donc la série de terme général u2 n converge vers u0. 3. La somme partielle va également être télescopique : k=n. ? k=0 ln.
Compléments sur les suites Suites adjacentes - Correction - Lycée d
27 févr. 2017 Comme la dernière somme est télescopique on a un ? ln(n + 1) ? ln 1 ? un ? ln(n + 1) or lim n?+? ln(n + 1)=+?
[PDF] [PDF] Séries - Exo7 - Cours de mathématiques
Une somme télescopique est une série de la forme ? k?0 (ak+1 ? ak) Cette série est convergente si et seulement si l := limk?+? ak existe et dans ce
[PDF] Feuille dexercices n?8 : corrigé - Normale Sup
13 déc 2011 · On reconnait une somme télescopique dans la somme partielle : n ? k=1 ln (k + 1 k ) = n ? k=1 ln(k + 1) ? lnk = ln(n + 1) ? ln 1
[PDF] Devoir Maison n?3
On reconnaîtra ensuite une somme télescopique vn = 1+ n ? k=2 1 k ? 1 + n ? k=2 (ln(k) ? ln(k ? 1)) ? 1 + ln(n) ? ln(2 ? 1) ? 1 + ln(n)
[PDF] Les symboles somme et produit - Lycée dAdultes
27 fév 2017 · Exemples : Les sommes télescopiques sont une méthode très efficace pour calcu- ler la somme des termes d'une suite (un) Il s'agit de trouver
[PDF] Calculs de sommes et de produits finis
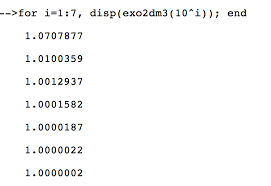
21 sept 2022 · Application[2504] 9 Somme téléscopique À l'aide d'un téléscopage de termes exprimer en fonction de n ? 2 la somme n ? k=2 ln
[PDF] Feuille dexercices no 5 - Sommes et produits
Reprendre la méthode de l'exercice précédent pour retrouver la formule de n ? k=0 k3 Exercice 10 Des sommes télescopiques Calculer les sommes suivantes
[PDF] Calcul de sommes et de produits
1 1 2 2 Sommes des entiers et somme des carrés ln ( sin (k? 2n )) ; poser k = 2n ? k 1 2 3 Sommes télescopiques Proposition 7
[PDF] Séries numériques - Xiffr
Calculer la somme lorsqu'il y a convergence (a) Étudier la suite de terme général ln(un+1) ? ln(un) k(k?1) et sommation télescopique) Au final
[PDF] Exercice Convergence de ? ln(1 ? 1 k2 ) et valeur de la somme de
Donc ?(an+1 ?an) converge absolument par règle de comparaison La série est téléscopique donc (an) converge et il existe ? tq an = ? + o(1)
Comment calculer la somme d'une série numérique ?
Lorsqu'une expression comporte plusieurs opérations, on peut se demander s'il s'agit d'une somme ou d'un produit. C'est une somme car : on commence le calcul par la multiplication, elle est prioritaire : 3 × 4 = 12 ; on effectue l'addition : 2 + 12 = 14.Comment calculer la somme d'un produit ?
Lorsque n augmente, sa n-ième somme partielle Sn augmente (lentement) et finit par dépasser tout nombre donné par avance : cette somme tend vers l'infini. La série harmonique ne converge pas, on dit qu'elle est divergente.Comment montrer qu'une série est divergente ?
Lorsqu'une telle série est convergente, on note ? n = n 0 + ? u n ou sa somme ? n = n 0 + ? u n (le choix de l'une ou l'autre notation étant d'ordre typographique et non mathématique) c'est-à-dire la limite de la suite ( ? k = n 0 n u k ) quand tend vers .
SériesDans ce chapitre nous allons nous intéresser à des sommes ayant une infinité de termes. Par exemple que peut bien
valoir la somme infinie suivante : 1+12 +14 +18 +116+=?2 11 21
4
Cette question a été popularisée sous le nom duparadoxe de Zénon. On tire une flèche à2mètres d"une cible. Elle
met un certain laps de temps pour parcourir la moitié de la distance, à savoir un mètre. Puis il lui faut encore du
temps pour parcourir la moitié de la distance restante, et de nouveau un certain temps pour la moitié de la distance
encore restante. On ajoute ainsi une infinité de durées non nulles, et Zénon en conclut que la flèche n"atteint jamais
sa cible! Zénon ne concevait pas qu"une infinité de distances finies puisse être parcourue en un temps fini. Et pourtant
nous allons voir dans ce chapitre que la somme d"une infinité de termes peut être une valeur finie.
1. Définitions - Série géométrique
1.1. DéfinitionsDéfinition 1.
Soit(uk)k>0une suite de nombres réels (ou de nombres complexes). On pose S n=u0+u1+u2++un=n X k=0u k. La suite(Sn)n>0s"appelle lasériede terme généraluk.Cette série est notée par la somme infinieX
k>0u k. La suite(Sn)s"appelle aussi lasuite des sommes partielles.Exemple 1.Fixonsq2C. Définissons la suite(uk)k>0paruk=qk; c"est une suite géométrique. Lasérie géométriqueX
k>0q kest la suite des sommes partielles : S0=1S1=1+q S2=1+q+q2...Sn=1+q+q2++qn...Définition 2.
SÉRIES1. DÉFINITIONS- SÉRIE GÉOMÉTRIQUE2Si la suite(Sn)n>0admet une limite finie dansR(ou dansC), on note
S=+1X k=0u k=limn!+1Sn.On appelle alorsS=P+1 k=0uklasommede la sérieP k>0uk, et on dit que la série estconvergente. Sinon, on ditqu"elle estdivergente.Notations.On peut noter une série de différentes façons, et bien sûr avec différents symboles pour l"indice :
+1X i=0u iX n2Nu nP k>0ukX u k. Pour notre part, on fera la distinction entre une série quelconque X k>0u k , et on réservera la notation +1X k=0u kà une série
convergente ou à sa somme.1.2. Série géométriqueProposition 1.
Soit q2C. La série géométriqueP
k>0qkest convergente si et seulement sijqj<1. On a alors+1X k=0q S n=1+q+q2+q3++qn. Écartons tout de suite le casq=1, pour lequelSn=n+1. Dans ce casSn!+1, et la série diverge.Soitq6=1 et multiplionsSnpar 1q:
(1q)Sn= (1+q+q2+q3++qn)(q+q2+q3++qn+1) =1qn+1 DoncS n=1qn+11qSijqj<1, alorsqn!0, doncqn+1!0 et ainsiSn!11q. Dans ce cas la sérieP k>0qkconverge.Sijqj>1, alors la suite(qn)n"a pas de limite finie (elle peut tendre vers+1, par exemple siq=2; ou bien être
divergente, par exemple siq=1). Donc sijqj>1,(Sn)n"a pas de limite finie, donc la sérieP k>0qkdiverge.Exemple 2.1.Série géométrique de raisonq=12:
+1X k=012 k =1112=2. Cela résout le paradoxe de Zénon : la flèche arrive bien jusqu"au mur! 2. Série géométrique de raisonq=13, avec premier terme133. On se ramène à la série géométrique commençant à
k=0en ajoutant et retranchant les premiers termes : +1X k=313 k +1X k=013 k 11313
2=1113
139=32
139=118.
3.Le fait de calculer la somme d"une série à partir dek=0est purement conventionnel. On peut toujours effectuer
un changement d"indice pour se ramener à une somme à partir de0. Une autre façon pour calculer la même série
+1X k=313 kque précédemment est de faire le changement d"indicen=k3 (et donck=n+3) : +1X k=313 k=+1X n=013 n+3=+1X n=013 313n=13 3+1X n=013 n=127 1113
=118 4. +1X 2k =+1X 14 k =1114 =45 SÉRIES1. DÉFINITIONS- SÉRIE GÉOMÉTRIQUE3
1.3. Séries convergentesLa convergence d"une série ne dépend pas de ses premiers termes : changer un nombre fini de termes d"une série
ne change pas sa nature, convergente ou divergente. Par contre, si elle est convergente, sa somme est évidemment
modifiée.Une façon pratique d"étudier la convergence d"une série est d"étudier son reste : lereste d"ordrend"une série
convergenteP+1 k=0ukest : R n=un+1+un+2+=+1X k=n+1u kProposition 2. Si une série est convergente, alors S=Sn+Rn(pour tout n>0) etlimn!+1Rn=0.Démonstration. •S=P+1 k=0uk=Pn k=0uk+P+1 k=n+1uk=Sn+Rn. DoncRn=SSn!SS=0 lorsquen!+1.1.4. Suites et sériesIl n"y a pas de différence entre l"étude des suites et des séries. On passe de l"une à l"autre très facilement.
Tout d"abord rappelons qu"à une sérieP
k>0uk, on associe la somme partielleSn=Pn k=0uket que par définition la série est convergente si la suite(Sn)n>0converge.Réciproquement si on veut étudier une suite(ak)k>0on peut utiliser le résultat suivant :Proposition 3.
Unesomme télescopiqueest une série de la formeX k>0(ak+1ak). Cette série est convergente si et seulement si`:=limk!+1akexiste et dans ce cas on a : +1X k=0(ak+1ak) =`a0.Démonstration. S n=n X k=0(ak+1ak) = (a1a0)+(a2a1)+(a3a2)++(an+1an) =a0+a1a1+a2a2++anan+an+1 =an+1a0Voici un exemple très important pour la suite.Exemple 3.
La série
+1X k=01(k+1)(k+2)=112+123+134+est convergente et a la valeur1. En effet, elle peut être écrite comme somme télescopique, et plus précisément la
somme partielle vérifie : S n=n X k=01(k+1)(k+2)=n X1k+11k+2
=11n+2!1 lorsquen!+1 Par changement d"indice, on a aussi que les sériesP+1 k=11k(k+1)etP+1 k=21k(k1)sont convergentes et de même somme1. SÉRIES1. DÉFINITIONS- SÉRIE GÉOMÉTRIQUE41.5. Le terme d"une série convergente tend vers0Théorème 1.
Si la sérieP
k>0ukconverge, alors la suite des termes généraux(uk)k>0tend vers0.Le point clé est que l"on retrouve le terme général à partir des sommes partielles par la formule
u n=SnSn1.Démonstration.Pour toutn>0, posonsSn=Pn
k=0uk. Pour toutn>1,un=SnSn1. SiP k>0ukconverge, la suite(Sn)n>0converge vers la sommeSde la série. Il en est de même de la suite(Sn1)n>1. Par linéarité de la limite, la
suite(un)tend versSS=0.La contraposée de ce résultat est souvent utilisée : Une série dont le terme général ne tend pas vers 0 ne peut pas converger.Par exemple les séries
P k>1(1+1k )etP k>1k2sont divergentes. Plus intéressant, la sériePukde terme général u k=1 sik=2`pour un certain`>00 sinon
diverge. En effet, même si les termes valant 1 sont très rares, il y en a quand même une infinité!
1.6. LinéaritéProposition 4.
SoientP+1
k=0aketP+1 k=0bkdeux séries convergentes de sommes respectivesAetB, et soient,2R(ouC). Alors la sérieP+1 k=0(ak+bk)est convergente et de sommeA+B. On a donc +1X k=0(ak+bk) =+1X k=0a k++1X k=0b k.Démonstration.A n =Pn k=0ak!A2C,Bn=Pn k=0bk!B2C. DoncPn k=0(ak+bk) =Pn k=0ak+Pn k=0bk=An+Bn!A+B.Par exemple :
+1X 12 k+53 k =+1X k=012 k+5+1X k=013 k=1112 +51113=2+532 =192
Comme application pour les séries à termes complexes, la convergence équivaut à celle des parties réelle et imaginaire :Proposition 5.
Soit(uk)k>0une suite de nombres complexes. Pour toutk, notonsuk=ak+ibk, avecakla partie réelle deuketbkla
partie imaginaire. La sériePukconverge si et seulement si les deux sériesPaketPbkconvergent. Si c"est le cas, on
a : +1X k=0u k=+1X k=0a k+i+1X k=0b k.Exemple 4. Considérons par exemple la série géométriqueP k>0rk, oùr=eiest un complexe de module <1et d"argument Comme le module derest strictement inférieur à 1, alors la série converge et +1X k=0r k=11r. SÉRIES1. DÉFINITIONS- SÉRIE GÉOMÉTRIQUE5 D"autre part,rk=keikpar la formule de Moivre. Les parties réelle et imaginaire derksont a k=kcos(k)etbk=ksin(k). On déduit de la proposition précédente que : +1X k=0a k=Re +1X k=0r k et+1X k=0b k=Im +1X k=0r kLe calcul donne :
+1X k=0 kcos(k) =1cos1+22coset+1X k=0 ksin(k) =sin1+22cos.1.7. Sommes de sériesPour l"instant, il n"y a pas beaucoup de séries dont vous connaissez la somme, à part les séries géométriques. Il faudra
attendre d"autres chapitres et d"autres techniques pour calculer des sommes de séries. Dans ce chapitre on s"intéressera
essentiellement à savoir si une série converge ou diverge.Voici cependant une exception!
Exemple 5.
Soitq2Ctel quejqj<1. Que vaut la somme
+1X k=0kq k? Admettons un moment que cette série converge et notonsS=P+1 k=0kqk.Écrivons :
S=+1X k=0kq k=+1X k=1kq k=q+1X k=1kq k1 =q+1X k=1q k1+q+1X k=1(k1)qk1 =q+1X k=1q k1+q+1X k 0=0k0qk0en posantk0=k1
=q+1X k=1q k1+qS En résolvant cette équation enS, on trouve que (1q)S=q+1X k=1q k1.Cette dernière série est une série géométrique de raisonqavecjqj<1donc converge. Cela justifie la convergence de
S. Ainsi (1q)S=q11q.Conclusion :
S=+1X k=0kq k=q(1q)2.1.8. Critère de Cauchy
Attention!
Il existe des sériesP
k>0uktelles quelimk!+1uk=0, maisP k>0ukdiverge. L"exemple le plus classique est lasérie harmonique:La série X k>11k =1+12 +13 +14 +diverge SÉRIES1. DÉFINITIONS- SÉRIE GÉOMÉTRIQUE6Plus précisément, on a lim
n!+1Sn= +1. Cependant on auk=1k !0 (lorsquek!+1). Pour montrer que la série diverge nous allons utiliser le critère de Cauchy.Rappel.Une suite(sn)de nombres réels (ou complexes) converge si et seulement si elle est une suite de Cauchy,
c"est-à-dire :8 >09n02N8m,n>n0jsnsmj<
Pour les séries cela nous donne :Théorème 2(Critère de Cauchy).Une série
+1X k=0u kconverge si et seulement si8 >09n02N8m,n>n0un++um< .On le formule aussi de la façon suivante :
8 >09n02N8m,n>n0
m X k=nu k ou encore8 >09n02N8n>n08p2Nun++un+p<
Démonstration.
La preuve est simplement de dire que la suite(Sn)des sommes partielles converge si et seulement si c"est une suite de Cauchy. Ensuite il suffit de remarquer queSmSn1=un++um.Revenons à la série harmoniqueP
k>11k. La somme partielle estSn=Pn k=11k. Calculons la différence de deux sommespartielles, afin de conserver les termes entren+1 (qui joue le rôle den) et 2n(qui joue le rôle dem) :
Squotesdbs_dbs8.pdfusesText_14[PDF] somme télescopique exercice corrigé
[PDF] série téléscopique exercice
[PDF] somme télescopique suite
[PDF] somme telescopique convergence
[PDF] somme théologique iii
[PDF] saint thomas d aquin wikipedia
[PDF] somme théologique saint thomas pdf
[PDF] le chat et les pigeons pdf
[PDF] obligation d être prof principal
[PDF] décret no 93-55 du 15 janvier 1993
[PDF] bo n°5 du 4 février 1993
[PDF] je ne vois dans tout animal qu'une machine ingénieuse these
[PDF] explication de texte philosophie rousseau discours sur l origine
[PDF] différents aspects du travail
