[PDF] [PDF] Calculs de sommes et de produits finis





Previous PDF Next PDF



Feuille dexercices n˚8 : corrigé

13 déc. 2011 1. 2 . • On reconnait une somme télescopique dans la somme partielle : n. ∑ k=1 ln. (k + 1 k. ) = n. ∑ k=1 ln(k +. 1) − lnk = ln(n + 1) − ln ...



Exercice. Convergence de ∑ ln(1 − 1 k2 ) et valeur de la somme de

Donc ∑(an+1 −an) converge absolument par règle de comparaison. La série est téléscopique donc (an) converge et il existe γ tq an = γ + o(1).



Séries

(somme télescopique). Si la série de terme général un converge alors limn→+∞ un = 0 et donc 0 < un. ∼ n→+∞ ln(1+un). Donc la série de terme général ln(1 



[PDF] Séries - Exo7 - Cours de mathématiques

En effet elle peut être écrite comme somme télescopique



Somme téléscopique À laide dun téléscopage

25 sept. 2021 — On mobilisera les propriétés opératoires de la fonction logarithme pour cela. Éléments de correction. On a tout d'abord que : ∀k ∈ 2; n ln.



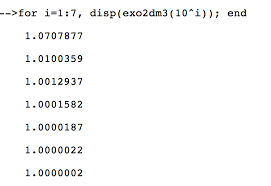Devoir Maison n 3 Devoir Maison n 3

On va majorer chaque terme de la somme par ln(k)−ln(k −1). Cependant l On reconnaîtra ensuite une somme télescopique. vn. = 1+ n. ∑ k=2. 1 k. ≤ 1 + n.



Sommes et Produits 1 Sommes

S3 = ln 2 + ln 4 + ln 6 + + ln 12. S4 = 1 − 2+3 − 4 + ... − 102 + 103 ... On parle de somme télescopique lorsque le terme général est la différence ...



Calculs de sommes et de produits finis

10 août 2023 Sommes téléscopiques. Proposition 4



Les symboles somme et produit - Lycée dAdultes

27 fév. 2017 k. • On utilise une somme télescopique : Sn − xSn = n. C k=p x k ... ln ak. 2.3 Produits télescopiques. Théorème 7 : Produits télescopiques.



Feuille dexercices no 5 - Sommes et produits

Des sommes télescopiques. Calculer les sommes suivantes : 1. (#) A = n. ∑ k=1 ln(k + 1) − ln k = ln(n + 1) − ln(1) = ln(n + 1). 19. n. ∑ k=0. 1. (k + 2)(k ...



Feuille dexercices n?8 : corrigé

13 déc. 2011 On reconnait une somme télescopique dans la somme partielle : ... ln 2. Exercice 2 (**). Le plus simple pour déterminer la nature de la ...



Exercice. Convergence de ? ln(1 ? 1 k2 ) et valeur de la somme de

Donc ?(an+1 ?an) converge absolument par règle de comparaison. La série est téléscopique donc (an) converge et il existe ? tq an = ? + o(1).



Séries

(somme télescopique). Si la série de terme général un converge alors limn?+? un = 0 et donc 0 < un. ? n?+? ln(1+un). Donc la série.



Les symboles somme et produit - Lycée dAdultes

27 févr. 2017 entiers naturels n et p tels que p ? n on définit la somme suivante par ... ln ( n n k=p ak) = n. C k=p ln ak. 2.3 Produits télescopiques.



Séries

En effet elle peut être écrite comme somme télescopique



Calculs de sommes et de produits finis

13 sept. 2021 Application



Séries

16 mars 2020 ln(n). = 1. Par théorème d'encadrement on trouve ainsi que lim n?+?. Sn ln(n) ... n+1



Sommes et produits de nombres

ln( k2. (k ? 1)(k + 1)) . Exercice 6 : Écrire à l'aide de factorielles les expressions suivantes : (a) n.



Feuille dexercices n?21 : corrigé

5 juin 2014 u0 ? un+1 = u0 donc la série de terme général u2 n converge vers u0. 3. La somme partielle va également être télescopique : k=n. ? k=0 ln.



Compléments sur les suites Suites adjacentes - Correction - Lycée d

27 févr. 2017 Comme la dernière somme est télescopique on a un ? ln(n + 1) ? ln 1 ? un ? ln(n + 1) or lim n?+? ln(n + 1)=+?



[PDF] [PDF] Séries - Exo7 - Cours de mathématiques

Une somme télescopique est une série de la forme ? k?0 (ak+1 ? ak) Cette série est convergente si et seulement si l := limk?+? ak existe et dans ce 



[PDF] Feuille dexercices n?8 : corrigé - Normale Sup

13 déc 2011 · On reconnait une somme télescopique dans la somme partielle : n ? k=1 ln (k + 1 k ) = n ? k=1 ln(k + 1) ? lnk = ln(n + 1) ? ln 1



[PDF] Devoir Maison n?3

On reconnaîtra ensuite une somme télescopique vn = 1+ n ? k=2 1 k ? 1 + n ? k=2 (ln(k) ? ln(k ? 1)) ? 1 + ln(n) ? ln(2 ? 1) ? 1 + ln(n)



[PDF] Les symboles somme et produit - Lycée dAdultes

27 fév 2017 · Exemples : Les sommes télescopiques sont une méthode très efficace pour calcu- ler la somme des termes d'une suite (un) Il s'agit de trouver 



[PDF] Calculs de sommes et de produits finis

21 sept 2022 · Application[2504] 9 Somme téléscopique À l'aide d'un téléscopage de termes exprimer en fonction de n ? 2 la somme n ? k=2 ln



[PDF] Feuille dexercices no 5 - Sommes et produits

Reprendre la méthode de l'exercice précédent pour retrouver la formule de n ? k=0 k3 Exercice 10 Des sommes télescopiques Calculer les sommes suivantes 



[PDF] Calcul de sommes et de produits

1 1 2 2 Sommes des entiers et somme des carrés ln ( sin (k? 2n )) ; poser k = 2n ? k 1 2 3 Sommes télescopiques Proposition 7



[PDF] Séries numériques - Xiffr

Calculer la somme lorsqu'il y a convergence (a) Étudier la suite de terme général ln(un+1) ? ln(un) k(k?1) et sommation télescopique) Au final



[PDF] Exercice Convergence de ? ln(1 ? 1 k2 ) et valeur de la somme de

Donc ?(an+1 ?an) converge absolument par règle de comparaison La série est téléscopique donc (an) converge et il existe ? tq an = ? + o(1)

  • Comment calculer la somme d'une série numérique ?

    Lorsqu'une expression comporte plusieurs opérations, on peut se demander s'il s'agit d'une somme ou d'un produit. C'est une somme car : on commence le calcul par la multiplication, elle est prioritaire : 3 × 4 = 12 ; on effectue l'addition : 2 + 12 = 14.

  • Comment calculer la somme d'un produit ?

    Lorsque n augmente, sa n-ième somme partielle Sn augmente (lentement) et finit par dépasser tout nombre donné par avance : cette somme tend vers l'infini. La série harmonique ne converge pas, on dit qu'elle est divergente.

  • Comment montrer qu'une série est divergente ?

    Lorsqu'une telle série est convergente, on note ? n = n 0 + ? u n ou sa somme ? n = n 0 + ? u n (le choix de l'une ou l'autre notation étant d'ordre typographique et non mathématique) c'est-à-dire la limite de la suite ( ? k = n 0 n u k ) quand tend vers .

BL | 1

e& 2eannéeChapitre | CL01

Calculs de sommes et de produits finis

Version du 10-08-2023 à 12:11

Contexte

Dans tout ce chapitre,n,petqdésigneront des entiers naturels et(uk)k∈Ndésigne une suite de nombres réels.1.Le symbole de sommationΣDéfinition 1| Le symboleΣSens du symbole

Lasommeu0+u1+...+undesn+ 1premiers termes de la suite(uk)k∈Nest notéen X k=0u k. On lit cette écriture " somme dek= 0jusqu"àndeuk».Nombre de termes de la somme n X k=0u k=u

0+u1+u2+...+un|{z}

il y an+ 1termesLa " variable »kest appeléeindicede la somme ou que lasomme est indexée park.Extension de la notation

Lasommeup+up+1+...+uqdes termes de la suite(uk)k∈Ndont les indices sont compris entrepetqavec k=pu k=u p+up+1+...+uq|{z} il y aq-p+ 1termesIllustration 6 X k=0=u

0+u1+u2+u3+u4+u5+u6u

0+u1+u2+u3+u4=4

X k=0u k9 X k=3=u

3+u4+u5+u6+u7+u8+u9u

5+u6+u7+u8+u9+u10=10

X k=5u kApplication 1|Réf.2490Écrire les sommes à l"aide du symbole X:

1.S1= 1 +12

+13 +14 +15 +...+115

2.S2= 32+ 42+...+ 872;

3.S3=23

+34
+45
+...+1415

4.S4= 2×3 +×3×4 +...+ 15×16;

5.S5= 1 + 2 + 4 + 8 +...+ 1024;CPGE-BL | 1

e& 2eannée|Mathématiques Version du 10-08-2023 à 12:111CL01| Calculs de sommes et de produits finis

BL | 1

e& 2eannéeApplication 2|Réf.2491Écrire explicitement les sommes : A=5X k=012k+ 1etB=7X k=32k2k-1 puis les calculer.Théorème 1| Sommes des premiers entiers et des puissances Sommes desnpremiers entiers∀n∈N∗,nX k=1k=n(n+ 1)2

Illustration

1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 =8×(8 + 1)2

=8×92 =72 2=36

Cette formule est encore vraie si l"indice

de départ est0:nX k=0k=n(n+ 1)2Somme desn+ 1premières puissances∀q̸= 1,∀n∈N,nX k=0q k=1-qn+11-qIllustration 2

0+ 21+ 22+ 23+ 24=1-24+11-2=1-251-2=1-32-1=31

Éléments de preuve:

Application 3|Réf.2494Calculer les sommes suivantes en donnant le résultat sous forme fractionnaire :

1.S1=192X

k=1k;

2.S2=8X

k=0(-3)k;3.S3=10X k=012 k

4.S4=9X

k=0 -110 kCPGE-BL | 1 e& 2eannée|Mathématiques Version du 10-08-2023 à 12:112CL01| Calculs de sommes et de produits finis

BL | 1

e& 2eannée2.Manipuler les sommes finiesProposition 1| Relation de Chasles Pour tout entier natureln0∈Jp;qKavecp < q, on a :qX k=pu k= n 0X k=pu qX k=n0+1u k!Application au calcul des sommes tronquées

Pour tousp < q:qX

k=pu k=q X k=0u k-p-1X k=0u kIllustration 38
X k=12k=24X k=12k+ 38X
k=25k38 X k=12k=38X k=1k- 11X

k=1kApplication 4|Réf.2496Calculer les sommes suivantes en donnant le résultat sous forme fractionnaire :

1.S1=192X

k=125k;

2.S2=8X

k=4(-3)k;3.S3=10X k=312 k

4.S4=9X

k=2 -110 kProposition 2| Opérations sur les sommes de même indexation Pour(uk)k∈Net(vk)k∈Ndeux suites de réels :Pour tout réelλ:qX k=p(λuk) =λ× qX k=pu q X k=p(uk+vk) = qX k=pu qX k=pv Linéarité de la somme q X k=p(λuk+vk) =λ qX k=pu qX k=pv Illustration 12 X k=3(2k) =2 12X k=3k!21 X k=9 k+k2= 21X
k=9k! 21X
k=9k 2!21 X k=9

3k+ 4k2=3

21X
k=9k! + 4 21X
k=9k

2!CPGE-BL | 1

e& 2eannée|Mathématiques Version du 10-08-2023 à 12:113CL01| Calculs de sommes et de produits finis

BL | 1

e& 2eannéeApplication 5|Réf.2499Exprimer en fonction denles sommes : S 1=nX k=0(2k)etS2=nX k=1(2k-1)3.Changement d"indice dans une sommeIntroduction | Histoire de décalage

On a :

10X k=0ln(k+ 3) =Mais on a aussi : 13X i=3ln(i) =Ainsi : La relation entre les deux indices de ces sommes est.

Proposition 3| Changement d"indice dans une somme

Lechangement d"indicek=ℓ-plaisse la sommenX

k=0u kinchangée :n X k=0u k=n+pX ℓ=pu ℓ-pIllustration 10 X i=0u i=10+3 X ℓ=0+3u ℓ-3=13 X ℓ=3u ℓ-313 X k=4u k=13-4X i=4-4u i+4=9 X i=0u i+412 X m=3u m+2=12+2 X n=3+2u n=14 X n=5u nMéthode 1| [ halign=center]Effectuer un changement d"indice dans une somme

Ancien indice :k

Nouvel indice :ℓRelation entrek

etℓde la forme k=ℓ±poùp∈NCalcul des nou- velles bornes : quandk=... on aℓ=...Transformation du terme général de la somme : " on remplace kparℓ±p»Application 6|Réf.2500Effectuer un changement d"indice dans la somme n+1X

k=3ln(k)de sorte que la somme soit indexée à partir de0.Application 7|Réf.2501Effectuer un changement d"indice dans la somme

nX k=0(k+ 2)2de sorte que le terme général de la somme deviennei2oùi est le nouvel indice de sommation.CPGE-BL | 1 e& 2eannée|Mathématiques Version du 10-08-2023 à 12:114CL01| Calculs de sommes et de produits finis

BL | 1

e& 2eannée4.Sommes téléscopiquesProposition 4| Téléscopage de termes

Le premier moins le dernier

k=p(uk-uk+1) =up-un+1Illustration | Justification 12 X k=3(uk-uk+1) = (u3-u4) + (u4-u5) +...+ (u12-u13) =u3-u13Le dernier moins le premier n X k=p(uk+1-uk) =un+1-upIllustration | Justification 12 X k=3(uk+1-uk) = (u4-u3) + (u5-u4) +...+ (u13-u12) =u13-u3On parle dans ce cas desommes téléscopiquesaIllustration 18 X k=3(ln(k)-ln(k+ 1)) = ln(3)-ln(18)18 X

k=3(ln(k+ 1)-ln(k)) = ln(18-ln(3)a. notamment lorsque le terme général de la somme s"exprime comme la différence de deux termes successifs d"une même suite.Éléments de preuve:

C"est une conséquence de la linéarité de la somme et d"un changement d"indice.Méthode 2| Calculer une somme à l"aide d"un téléscopage

•on essaie de transformer le terme général de la somme de sorte à écrire la somme sous la forme...X

k=...(uk+1-uk) ou ...X k=...(uk-uk+1);

•on détermine les deux termes qui restent à l"issue du télescopage.Application 8|Réf.2503Calculer

nX k=11k(k+ 1)oùn≥1, en remarquant que :∀k∈N∗,1k(k+ 1)=1k

-1k+ 1Application 9|Réf.2504À l"aide d"un téléscopage de termes, exprimer en fonction den≥2la sommenX

k=2ln 1-1k .CPGE-BL | 1 e& 2eannée|Mathématiques Version du 10-08-2023 à 12:115CL01| Calculs de sommes et de produits finis

BL | 1

e& 2eannée5.Produits finisDéfinition 2| Le symbole

YSens du symbole

Leproduitu0×u1×...×undesn+ 1premiers termes de la suite(uk)k∈Nest notéen Y k=0u k. On lit cette écriture" produit dek= 0jusqu"àndeuk».Nombre de facteurs du produit n Y k=0u k=u

0×u1×u2×...×un|{z}

il y an+ 1facteursLa " variable »kest appeléeindicedu produit ou que leproduit est indexé park.Extension de la notation

Leproduitup×up+1×...×uqdes termes de la suite(uk)k∈Ndont les indices sont compris entrepetqavec

k=pu k=u p×up+1×...×uq|{z} il y aq-p+ 1facteursIllustration 6 Y k=0=u

0×u1×u2×u3×u4×u5×u6u

0×u1×u2×u3×u4=4

Y k=0u k9 Y k=3=u

3×u4×u5×u6×u7×u8×u9u

5×u6×u7×u8×u9×u10=10

Y k=5u kApplication 10|Réf.2507Écrire à l"aide du symbole

Y, le produit12

×14

×16

×...×120

.CPGE-BL | 1 e& 2eannée|Mathématiques Version du 10-08-2023 à 12:116CL01| Calculs de sommes et de produits finis

BL | 1

e& 2eannéeProposition 5| Relation de Chasles

Pour tout entier natureln0∈Jp;qKavecp < qq

Y k=pu k= n 0Y k=pu qY k=n0+1u k!Produits tronqués | Pour toutp < qq Y k=pu k=q Y k=0u kp-1Y k=0u kSous réserve que la suite ne s"annule pas....Illustration 22
Y k=8u k= 13Y k=8u k! 22Y
k=14u k!16 Y k=8u k=16 Y k=0u k7 Y k=0u kProposition 6| Opérations sur les produits de même indexation Pour(uk)k∈Net(vk)k∈Ndeux suites de réels etλ∈R:q Y k=p(uk×vk) = qY k=pu qY k=pv 24 Y k=8 k2(k+ 1)= 24Y
k=8k 2! 24Y
k=8(k+ 1)!q Y k=p(λuk) =λ q-p+1× qY k=pu 21 Y k=7(2k) =2

21-7+1×

21Y
k=7k!Proposition 7| Changement d"indice dans un produit Lechangement d"indicek=ℓ-plaisse le produitnY k=0u kinchangé :nY k=0u k=n+pY ℓ=pu ℓ-pProposition 8| Téléscopage de facteurs

Le premier sur le dernier

k=p uku k+1 =u pu n+1Le dernier sur le premier k=p uk+1u k =u n+1u pIllustration | Justification 31
Y k=12u ku k+1=u 12u

13×u13u

14×...×u30u

31×u31u

32=u
12u

32On parle dans ce cas deproduits téléscopiques.CPGE-BL | 1

e& 2eannée|Mathématiques Version du 10-08-2023 à 12:117CL01| Calculs de sommes et de produits finis

BL | 1

e& 2eannéeApplication 11|Réf.2510Donner une autre écriture du produitP=14Y k=42 k-2à l"aide du symboleY.Proposition 9| Passer d"un produit à une somme et vice-versa Les opérations sur la fonction exponentielle donnent :

Somme vers produit

exp nX k=0u k! =nY k=0e ukProduit vers somme ln nY k=0u k! =nX k=0ln(uk)Sous réserve que :∀k∈N, uk>0CPGE-BL | 1 e& 2eannée|Mathématiques Version du 10-08-2023 à 12:118CL01| Calculs de sommes et de produits finis

BL | 1

e& 2eannée6.Factorielle d"un entier et coefficients binomiauxDéfinition 3| Factorielle d"un entier naturel

On appellefactorielle denle nombre entier que l"on noten!, que l"on lit " factoriellen» défini par :Définition formelle

n! = 1sin= 0 nY

k=1ksin≥1On a donc :0! = 1Explicitation den!n! =1×2×3×...×(n-1)×nRelation fondamentale

Pourn≥1:n! = (n-1)!×nIllustration | Calcul de quelques valeurs 7! =7 Y k=1k=1×2×3|{z} =6×4×5×6|{z} =120×7=6×120|{z} =720×7=50408! =(8-1)!×8=7!×8=5040×8=4032010! = 3628800

15! = 1307674368000

quotesdbs_dbs45.pdfusesText_45
[PDF] somme changement d'indice

[PDF] somme télescopique exercice corrigé

[PDF] série téléscopique exercice

[PDF] somme télescopique suite

[PDF] somme telescopique convergence

[PDF] somme théologique iii

[PDF] saint thomas d aquin wikipedia

[PDF] somme théologique saint thomas pdf

[PDF] le chat et les pigeons pdf

[PDF] obligation d être prof principal

[PDF] décret no 93-55 du 15 janvier 1993

[PDF] bo n°5 du 4 février 1993

[PDF] je ne vois dans tout animal qu'une machine ingénieuse these

[PDF] explication de texte philosophie rousseau discours sur l origine

[PDF] différents aspects du travail