 RÉSOLUTION DE SYSTÈMES À DEUX INCONNUES
RÉSOLUTION DE SYSTÈMES À DEUX INCONNUES
Méthode des combinaisons linéaires . Solution d'un système d'équations ... 1 2 est une solution du système d'équations linéaires. 2 3 8.
 SYSTÈMES DÉQUATIONS ET DROITES
SYSTÈMES DÉQUATIONS ET DROITES
Dans ce chapitre on verra deux méthodes permettant de résoudre de tels systèmes. Partie 1 : Méthode de substitution. Méthode : Résoudre un système d'équations
 Titre : METHODES DADDITION ET DE CRAMER
Titre : METHODES DADDITION ET DE CRAMER
Cette méthode est aussi appelée méthode des combinaisons ou méthode de réduction au même coefficient. Résoudre le système suivant : 3 x + 2 y = 10 (1). 4 x - y
 SYSTEMES DEQUATIONS
SYSTEMES DEQUATIONS
Méthode : Résoudre un système d'équations pas la méthode des combinaisons d'éliminer une inconnue par soustraction ou addition des deux équations.
 EQUATIONS DE DROITES SYSTEMES DEQUATIONS
EQUATIONS DE DROITES SYSTEMES DEQUATIONS
Méthode de résolution par substitution : on vérifie que le système a une seule solution en écrivant les deux équations réduites. on a alors isolé l' inconnue y.
 CHAPITRE 1 Systèmes déquations et dinéquations linéaires I
CHAPITRE 1 Systèmes déquations et dinéquations linéaires I
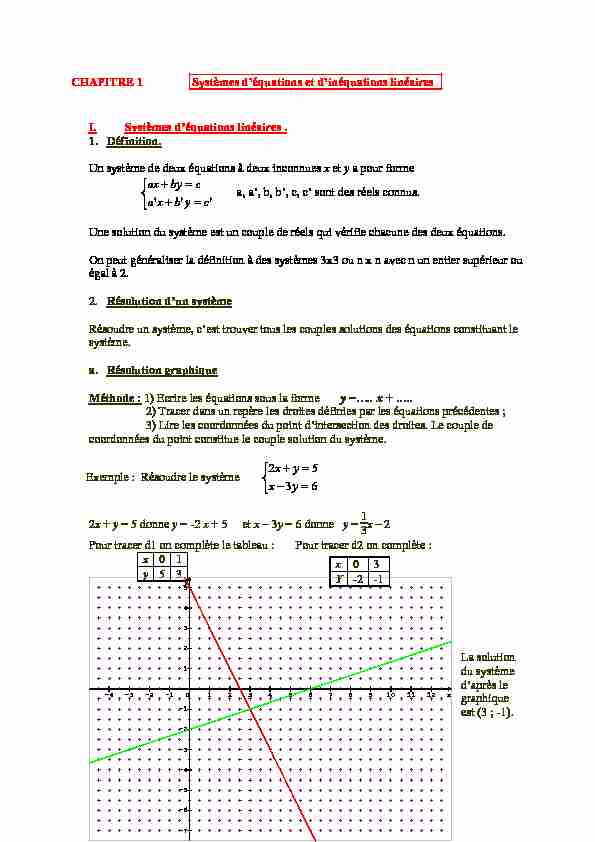
La solution du système d'après le graphique est (3 ; -1). x 0 3. Y -2 -1. Page 2. b. Résolution par substitution.
 FICHE PÉDAGOGIQUE DE PRÉPARATION DUNE LEÇON Classe
FICHE PÉDAGOGIQUE DE PRÉPARATION DUNE LEÇON Classe
Pour résoudre un système de deux équations du premier degré à deux inconnues par combinaison linéaire on procède comme dans l'activité suivante. 1.1 Activité.
 Untitled
Untitled
8 mars 2018 solution particuli`ere (12
 Ift 2421 Chapitre 3 Résolution des systèmes déquations linéaires
Ift 2421 Chapitre 3 Résolution des systèmes déquations linéaires
Résoudre L . y = b par substitution avant. 2. Résoudre U . x = y par substitution arrière.
 Systèmes déquations linéaires
Systèmes déquations linéaires
Systèmes d'équations linéaires. Corrections d'Arnaud Bodin. Exercice 1. 1. Résoudre de quatre manières différentes le système suivant (par substitution
 THÈSE - Archive ouverte HAL
THÈSE - Archive ouverte HAL
Un couple de nombres qui vérifie les deux équations est appelé solution du système Ici le coupe (1 ; 2) est solution En effet : 2×1?2=0 3×1?4×2=?5 Dans ce chapitre on verra deux méthodes permettant de résoudre de tels systèmes Partie 1 : Méthode de substitution
 Searches related to résoudre un système d+équation par combinaison PDF
Searches related to résoudre un système d+équation par combinaison PDF
Title: comment resoudre un systeme - methode par combinaison pdf Author: swiners Created Date: 6/28/2019 9:49:55 AM
Introduction
La seconde méthode élémentaire de résolution des systèmes d'équations linéaires est la méthode par combinaisons. Elle consiste à manipuler les différentes lignes du système, en les ajoutant, les multipliant, les soustrayant, pour éliminer des termeset résoudre le système.
Exemple
Résolution détaillée
Comment résoudre un système d’équation ?
Pour résoudre ce système d‘équation, il faut faire appel à l‘une des méthodes existantes. On optera ici pour la méthode de Galerkin connue par la simplicité de sa formulation et la généralisation de son application. III.6.2. Application de la méthode de Galerkin
Comment résoudre les deux équations?
Les deux équations forment un système d’équations du premier degré à deux inconnues.Sa résolution est assez simple, il suf?t de constater que les seconds membres des deux équations sont égaux.On peut développer de la façon sui- vante:
Comment résoudre un système d’équations à deux variables?
• Lorsqu’un problème comprend deux inconnues, un système d’équations à deux variables peut permettre de le résoudre. • our trouver la solution anément les équations. • On peut résoudre un système d’équations à l’aide d’une able de valeurs ou d’un graphique. he la solution du système d’équations : H 1 +5
Comment résoudre un système d'équations linéaires ?
La seconde méthode élémentaire de résolution des systèmes d'équations linéaires est la méthode par combinaisons. Elle consiste à manipuler les différentes lignes du système, en les ajoutant, les multipliant, les soustrayant, pour éliminer des termes et résoudre le système.
2 3 4 5 6 7 8 9 10 11 12-1-2-3-42
345-1 -2 -3 -4 -5 -6 -70 1 1 xy CHAPITRE 1 Systèmes d"équations et d"inéquations linéaires I.
Systèmes d"équations linéaires .
1. Définition.
Un système de deux équations à deux inconnues x et y a pour forme """cybxacbyax a, a", b, b", c, c" sont des réels connus. Une solution du système est un couple de réels qui vérifie chacune des deux équations.On peut généraliser la définition à des systèmes 3x3 ou n x n avec n un entier supérieur ou
égal à 2.
2. Résolution d"un système
Résoudre un système, c"est trouver tous les couples solutions des équations constituant le système. a. Résolution graphiqueMéthode :
1) Ecrire les équations sous la forme y =..... x + .....
2) Tracer dans un repère les droites définies par les équations précédentes ;
3) Lire les coordonnées du point d"intersection des droites. Le couple de
coordonnées du point constitue le couple solution du système.Exemple : Résoudre le système
6352yxyx
2x + y = 5 donne y = -2 x + 5 et x - 3y = 6 donne y = 1
3x - 2
Pour tracer d1 on complète le tableau : Pour tracer d2 on complète : x 0 1 y 5 3La solution
du système d"après le graphique est (3 ; -1). x 0 3Y -2 -1
b. Résolution par substitutionMéthode :
on exprime une des inconnues en fonction des autres puis on remplace l"inconnue par cette expression dans les autres équations. On se ramène ainsi à larésolution de système 2 x 2 ou encore à la résolution d"un équation à une inconnue.
Exemple : Résoudre le système
333222072411033
lzyxlzyxlzyx1) on utilise la ligne l1 pour exprimer y en fonction x et z.
y=3x+3z-102) on remplace y par 3x+3z-10 dans l2 et l3
3)1033(32207)1033(24
zzxxzzxx 3) on obtient le système (S")2710702
zxzxOn résoud ce système en posant z = 2x
D"où -7x-10(2x) = -27
-27 x = -27 x = 1.Et donc z = 2.
4) on remplace x par 1 et z par 2 dans l1 :163101033
yyzyx5) on vérifie que le triplet ( 1 ;-1 ;2) et bien solution des trois équations.
c.Résolution par combinaison linéaire
Cette méthode consiste à faire disparaître des inconnues en additionnant membres à membres des équations après avoir multiplié certaines d"entre elles par un réel convenablement choisie.Etude d"un exemple :
Résoudre le système (S)
)3(0)2(124)1(124 zyxzyxzyx 1 re étape : nous remarquons qu"en additionnant (1) et (2), nous obtenons une équation où ne figure plus que deux inconnues x et z :8x + 2z = 2 (4)
2ème étape : nous cherchons à obtenir une nouvelle équation où ne figure plus que x et z.
Pour cela, nous pouvons multiplier (3) par 2 et ajouter cette nouvelle équation à l"équation
(2). Nous obtenons alors6x + 3z =1 (5) .
On résoud le système :
136228
zxzxIl admet pour solution
3 1 31-==zetx
3ème étape : nous reportons les valeurs de x et y dans une des 3 équations du départ, par
exemple dans (3) y=0. 4 ème étape : il suffit de vérifier que le triplet ( 1 3 ; 0 ; -13) est bien solution du système (S).
Exercice : résoudre le système
112354739452
zyxzyxzyx d.Pivot de gauss.
La méthode de Gauss consiste à transformer un système en un système équivalent (c"est-
à-dire en un système admettant les mêmes solutions ) par utilisation des seuls opérations
élémentaires suivantes sur les lignes :
échange de deux lignes ;
multiplication d"une ligne par un nombre non nul addition d"une ligne avec une autre ligne pouvant avoir été multipliée.Le but est d"obtenir un système triangulaire.
Résolvons le système suivant (s)
?????x+10y-3z=52x-y+2z=2
-x+y+z=-3 1ère étape :
Eliminons x dans l"équation (2) e (3) en utilisant l"équation (1). multiplions l"équation (1) par -2 ; ajoutons membre à membre la nouvelle équation ainsi obtenue et l"équation (2) ; nous obtenons l"équation : -21 y + 8z = -8 (2"). ajoutons membre à membre les équations (1) et (3) ; nous obtenons l"équation :11y - 2z = 2 (3")
Ecrivons alors le système (S
1) suivant, dans lequel :
l"équation (1) du système initial (S) est conservée ; l"équation (2) est remplacée par (2") ; l"équation (3) est remplacée par (3") ; (S 1)221188215310
zyzyzyx 2ème étape :
Eliminons y dans l"équation (3") en utilisant l"équation (2"). Multiplions l"équation (2") par 11 21et ajoutons membre à membre la nouvelle équation ainsi obtenue et l"équation (3") ; nous obtenons l"équation : A
2 3 4 5 6 7 8-1-2-3-4-5-6-7-82
3456-1 -2 -3 -4 -5 -60 1 1 xy A
4621 z = -4621 (3"").
Nous pouvons donc écrire le système (S") suivant, dans lequel les équations (1) et (2") du système (S1) sont conservées et l"équation (3") est remplacée par (3"") :
(S") 2146
214688215310
z zyzyx 3ème étape : résolution
(S) a même ensemble de solutions que le système triangulaire (S") que l"on sait résoudre facilement. Le triplet solution du système est ( 2 ; 0 ; -1)II. Systèmes d"inéquations linéaires
1. Inéquation linéaire à deux inconnues ;
Soient a,b et c trois réels tels que (a ;b) ≠(0 ;0). Dans un repère, d est la droite d"équation ax + by + c =0. Dans ce repère, l"ensemble des points M (x ; y ) tels que ax + by +c > 0 est un demi-plan de frontière d, qui ne contient pas d. L"autre demi-plan, la frontière d étant exclue, est l"ensemble des points M (x ; y) tels que ax + by +c <0.Exemple : résolution graphique de
2x + 3y -6 < 0 ;
Dans un repère d"origine O, on
trace la droite d d"équation 2x + 3y -6 = 0 .L"ensemble des points M (x ; y) tels
que 2x + 3y -6 < 0 est un demi- plan de frontière d. Les coordonnées de O ( 0 ; 0) vérifient l"inéquation donc les solutions de l"inéquation sont représentées par le demi-plan contenant O.2. Système d"inéquations linéaires à deux inconnues.
Résoudre graphiquement un système d"inéquations linéaires à deux inconnues, c"estreprésenter dans un repère l"ensemble des points M dont les coordonnées (x ; y) vérifient
simultanément toutes les inéquations du système.2 3 4 5 6 7 8 9 10 11 12 13 14 15-12
34567-1 -2 -3 -40 1 1 xy
Exemple : Résolution graphique du système
27340923
xyyx.D est la droite d"équation 3x - 2y - 9 = 0.
D" est la droite d"équation 4y +3x = 27.
Les coordonnées de O (0 ; 0) vérifient la première inéquation car l"inégalité090203<-×-× est vraie.
Les coordonnées de O (0 ; 0) vérifient la deuxième inéquation car l"inégalité270304
<×+× est vraie. Donc les demi-plans qui représentent les solutions des deux inéquations du système sont respectivement les demi-plans de frontièresD et D", contenant le point O.
Les solutions du système sont représentées par le domaine non hachuré.quotesdbs_dbs33.pdfusesText_39[PDF] méthode de substitution microéconomie
[PDF] système par addition
[PDF] equation a 2 inconnues substitution
[PDF] telecharger methode rose piano gratuit pdf
[PDF] comment faire un diaporama sur open office
[PDF] telecharger powerpoint
[PDF] méthode de cramer pdf
[PDF] comment faire un bilan comptable pdf
[PDF] faire un bilan comptable exemple
[PDF] faire un bilan comptable exercice
[PDF] logiciel bilan comptable
[PDF] faire un bilan synonyme
[PDF] exemple bilan financier
[PDF] comment faire aimer la lecture ? mon fils de 9 ans
