[PDF] Soit f une fonction définie sur un intervalle I de R et a un réel

View - Download Soit f une fonction définie sur un intervalle I de R et a un réel

Previous PDF

Next PDF

Lycée JANSON DE SAILLY20 novembre 2014

DÉRIVATION1reSTI2D

I NOMBRE DÉRIVÉ

1 -DÉFINITION

Soitfune fonction définie sur un intervalleIdeRetaun réel appartenant àI.

Lorsque le rapport

f(x)-f(a) x-aadmet une limite réelle quandxtend versaen restant dansI, on dit que la

fonctionfest dérivable enaet cette limite réelle, notéef?(a), est appelée le nombre dérivé defena.

On note alors :

f ?(a) =limx→af(x)-f(a) x-a

2 -TANGENTE À UNE COURBE

Soitfune fonction définie sur un intervalleI, dérivable en aoùaest un réel deI, etCfsa courbe représentative dans un repère du plan. La droite passant par le pointA(a;f(a))de la courbeCf et de coefficient directeurf?(a)est appelée la tangente à la courbeCfau point d"abscissea.

0xy?i?

j af(a)A

PROPRIÉTÉ

Soitfune fonction définie sur un intervalleI, dérivable enaoùaest un réel deI, etCfsa courbe représentative

dans un repère du plan. L"équation réduite de la tangente à la courbeCfau pointAd"abscisseaest : y=f?(a)×(x-a)+f(a)

EXEMPLE

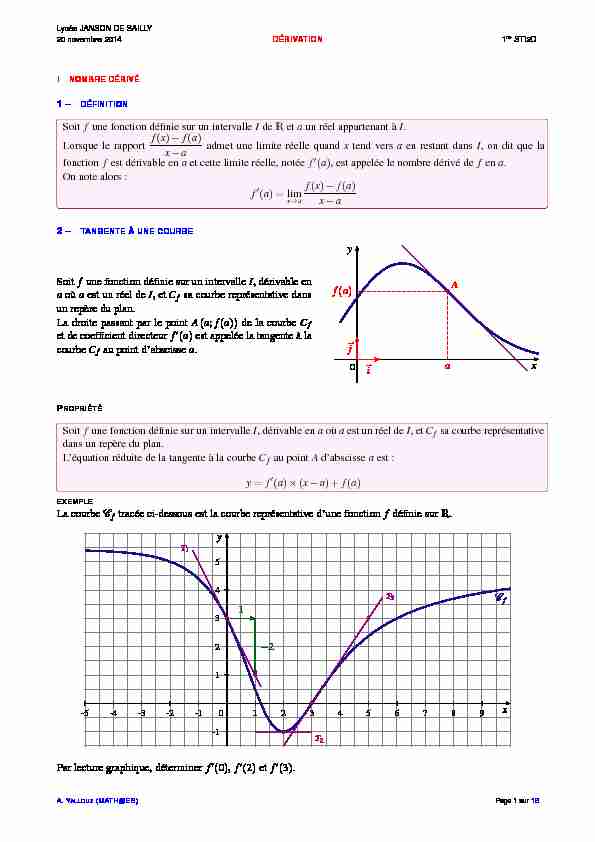
La courbeCftracée ci-dessous est la courbe représentative d"une fonctionfdéfinie surR. 12345
-1

1 2 3 4 5 6 7 8 9-1-2-3-4-50xy

1 -2 Cf T1 T 3 T 2 Par lecture graphique, déterminerf?(0),f?(2)etf?(3).

A. YALLOUZ(MATH@ES)Page 1 sur16

Lycée JANSON DE SAILLY20 novembre 2014

DÉRIVATION1reSTI2D

1. Le nombre dérivéf?(0)est égal au coefficient directeur de la tangenteT1à la courbeCfau point d"abscisse

0. Par lecture graphique, le coefficient directeur de la droiteT1est égal à-2. Ainsi,f?(0) =-2

2. La tangenteT2à la courbeCfau point d"abscisse 2 est parallèle à l"axe des abscisses. Doncf?(2) =0

3. La droiteT3, tangente à la courbeCfau point d"abscisse 3 passe par les points de coordonnées(3;0)et

(5;3). Son coefficient directeuraest a=3-0

5-3=32

Le nombre dérivéf?(3)est égal au coefficient directeur de la tangente à la courbeCfau point d"abscisse 3.

Doncf?(3) =3

2

REMARQUE

La courbe représentative d"une fonctionfpeut avoir une tangente en un pointasans que la fonction soit

dérivable ena. La courbe représentative de la fonction racine carrée est tangente à la droite d"équationx=0 en 0. Or la fonction racine carrée n"est pas dérivable en 0 en effet: lim x→0⎷ x-⎷0 x-0=limx→0⎷ x x=limx→01⎷x= +∞ ce n"est pas une limite finie donc la fonction racine carrée n"est pas dérivable en 0.

0xy?i?

j

II FONCTION DÉRIVÉE

1 -DÉFINITION

Soitfune fonction définie sur un intervalleIdeR. Lorsque pour tout réelxappartenant àI,fest dérivable enx, on dit quefest dérivable surI.

La fonction qui associe à tout réelxappartenant àIson nombre dérivéf?(x)est appelée la fonction dérivée de

fsur l"intervalleI. Elle est notéef?.

2 -DÉRIVÉES DES FONCTIONS DE RÉFÉRENCE

fonction définie et dérivable sur :fonctionfdéfinie par :fonction dérivéef?définie par :

Rf(x) =kf?(x) =0

Rf(x) =ax+ba

Rf(x) =xn(nentiern?1)f?(x) =nxn-1

]-∞;0[ou]0;+∞[f(x) =1xf?(x) =-1x2 ]-∞;0[ou]0;+∞[f(x) =1xn(nentiern?1)f?(x) =-nxn+1 ]0;+∞[f(x) =⎷xf?(x) =12⎷x

Rf(x) =sinxf?(x) =cosx

Rf(x) =cosxf?(x) =-sinx

A. YALLOUZ(MATH@ES)Page 2 sur16

Lycée JANSON DE SAILLY20 novembre 2014

DÉRIVATION1reSTI2D

3 -DÉRIVÉES ET OPÉRATIONS

uetvsont deux fonctions dérivables sur un intervalleI fonctionfdéfinie par :fonction dérivéef?:

Produit d"une fonction par un réelkkuku?

Sommeu+vu?+v?

Produitu×vu?v+uv?

Quotient (v?=0 surI)u

v u?v-uv? v2

Inverse (v?=0 surI)1

v-v?v2 Composée avec une fonction circulairesin(u)u?×cos(u) cos(u)-u?×sin(u)

EXEMPLES

1.Produit de deux fonctionsSoitfla fonction définie sur]0;+∞[parf(x) =?

2+x2 3?? 1-2x? . Calculerf?(x). Sur]0;+∞[fest dérivable comme produit de deux fonctions dérivables. f=uvd"oùf?=u?v+uv?. Avec pour tout réelxappartenant à l"intervalle]0;+∞[, u(x) =2+x2

3d"oùu?(x) =2x3

v(x) =1-2 xd"oùv?(x) =2x2 Soit pour tout réelxappartenant à l"intervalle]0;+∞[, f ?(x) =2x

3×?

1-2x? +2x2×?

2+x23?

2x

3-43+4x2+23

2x3-2x2+6

3x2 Ainsi,f?est la fonction définie sur]0;+∞[parf?(x) =2x3-2x2+6 3x2.

2.Quotient de deux fonctionsSoitfla fonction définie surRparf(x) =4x-3

x2+1. Calculerf?(x). SurR,fest dérivable comme somme et quotient de deux fonctions dérivables. f=u vd"oùf?=u?v-uv?v2. Avec pour tout réelx, u(x) =4x-3 d"oùu?(x) =4 v(x) =x2+1 d"oùv?(x) =2x

A. YALLOUZ(MATH@ES)Page 3 sur16

Lycée JANSON DE SAILLY20 novembre 2014

DÉRIVATION1reSTI2D

Soit pour tout réelx,

f ?(x) =4(x2+1)-2x(4x-3) (x2+1)2

4x2+4-8x2+6x

(x2+1)2 -4x2+6x+4 (x2+1)2 Ainsi,f?est la fonction définie surRparf?(x) =-4x2+6x+4 (x2+1)2.

3. Une particule est animée d"un mouvement rectiligne sinusoïdal d"équationy(t) =0,08sin(12t+0,3)oùy(t)

est en mètres etten secondes. La vitesse instantanéev(t)est donnée pary?(t)soit v(t) =0,08×12×cos(12t+0,3) =0,96cos(12t+0,3)

III DÉRIVÉE ET VARIATIONS D"UNE FONCTION

1 -THÉORÈME1

Soitfune fonction dérivable et monotone sur un intervalleIdeR. — Sifest constante surI, alors pour tout réelxappartenant àI,f?(x) =0. — Sifest croissante surI, alors pour tout réelxappartenant àI,f?(x)?0. — Sifest décroissante surI, alors pour tout réelxappartenant àI,f?(x)?0.

Le théorème suivant, permet de déterminer les variations d"une fonction sur un intervalle suivant le signe de sa

dérivée.

2 -THÉORÈME2

Soitfune fonction dérivable sur un intervalleIdeRetf?la dérivée defsurI. — Sif?est nulle surI, alorsfest constante surI.

— Sif?est strictement positive surI, sauf éventuellement en un nombre fini de points où elle s"annule, alors

fest strictement croissante surI.

— Sif?est strictement négative surI, sauf éventuellement en un nombre fini de points où elle s"annule, alors

fest strictement décroissante surI.

3 -THÉORÈME3

Soitfune fonction dérivable sur un intervalle ouvertIdeRetx0un réel appartenant àI.

1. Sifadmet un extremum local enx0, alorsf?(x0) =0.

2. Si la dérivéef?s"annule enx0en changeant de signe, alorsfadmet un extremum local enx0.

x ax0b f ?(x)-|0|+ f(x) minimumx ax0b f ?(x)+|0|- f(x)maximum

A. YALLOUZ(MATH@ES)Page 4 sur16

Lycée JANSON DE SAILLY20 novembre 2014

DÉRIVATION1reSTI2D

REMARQUES

1. Dans la proposition 2. du théorème 3 l"hypothèseen changeant de signeest importante.

Considérons la fonction cube définie surRparf(x) =x3qui a pour dérivée la fonction f ?définie surRparf?(x) =3x2. f ?(0) =0 et pour tout réelxnon nul,f?(x)>0. La fonction cube est strictement croissante surRet n"admet pas d"extremum en 0. 0xy

2. Une fonction peut admettre un extremum local enx0sans être nécessairement dérivable.

Considérons la fonctionfdéfinie surRparf(x) =|x-1|+1 . fest une fonction affine par morceaux,fadmet un minimumf(1) =1 orfn"est pas dérivable en 1. 0xy

POINT MÉTHODE

En pratique, pour étudier les variations d"une fonctionfdérivable sur son ensemble de définitionDf:

— on détermine la dérivéef?def;

— on étudie le signe def?surDf;

— on applique le théorème 2 sur chacun des intervalles deDfoù le signe def?est constant;

— on dresse le tableau des variations en indiquant les extremums, s"il y a lieu et éventuellement les limites

aux bornes de son ensemble de définition.

EXEMPLE:ÉTUDE D"UNE FONCTION

Soitfla fonction définie surRparf(x) =4x-3

x2+1.

1. Calculerf?(x).

SurRfest dérivable comme somme et quotient de deux fonctions dérivables. f=u vd"oùf?=u?v-uv?v2. Avec pour tout réelx, u(x) =4x-3 d"oùu?(x) =4 v(x) =x2+1 d"oùv?(x) =2x

Soit pour tout réelx,

f ?(x) =4(x2+1)-2x(4x-3) (x2+1)2

4x2+4-8x2+6x

(x2+1)2 -4x2+6x+4 (x2+1)2 Ainsi,f?est la fonction définie surRparf?(x) =-4x2+6x+4(x2+1)2

A. YALLOUZ(MATH@ES)Page 5 sur16

Lycée JANSON DE SAILLY20 novembre 2014

DÉRIVATION1reSTI2D

2. Étudier les variations de la fonctionf

Les variations de la fonctionfse déduisent du signe de sa dérivée.

Étudions le signe def?(x) =-4x2+6x+4

(x2+1)2:

Pour tout réelx,(x2+1)2>0. Par conséquent,f?(x)est du même signe que le polynôme du second degré

-4x2+6x+4 aveca=-4,b=6 etc=4.

Le discriminant du trinôme estΔ=b2-4acSoit

Δ=62-4×4×(-4) =100

CommeΔ>0, le trinôme admet deux racines :

x

1=-b-⎷

2aSoitx1=-6-10-8=2

etx2=-b+⎷

2aSoitx2=-6+10-8=-12

Un polynôme du second degré est du signe deasauf pour les valeurs comprises entre les racines.

Nous pouvons déduire le tableau du signe def?(x)suivant les valeurs du réelxainsi que les variations de la

fonctionf: x-∞-122+∞ f ?(x)- 0+0- f(x) -41

A. YALLOUZ(MATH@ES)Page 6 sur16

Lycée JANSON DE SAILLY20 novembre 2014

DÉRIVATION1reSTI2D

EXERCICE 1

La courbeCfci-dessous est la représentation graphique d"une fonctionfdéfinie surRdans un repère du plan.

On notef?la fonction dérivée def.

La courbeCfvérifie les propriétés suivantes : — La tangente à la courbeCfau pointAd"abscisse-2 est parallèle à l"axe des abscisses ; — la tangente à la courbeCfau pointB(0;2)passe par le point de coordonnées(2;0). 1234
-1 -2

1 2 3 4-1-2-3-40xyCfA

B

Donner les valeurs def(-2),f?(-2)etf?(0).

EXERCICE 2

Sur la figure ci-dessous les droitesd1,d2,d3etd4sont tangentes à la courbeCfreprésentative d"une fonction

fdérivable surR. 123
-1 -2 -3

1 2 3 4 5 6 7 8 9-1-2-3-40xy

Cf d 1 d2 d3 d4

1. Déterminer graphiquementf(0),f(2),f(4)etf(8).

2. Déterminer graphiquement les nombres dérivésf?(0),f?(2),f?(4)etf?(8).

3. En déduire les équations réduites des tangentesd1,d2,d3etd4.

EXERCICE 3

Sur la figure ci-dessous,Cfest la courbe représentative d"une fonctionfdérivable surR. Les droitesd1,d2,

d

3etd4sont tangentes à la courbeCf.

A. YALLOUZ(MATH@ES)Page 7 sur16

Lycée JANSON DE SAILLY20 novembre 2014

DÉRIVATION1reSTI2D

1234567

-1 -2 -3 -4

1 2 3 4 5 6-1-2-3-4-5-6-7-80xy

d1d 2 d 3d 4 Cf BA

1. Déterminer graphiquementf(-4),f(-2)etf(2).

2. Déterminer graphiquement les nombres dérivésf?(-4)etf?(2).

3. La tangente à la courbeCfau pointAd"abscisse-2 passe par l"origine du repère. Déterminerf?(-2).

4. La tangenteTà la courbeCfau pointB?

quotesdbs_dbs33.pdfusesText_39

[PDF] primitive terminale sti2d

[PDF] tableau dérivée sti2d

[PDF] calcul primitive ti 82

[PDF] ti 89 probabilité

[PDF] loi normale ti 89

[PDF] equation differentielle t.i 89

[PDF] règle de dérivation

[PDF] fonction valeur absolue dérivable en 0

[PDF] primitive valeur absolue

[PDF] dérivation linguistique

[PDF] dérivation définition

[PDF] le dernier jour d'un condamné analyse chapitre par chapitre

[PDF] le dernier jour dun condamné résumé chapitre par chapitre en arabe

[PDF] le dernier jour dun condamné séquence pédagogique pdf

[PDF] anaphore dans le dernier jour dun condamné