[PDF] DS 8 : Electromagnétisme 3 avr. 2019 Un signal

View - Download DS 8 : Electromagnétisme

Previous PDF

Next PDF

PT Lycée Benjamin Franklin m ercredi 3 avril 2019 DS 8 : Electromagnétisme (4 heures sans calculette) PREMIERE PARTIE Champ E créé par une couche cylindrique Tournez la page S.V.P.Tournez la page S.V.P.

DEUXIÈME PARTIE Cable coaxial EXERCICE 6 : Effet de peau EXERCICE 7 : Cable coaxial (CCP PSI 2011) 2/12

Un signal qui se propage dans un câble coaxial peut subir plusieurs modifications. Il peut

être déformé (milieu dispersif), atténué (milieu dissipatif). Il peut aussi subir des réflexions au

niveau des connexions.

Ce sujet aborde la modélisation du câble coaxial et les phénomènes de réflexion d'ondes lorsque le

câble est connecté sur une charge. Un câble coax ial est formé de deux très bons conducteurs, de même l ongueu r l, l'un entourant l'autre. L'un est un conducteur massif de rayon R 1 , appelé l'âme du conducteur. L'autre est un conducteur cylindrique creux de rayon intérieur R 2 et de rayon extérieur R 3 , appelé la gaine du conducteur. L'espace inter-conducteur comporte un isolant.

On a : R

1 = 0,25 mm, R 2 = 1,25 mm et l = 100 m.

I] Modélisation :

Dans la mesure où les champs électromagnétiques ne pénètrent pas dans les conducteurs

parfaits, on assimilera le câble coaxial à deux surfac es parfaite ment conductrices, cylindriques,

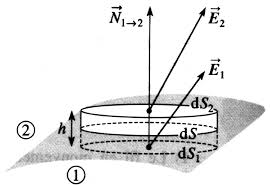
coaxiales. Le conducteur (1) a un rayon R 1 , le conducteur (2) a un rayon R 2 (figure 1). Ces deux conducteurs ont même longueur l. Vu que l >> R 2 , on négligera les effets de bord. L'espace entre les conducteurs sera assimilé au vide sauf explicitation contraire.

Figure 1 : Portion de câble

On note (,,)

rz uuu la base en coordonnées cylindriques.

Aucune connaissance particulière n'est requise pour la détermination de la capacité linéique

et de l'inductance linéique du câble.

A] Capacité linéique C :

On suppose ici que les conducteurs intérieur et extérieur portent les charges électrostatiques

respectives Q et - Q. Elles sont uniformément réparties en surface.

1)Ju stifier par des arguments d'invariance et de symétrie que ()

r EEru= dans l'espace inter- conducteur. R 2 R 1 z EXERCICE 6 : Effet de peau EXERCICE 7 : Cable coaxial (CCP PSI 2011) 2/12 Un signal qui se propage dans un câble coaxial peut subir plusieurs modifications. Il peut

être déformé (milieu dispersif), atténué (milieu dissipatif). Il peut aussi subir des réflexions au

niveau des connexions.

Ce sujet aborde la modélisation du câble coaxial et les phénomènes de réflexion d'ondes lorsque le

câble est connecté sur une charge. Un câble coax ial est formé de deux très bons conducteurs, de même l ongueu r l, l'un entourant l'autre. L'un est un conducteur massif de rayon R 1 , appelé l'âme du conducteur. L'autre est un conducteur cylindrique creux de rayon intérieur R 2 et de rayon extérieur R 3 , appelé la gaine du conducteur. L'espace inter-conducteur comporte un isolant.

On a : R

1 = 0,25 mm, R 2 = 1,25 mm et l = 100 m.

I] Modélisation :

Dans la mesure où les champs électromagnétiques ne pénètrent pas dans les conducteurs

parfaits, on assimilera le câble coaxial à deux surfac es parfaite ment conductrices, cylindriques,

coaxiales. Le conducteur (1) a un rayon R 1 , le conducteur (2) a un rayon R 2 (figure 1). Ces deux conducteurs ont même longueur l. Vu que l >> R 2 , on négligera les effets de bord. L'espace entre les conducteurs sera assimilé au vide sauf explicitation contraire.

Figure 1 : Portion de câble

On note (,,)

rz uuu la base en coordonnées cylindriques.

Aucune connaissance particulière n'est requise pour la détermination de la capacité linéique

et de l'inductance linéique du câble.

A] Capacité linéique C :

On suppose ici que les conducteurs intérieur et extérieur portent les charges électrostatiques

respectives Q et - Q. Elles sont uniformément réparties en surface.

1)Ju stifier par des arguments d'invariance et de symétrie que ()

r EEru= dans l'espace inter- conducteur. R 2 R 1 z 2/12 Un signal qui se propage dans un câble coaxial peut subir plusieurs modifications. Il peut

être déformé (milieu dispersif), atténué (milieu dissipatif). Il peut aussi subir des réflexions au

niveau des connexions.

Ce sujet aborde la modélisation du câble coaxial et les phénomènes de réflexion d'ondes lorsque le

câble est connecté sur une charge. Un câble coax ial est formé de deux très bons conducteurs, de même l ongueu r l, l'un entourant l'autre. L'un est un conducteur massif de rayon R 1 , appelé l'âme du conducteur. L'autre est un conducteur cylindrique creux de rayon intérieur R 2 et de rayon extérieur R 3 , appelé la gaine du conducteur. L'espace inter-conducteur comporte un isolant.

On a : R

1 = 0,25 mm, R 2 = 1,25 mm et l = 100 m.

I] Modélisation :

Dans la mesure où les champs électromagnétiques ne pénètrent pas dans les conducteurs

parfaits, on assimilera le câble coaxial à deux surfac es parfaite ment conductrices, cylindriques,

coaxiales. Le conducteur (1) a un rayon R 1 , le conducteur (2) a un rayon R 2 (figure 1). Ces deux conducteurs ont même longueur l. Vu que l >> R 2 , on négligera les effets de bord. L'espace entre les conducteurs sera assimilé au vide sauf explicitation contraire.

Figure 1 : Portion de câble

On note (,,)

rz uuu la base en coordonnées cylindriques.

Aucune connaissance particulière n'est requise pour la détermination de la capacité linéique

et de l'inductance linéique du câble.

A] Capacité linéique C :

On suppose ici que les conducteurs intérieur et extérieur portent les charges électrostatiques

respectives Q et - Q. Elles sont uniformément réparties en surface.

1)Ju stifier par des arguments d'invariance et de symétrie que ()

r EEru= dans l'espace inter- conducteur. R 2 R 1 z 3/12

2)Pour R

1 < r < R 2 , en utilisant le théorème de Gauss sur une surface que l'on précisera, exprimer ()Er en fonction de l, r, Q et 0

3)Le s conducteurs (1) et (2) sont portés aux potentiels respectifs V

1 et V 2 , constants. Par un calcul de circulation, exprimer V 1 -V 2 en fonction de Q, l, R 1 , R 2 et 0

4)On dé finit la capacité

l

Cdu câble de longueur l par

12 l Q C VV . Exprimer l

C en fonction

de l, R 1 , R 2 et 0 ε, puis la capacité linéique C du câble coaxial en fonction de R 1 , R 2 et 0

5)En pratique, l'espace inter-conducteur n'est pas du vide, mais comport e un isolant de

permittivité relative3,1 r

ε=. On a alors

0 2 1 2 ln() r C R R

Déterminer la valeur numérique de C.

B] Inductance linéique L :

On suppose ici que le câble coaxial est alimenté par un générateur de courant continu. Le

conducteur intérieur ass ure le transport du courant aller I 0 , le condu cteur extérieur assure le transport du courant retour -I 0 Les répartitions de ces courants sont superficielles et uniformes sur chaque conducteur. Pour le conducteur (1), on a une densité surfacique de courant : 1 0 1 2 sz I ju Rπ . On note : 2 s j la densité surfacique de courant sur le conducteur (2).

6)P réciser l'expression et l'unité de

2 s j

7)Il existe ent re les deux conducteurs un champ magnétique B

. Par des arg uments d'invariance et de symétrie, justifier que ()BBru

8)Pour R

1 < r < R 2 , par application du théorème d'Ampère sur un parcours que l'on précisera, exprimer B(r) en fonction I 0 , r et µ 0

9)On note :

2 0 2 m B w =, la densité volumique d'énergie magnétique. Par intégration sur le volume inter-conducteur, exprimer l'énergie magnétique W m du câble coaxial en fonction de I 0 0 , R 1 , R 2 et l.

10)On rappelle que

2 0 2 l m LI

W=. Exprimer l'inductance

l

L du câble de longueur l, en fonction

de µ 0 , R 1 , R 2 et de l.

11)En déduire l'inductance linéique L du câble coaxial en fonction de µ

0 , R 1 , R 2

Déterminer la valeur numérique de L.

3/12

2)Pour R

1 < r < R 2 , en utilisant le théorème de Gauss sur une surface que l'on précisera, exprimer ()Er en fonction de l, r, Q et 0

3)Le s conducteurs (1) et (2) sont portés aux potentiels respectifs V

1 et V 2 , constants. Par un calcul de circulation, exprimer V 1 -V 2 en fonction de Q, l, R 1 , R 2 et 0

4)On dé finit la capacité

l

Cdu câble de longueur l par

12 l Q C VV . Exprimer l

C en fonction

de l, R 1 , R 2 et 0 ε, puis la capacité linéique C du câble coaxial en fonction de R 1 , R 2 et 0

5)En pratique, l'espace inter-conducteur n'est pas du vide, mais comport e un isolant de

permittivité relative3,1 r

ε=. On a alors

0 2 1 2 ln() r C R R

Déterminer la valeur numérique de C.

B] Inductance linéique L :

On suppose ici que le câble coaxial est alimenté par un générateur de courant continu. Le

conducteur intérieur ass ure le transport du courant aller I 0 , le condu cteur extérieur assure le transport du courant retour -I 0 Les répartitions de ces courants sont superficielles et uniformes sur chaque conducteur. Pour le conducteur (1), on a une densité surfacique de courant : 1 0 1 2 sz I ju Rπ . On note : 2 s j la densité surfacique de courant sur le conducteur (2).

6)P réciser l'expression et l'unité de

2 s j

7)Il existe ent re les deux conducteurs un champ magnétique B

. Par des arg uments d'invariance et de symétrie, justifier que ()BBru

8)Pour R

1 < r < R 2 , par application du théorème d'Ampère sur un parcours que l'on précisera, exprimer B(r) en fonction I 0 , r et µ 0

9)On note :

2 0 2 m B w =, la densité volumique d'énergie magnétique. Par intégration sur le volume inter-conducteur, exprimer l'énergie magnétique W m du câble coaxial en fonction de I 0 0 , R 1 , R 2 et l.

10)On rappelle que

2 0 2 l m LI

W=. Exprimer l'inductance

l

L du câble de longueur l, en fonction

de µ 0 , R 1 , R 2 et de l.

11)En déduire l'inductance linéique L du câble coaxial en fonction de µ

0 , R 1 , R 2

Déterminer la valeur numérique de L.

4/12 II] Onde électromagnétique et impédance du câble coaxial : A] Détermination de l'onde électromagnétique :

On se place ici dans le cadre général de la théorie de l'électromagnétisme. On considère le

câble comme infini suivant l'axe des z. Une onde électromagnétique se propage à l'intérieur du

câble dans la région R 1 < r < R 2 , assimilable à du vide. Elle est définie par son champ électrique : (,,)cos() r

Erzttkzu

r où α est une constante positive.

On lui associe le champ électrique complexe :

jtkz r

Erzteu

r

On a : (,,)Re((, ,))ErztErzt=

où Re signifie partie réelle. De même, il existe un champ magnétique (,,)Brzt auquel on associe le champ complexe : (,,)Brzt , avec (,, )Re (( ,,)) BrztBrzt=

12)L'onde est-elle plane ? est-elle progressive ? Si oui, préciser sa direction de propagation.

13)On note E

0 l' amplitude maximale du champ électr ique dans le câble coaxial . Préciser l'unité de E 0 et exprimer (,,)Erzt en fonction de E 0 , r, z, k, ω, t et R 1

14)Rappeler les quatre équations de Maxwell dans le vide et préciser en quelques mots le

contenu physique de chacune d'elles.

15)A partir des équations de Max well, retr ouver l'équation de propagation vérifiée par le

quotesdbs_dbs22.pdfusesText_28

[PDF] Analyse technique du CAC 40 - Lobourse

[PDF] PRINCIPES ET DIRECTIVES REGISSANT LA CONDUITE

[PDF] principes et directives pour la gestion des risques microbiologiques

[PDF] Les personnages Candide - Le blog de Jocelyne Vilmin

[PDF] cach - English translation

[PDF] Déclaration de cession d 'un véhicule - Ville de Massy

[PDF] service du cadastre d 'accueil - ONIGT

[PDF] Algérie - Archives nationales

[PDF] trousse d 'évaluation du tdah de caddra - TDA/H Belgique

[PDF] Inventaire des symptômes du TDAH - Caddra

[PDF] SNAP - IV Échelle d 'évaluation pour le parent/professeur - Caddra

[PDF] CADDRA-Tableau des médicaments-Québec - Attention Deficit-Info

[PDF] Charges déductibles Mise ? jour mars 2015 - Deloitte

[PDF] LA CADES - Collectif pour un audit citoyen de la dette

[PDF] GUIDE pRATIQUE - FIDHorg