Tendance,stationnarité, autocovariance,opérateurretard

t) est un bruit blanc de variance ˙2 On a simul e trois trajectoires (A, B et C), et trac es trois fonctions d’autocorr elations (D, E et F) En d etaillant un peu, expliquer quel processus se cache derri ere chacune des gures 0 100 200 300 400 500-10-5 0 5 10 Serie A Index 0 100 200 300 400 500-2 0 2 4 Serie B Index 0 100 200 300 400 500

Renforcement S´eries Chronologiques - univ-toulouse

Feuille d’exercices n˚2 : Processus ARMA Exercice 1 Soit ηun bruit blanc et Xle ARMA(1,1) v´eriﬁant Xt − 2Xt−1 = ηt + 1 2 ηt−1 1 Quelle est la relation ARMA entre Xet son bruit blanc d’innovation ǫ? 2 Exprimez Xt en fonction des valeurs pass´ees de ǫ 3 Exprimez ǫt en fonction des valeurs pass´ees de X Exercice 2

M1 ISMAG MIS243Y - S´eries chronologiques

Corrig´e de l’examen de s´eries chronologiques du 5 juin 2006

n est un bruit blanc On peut donc tester l’ad´equation du mod`ele en calculant les autocorr´elations empiriques ρˆˆ n(j) des r´esidus ˆ k = X k − ˆa nX k−1 Pour qﬁx´e, ni trop grand ni trop petit, on pose T n = ρˆˆ n(1) + ··· + ρˆˆ n(q) Si le mod`ele est correct, T n suit approximativement la loi

SIGNAUX ALÉATOIRES

de signal aléatoire est appelé bruit blanc (au sens strict) 1En toute rigueur, il faudrait réserver le terme de covariance à la formule précédente appliquée à des signaux centrés, pour lesquels on a alors simplement une extension de la notion de variance d’une variable à deux variables aléatoires Il s’agit ici d’une fonction

Master 1 ESA Econométrie et Statistique Appliquée TD SERIES

tous significatifs avec l’hypothèse de bruit blanc pour les résidus, quel critère utilisez pour choisir le meilleur modèle parmi les trois [ AR(1), MA(1) et MA(2)] 10 Conclusion : Rappeler la méthodologie de Box-Jenkins pour l’identification et l’estimation des processus ARMA B)

Sujets des exercices - Site de Stéphane POUJOULY

Exercices corrigés pour travail personnel Q2 : On suppose que le bruit thermique est un bruit blanc dans une bande équivalente Beq=3GHz Que signifie

Tendance,stationnarité, autocovariance,opérateurretard

2/45 1 Tendance,stationnarité,autocovariance,opérateurretard temps température 1920 1925 1930 1935 1940 30 40 50 60 année passagers 1950 1952 1954 1956 1958 1960

COURS DE SERIES TEMPORELLES THEORIE ET APPLICATIONS

COURS DE SERIES TEMPORELLES THEORIE ET APPLICATIONS VOLUME 1 Introduction à la théorie des processus en temps discret Modèles ARIMA et méthode Box & Jenkins

[PDF] examen séries temporelles

[PDF] econometrie des series temporelles pdf

[PDF] économétrie des séries temporelles cours et exercices

[PDF] trucs et astuces un monde ? lire

[PDF] le paysage dans le cadre des portières

[PDF] correction bac francais 2017

[PDF] série numérique cours exo7

[PDF] séries numériques exercices corrigés avec rappels cours

[PDF] série numérique exercices corrigés pdf

[PDF] cours series numeriques résumé pdf

[PDF] série numérique convergence

[PDF] séries numériques l2

[PDF] serie de bertrand exercice corrigé

[PDF] série ln(n)/n

[PDF] série numérique exo7 cours

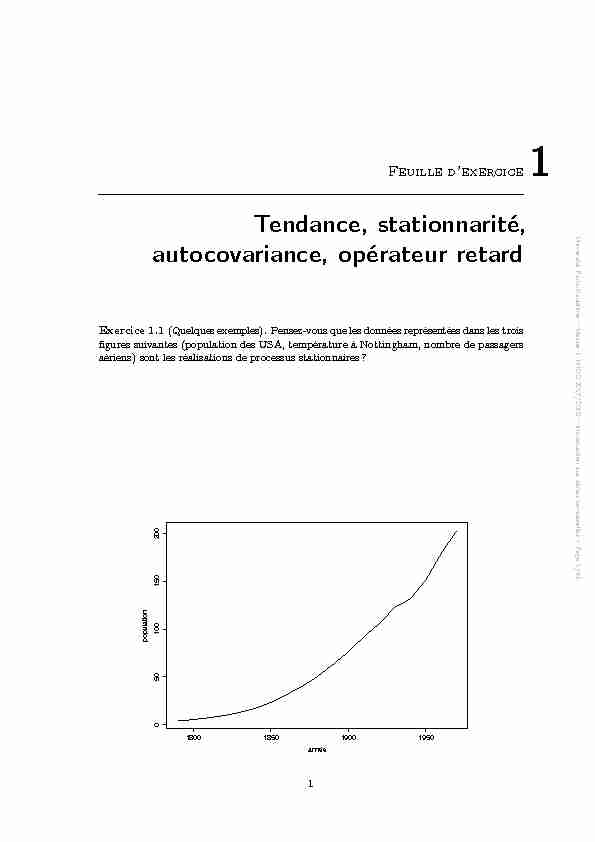Tendance,stationnarité, autocovariance,opérateurretard

Tendance,stationnarité, autocovariance,opérateurretard

année population

1800185019001950

0 50
100
150
200
temps température

1920 1925 1930 1935 1940

30 40 50 60

année passagers

195019521954195619581960

100
200
300
400
500
600

Ƕ Ƕ 1

`1 X

N(0;1) Y=XU=1XU=0ɍU

ĕ1/2 X

XY ā

(X;Y) = 0 XY

P(Y2I) =P(X2I)1

2+P(X2I)1

2=P(X2I)X=X

(X;Y) =E(XY) =E(X2)E(U=1)E(X2)E(U=0) = 0 (YjX=x) =1

2(x+x)6=(Y)XY

X0=XXt="tXt6= 0 ɍ ("t)t6=0 P("t=

1) = 1/2 X (Xt) = 0(Xt) = 1 t

s6=t s6= 0t6= 0(Xs;Xt) =E(X2)E("s)E("t) = 0 s= 0 t= 0 Ƕĕ ĕ (Xs;Xt) = 0

X= (Xt)t2N

Xt=+Xt1+Zt t1 ɍX0= 0 ɍ(Zt)t2N

XX X (Xt)t2N t0 Xt=t+Z1++Zt=t+StǶɍE(Xt) =t st X(t;t+h) =E((Xtt)(Xt+h(t+h))) =E(St(St+S0h)) =E(S2t) =2t t ā = 0 Ƕ

Xt=XtXt1=+Zt

X= (Xt)t2ZY= (Yt)t2Z Ƕ (Xt;Ys) = 0 s;t

Z= (Zt)t2Z Zt=Xt+Yt t2Z

X Y

ǶZ=X+Y

Z(t;t+h) =

X(t;t+h)+

Y(t;t+h)+(Xt;Yt+h)+(Yt;Xt+h) =

x(h)+ Y(h) t Z

Xt=Ztt Xt=Zt+ 1t (Zt)t2Z

Xt=Z1++Ztɍ(Zt)t2Z

Xt=Zt+Zt1 ɍ(Zt)t2Z 2R

Xt=ZtZt1ɍ(Zt)t2Z

Yt= (1)tZtXt=Yt+Ztɍ(Zt)t2Z

X(t;t+h) =E((Z1++Zt)2) =2t t

(1)X= 0

X(t;t+h) =2(1 +2)h=0+2jhj=1

X= 0

X(t;t+h) =4h=0

Xt= 2ZttǶɍ (Xt) = 42t

X= (Xt)t2Z

t2ZXt=A(t)+B(t)ɍAB

2 ɍ2R X

X(t) =E(A)(t) +E(B)(t) = 0

X(t;t+h) =E(A2)(t)((t+h)) +E(B2)(t)((t+h)) +

=0z}|{ E(AB) =2Re(iti(t+h)) =2Re(ih) =2(h) t ĕ :Z!RǶ (0) = 1 (h) =jhj= 1 (h) = 0

Ƕ jj 1/2

(h) = 1h= 0 (h) = 1/hh6= 0 (h) = 1 +(h/2) (h) = (1)jhj (h) =(Xh;X0) =(X0;Xh) = (h) n1v2Rn (hv; nvi=)X 1j;kn vj (kj)vk=X 1j;kn (vjXj;vkXk) = 0 nX j=1 vjXj 1 A0; n0 n= ( (jk))1j;kn= 0 BBBB@ 1 1 1

[PDF] Tendance,stationnarité, autocovariance,opérateurretard