FONCTION LOGARITHME NÉPÉRIEN









FONCTION LOGARITHME NEPERIEN

La fonction logarithme népérien notée ln
LogTS


Exponentielle et logarithme

La fonction exponentielle (de base e) et la fonction logarithme (népérien) sont des fonctions réciproques : leurs courbes.
exponentielle et logarithme


La fonction logarithme décimal

La fonction logarithme décimal. Propriétés analytiques. Pour x strictement positif log(x) = ln(x) ln(10). (avec ln(10) = 2
LogarithmeDecimal


FONCTION EXPONENTIELLE ET FONCTION LOGARITHME

Remarque : Cette formule permet de transformer une somme en produit et réciproquement. Corollaires : Pour tous réels x et y on a : a) exp(− ) =.
Texplog





FONCTION LOGARITHME DÉCIMAL

Remarque : La première formule permet de transformer un produit en somme. Ainsi celui qui aurait à effectuer 36 x 62
LogTT


Rappel mathématique

Le logarithme de x en base a est u (on écrit alors loga x = u). Une formule simple familière aux étudiants en finance
mathrappel


FONCTION LOGARITHME NEPERIEN (Partie 1)

La fonction logarithme népérien notée ln
LogTESL


Tableaux des dérivées et primitives et quelques formules en prime

%20d%C3%A9riv%C3%A9es





formulaire.pdf

de définition de la formule : par exemple √a sous-entend a 李 0 n ∈ N∗
formulaire


FONCTION LOGARITHME NÉPÉRIEN

La fonction logarithme népérien notée ln
LogTC


212897 FONCTION LOGARITHME NÉPÉRIEN 1 YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr

FONCTION LOGARITHME NÉPÉRIEN

Tout le cours en vidéo : https://youtu.be/VJns0RfVWGg En 1614, un mathématicien écossais, John Napier (1550 ; 1617) ci-contre, plus connu sous le nom francisé de Neper publie " Mirifici logarithmorum canonis descriptio ». Dans cet ouvrage, qui est la finalité d'un travail de 20 ans, Neper présente un outil permettant de simplifier les calculs opératoires : le logarithme. Neper construit le mot à partir des mots grecs " logos » (logique) et arithmos (nombre). Toutefois cet outil ne trouvera son essor qu'après la mort de Neper. Les mathématiciens anglais Henri Briggs (1561 ; 1630) et William Oughtred (1574 ;

1660) reprennent et prolongent les travaux de Neper.

Les mathématiciens de l'époque établissent alors des tables de logarithmes de plus en plus précises.

L'intérêt d'établir ces tables logarithmiques est de permettre de substituer une multiplication par une addition

(Partie 3). Ceci peut paraître dérisoire aujourd'hui, mais il faut comprendre qu'à cette époque, les calculatrices

n'existent évidemment pas, les nombres décimaux ne sont pas d'usage courant et les opérations posées telles

que nous les utilisons ne sont pas encore connues. Et pourtant l'astronomie, la navigation ou le commerce

demandent d'effectuer des opérations de plus en plus complexes.

Partie 1 : Fonction réciproque

Exemple :

Dire que 9 est l'image de 3 par la fonction carré, revient à dire que 3 est l'image de 9 par la

fonction racine carrée.

On note : 3

=9⟺ 9=3.

On a également : 5

=25⟺ 25=5.
De façon générale, pour tout réel et positifs, on a :

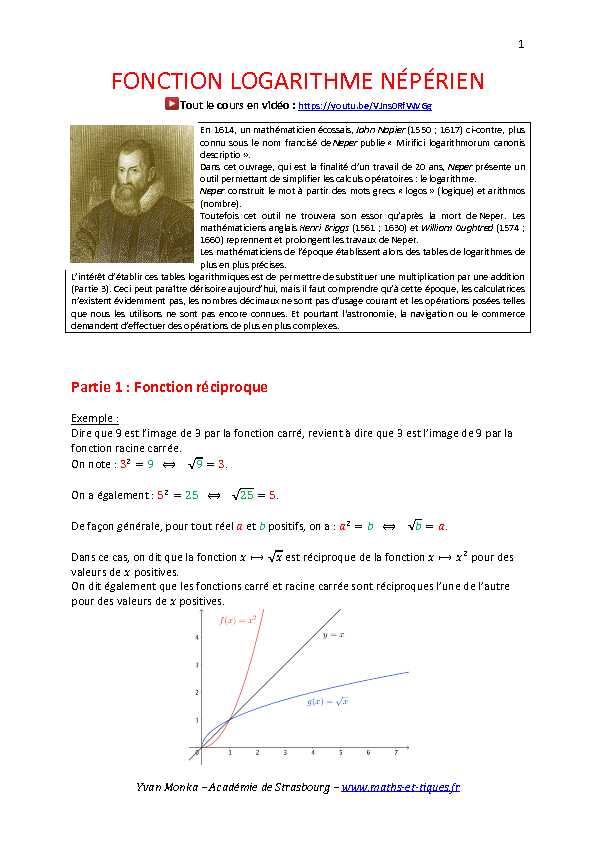
Dans ce cas, on dit que la fonction ⟼

est réciproque de la fonction ⟼ pour des valeurs de positives.

On dit également que les fonctions carré et racine carrée sont réciproques l'une de l'autre

pour des valeurs de positives. 2 YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr

Les courbes représentatives des fonctions carré et racine carrée sont symétrique l'une de

l'autre par rapport à la droite d'équation = pour des valeurs de positives. Définition : Soit une fonction continue et strictement monotone sur un intervalle.

On appelle fonction réciproque de , la fonction telle que : )=⟺)=.

Propriété : Les courbes représentatives de deux fonctions réciproques sont symétriques

l'une de l'autre par rapport à la droite d'équation =. Méthode : Déterminer la fonction réciproque d'une fonction

Vidéo https://youtu.be/bgINubYekqo

Soit la fonction définie sur ℝ par =3-4. Déterminer la fonction réciproque de la fonction .

Correction

On pose :

Soit : 3-4=

3=+4

1 3 4 3 1 3 4 3

Soit encore :

= avec : 1 3 4 3 est la fonction réciproque de la fonction . Partie 2 : Fonction exponentielle et fonction logarithme

1) Rappels concernant la fonction exponentielle

Propriétés : La fonction exponentielle est définie, continue, dérivable, strictement croissante et convexe sur ℝ.

On a :

3 YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr

Propriétés :

=1 >0 , avec ∈ℕ

2) Définition de la fonction logarithme népérien

La fonction exponentielle est continue et strictement croissante sur ℝ, à valeurs dans

0;+∞

D'après le théorème des valeurs intermédiaires, pour tout réel de

0;+∞

l'équation = admet une unique solution dans ℝ.

Définitions : On appelle logarithme népérien d'un réel strictement positif , l'unique

solution de l'équation =. On la note ln. La fonction logarithme népérien, notée , est la fonction définie sur

0;+∞

, par ⟼ln)

Remarques :

- Les fonctions et sont réciproques l'une de l'autre.

1 2 0 2)

1 2 expln 4 YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr - Les courbes représentatives des fonctions et sont symétriques par rapport à la droite d'équation =.

A noter :

Dans le domaine scientifique, on utilise la fonction logarithme décimale, notée log, et définie par : log)= Propriétés de ln liées à la fontion exp : a) Pour >0 : = ⇔=ln) b) ln1)=0 ; ln)=1 ; lnL 1 M=-1 c) ln d) Pour >0 :

Démonstrations :

a) Par définition b) - =1 donc d'après a, on a : ln1)=0 = donc d'après a, on a : ln)=1 1 donc d'après a, on a : lnL 1 M=-1 c) Si on pose = , d'après a, on a : =ln)=ln d) Si on pose =ln), d'après a, on a : = Partie 3 : Propriétés de la fonction logarithme népérien

1) Relation fonctionnelle

Théorème : Pour tous réels et strictement positifs, on a : ln =ln)+ln)

Démonstration :

Donc : ln

=ln)+ln) 5 YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr Remarque : Voici comment Neper transformait un produit en somme : Celui qui aurait, par exemple, à effectuer 36×62, appliquerait la formule précédente, soit : log

36×62

=log 36
+log 62
≈1,5563+1,7924 (à, l'aide de la table ci-contre) L'addition étant beaucoup plus simple à effectuer que la multiplication, on trouve facilement : 36×62)≈3,3487 En cherchant à nouveau dans la table le logarithme égal à 3,3487, on trouve 2232, soit : 36×62=2232.

2) Conséquences

Corollaires : Pour tous réels et strictement positifs, on a : a) lnL 1

M=-ln)

b) lnL

M=ln)-ln)

c) lnU V= 1 2 ln) d) ln )=ln), avec entier relatif

Démonstrations :

a) lnL 1

M+ln)=lnL

1

×M=ln1)=0 donc lnL

1

M=-ln)

b) lnL

M=lnL×

1

M=ln)+lnL

1

M=ln)-ln)

c) 2lnU 1 YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr

FONCTION LOGARITHME NÉPÉRIEN

Tout le cours en vidéo : https://youtu.be/VJns0RfVWGg En 1614, un mathématicien écossais, John Napier (1550 ; 1617) ci-contre, plus connu sous le nom francisé de Neper publie " Mirifici logarithmorum canonis descriptio ». Dans cet ouvrage, qui est la finalité d'un travail de 20 ans, Neper présente un outil permettant de simplifier les calculs opératoires : le logarithme. Neper construit le mot à partir des mots grecs " logos » (logique) et arithmos (nombre). Toutefois cet outil ne trouvera son essor qu'après la mort de Neper. Les mathématiciens anglais Henri Briggs (1561 ; 1630) et William Oughtred (1574 ;

1660) reprennent et prolongent les travaux de Neper.

Les mathématiciens de l'époque établissent alors des tables de logarithmes de plus en plus précises.

L'intérêt d'établir ces tables logarithmiques est de permettre de substituer une multiplication par une addition

(Partie 3). Ceci peut paraître dérisoire aujourd'hui, mais il faut comprendre qu'à cette époque, les calculatrices

n'existent évidemment pas, les nombres décimaux ne sont pas d'usage courant et les opérations posées telles

que nous les utilisons ne sont pas encore connues. Et pourtant l'astronomie, la navigation ou le commerce

demandent d'effectuer des opérations de plus en plus complexes.

Partie 1 : Fonction réciproque

Exemple :

Dire que 9 est l'image de 3 par la fonction carré, revient à dire que 3 est l'image de 9 par la

fonction racine carrée.

On note : 3

=9⟺ 9=3.

On a également : 5

=25⟺ 25=5.
De façon générale, pour tout réel et positifs, on a :

Dans ce cas, on dit que la fonction ⟼

est réciproque de la fonction ⟼ pour des valeurs de positives.

On dit également que les fonctions carré et racine carrée sont réciproques l'une de l'autre

pour des valeurs de positives. 2 YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr

Les courbes représentatives des fonctions carré et racine carrée sont symétrique l'une de

l'autre par rapport à la droite d'équation = pour des valeurs de positives. Définition : Soit une fonction continue et strictement monotone sur un intervalle.

On appelle fonction réciproque de , la fonction telle que : )=⟺)=.

Propriété : Les courbes représentatives de deux fonctions réciproques sont symétriques

l'une de l'autre par rapport à la droite d'équation =. Méthode : Déterminer la fonction réciproque d'une fonction

Vidéo https://youtu.be/bgINubYekqo

Soit la fonction définie sur ℝ par =3-4. Déterminer la fonction réciproque de la fonction .

Correction

On pose :

Soit : 3-4=

3=+4

1 3 4 3 1 3 4 3

Soit encore :

= avec : 1 3 4 3 est la fonction réciproque de la fonction . Partie 2 : Fonction exponentielle et fonction logarithme

1) Rappels concernant la fonction exponentielle

Propriétés : La fonction exponentielle est définie, continue, dérivable, strictement croissante et convexe sur ℝ.

On a :

3 YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr

Propriétés :

=1 >0 , avec ∈ℕ

2) Définition de la fonction logarithme népérien

La fonction exponentielle est continue et strictement croissante sur ℝ, à valeurs dans

0;+∞

D'après le théorème des valeurs intermédiaires, pour tout réel de

0;+∞

l'équation = admet une unique solution dans ℝ.

Définitions : On appelle logarithme népérien d'un réel strictement positif , l'unique

solution de l'équation =. On la note ln. La fonction logarithme népérien, notée , est la fonction définie sur

0;+∞

, par ⟼ln)

Remarques :

- Les fonctions et sont réciproques l'une de l'autre.

1 2 0 2)

1 2 expln 4 YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr - Les courbes représentatives des fonctions et sont symétriques par rapport à la droite d'équation =.

A noter :

Dans le domaine scientifique, on utilise la fonction logarithme décimale, notée log, et définie par : log)= Propriétés de ln liées à la fontion exp : a) Pour >0 : = ⇔=ln) b) ln1)=0 ; ln)=1 ; lnL 1 M=-1 c) ln d) Pour >0 :

Démonstrations :

a) Par définition b) - =1 donc d'après a, on a : ln1)=0 = donc d'après a, on a : ln)=1 1 donc d'après a, on a : lnL 1 M=-1 c) Si on pose = , d'après a, on a : =ln)=ln d) Si on pose =ln), d'après a, on a : = Partie 3 : Propriétés de la fonction logarithme népérien

1) Relation fonctionnelle

Théorème : Pour tous réels et strictement positifs, on a : ln =ln)+ln)

Démonstration :

Donc : ln

=ln)+ln) 5 YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr Remarque : Voici comment Neper transformait un produit en somme : Celui qui aurait, par exemple, à effectuer 36×62, appliquerait la formule précédente, soit : log

36×62

=log 36
+log 62
≈1,5563+1,7924 (à, l'aide de la table ci-contre) L'addition étant beaucoup plus simple à effectuer que la multiplication, on trouve facilement : 36×62)≈3,3487 En cherchant à nouveau dans la table le logarithme égal à 3,3487, on trouve 2232, soit : 36×62=2232.

2) Conséquences

Corollaires : Pour tous réels et strictement positifs, on a : a) lnL 1

M=-ln)

b) lnL

M=ln)-ln)

c) lnU V= 1 2 ln) d) ln )=ln), avec entier relatif

Démonstrations :

a) lnL 1

M+ln)=lnL

1

×M=ln1)=0 donc lnL

1

M=-ln)

b) lnL

M=lnL×

1

M=ln)+lnL

1

M=ln)-ln)

c) 2lnU
12345 Next
  1. logarithme formule pdf
  2. logarithme formule changement base
  3. logarithme formule limites
  4. logarithme formule dérivée
  5. logarithme formule terminale
  6. formule logarithme népérien
  7. formule logarithme décimal
  8. formule logarithme et exponentielle