FONCTION LOGARITHME NEPERIEN
La fonction logarithme nÃĐpÃĐrien notÃĐe ln
LogTS
Exponentielle et logarithme
La fonction exponentielle (de base e) et la fonction logarithme (nÃĐpÃĐrien) sont des fonctions rÃĐciproques : leurs courbes.
exponentielle et logarithme
La fonction logarithme dÃĐcimal
La fonction logarithme dÃĐcimal. PropriÃĐtÃĐs analytiques. Pour x strictement positif log(x) = ln(x) ln(10). (avec ln(10) = 2
LogarithmeDecimal
FONCTION EXPONENTIELLE ET FONCTION LOGARITHME
Remarque : Cette formule permet de transformer une somme en produit et rÃĐciproquement. Corollaires : Pour tous rÃĐels x et y on a : a) exp(â ) =.
Texplog
FONCTION LOGARITHME DÃCIMAL
Remarque : La premiÃĻre formule permet de transformer un produit en somme. Ainsi celui qui aurait à effectuer 36 x 62
LogTT
Rappel mathÃĐmatique
Le logarithme de x en base a est u (on ÃĐcrit alors loga x = u). Une formule simple familiÃĻre aux ÃĐtudiants en finance
mathrappel
FONCTION LOGARITHME NEPERIEN (Partie 1)
La fonction logarithme nÃĐpÃĐrien notÃĐe ln
LogTESL
Tableaux des dÃĐrivÃĐes et primitives et quelques formules en prime
%20d%C3%A9riv%C3%A9es
formulaire.pdf
de dÃĐfinition de la formule : par exemple âa sous-entend a æ 0 n â Nâ
formulaire
FONCTION LOGARITHME NÃPÃRIEN
La fonction logarithme nÃĐpÃĐrien notÃĐe ln
LogTC
 1 YvanMonka-AcadÃĐmiedeStrasbourg-www.maths-et-tiques.fr
1 YvanMonka-AcadÃĐmiedeStrasbourg-www.maths-et-tiques.fr FONCTION LOGARITHME DÃCIMAL
En 1614, un mathÃĐmaticien ÃĐcossais, John Napier (1550 ; 1617) ci-contre, plus connu sous le nom francisÃĐ de Neper publie " Mirifici logarithmorum canonis descriptio Âŧ. Dans cet ouvrage, qui est la finalitÃĐ d'un travail de 20 ans, Neper prÃĐsente un outil permettant de simplifier les calculs opÃĐratoires : le logarithme. Neper construit le mot à partir des mots grecs " logos Âŧ (logique) et arithmos (nombre). Toutefois cet outil ne tr ouvera son essor qu'aprÃĻs la mort de Neper. Les mathÃĐmaticiens anglais Henri Briggs (1561 ; 1630) et William Oughtred (1574 ;1660) reprennent et prolongent les travaux de Neper.
Les mathÃĐmaticiens de l'ÃĐpoque ÃĐtablissent alors des tables de logarithmes de plus en plus prÃĐcises.L'intÃĐrÊt d'ÃĐtablir ces tables logarithmiques est de permettre de substituer une multiplication par une addition
(partie 2). Ceci peut paraÃŪtre dÃĐrisoire aujourd'hui, mais il faut comprendre qu'Ã cette ÃĐpoque, les calculatrices
n'existent ÃĐvidemment pas, les nombres dÃĐcimaux ne sont pas d'usage courant et les opÃĐrations posÃĐes telles
que nous les utilisons ne sont pas encore connues. Et pourtant l'astronomie, la navigation ou le commerce
demandent d'effectuer des opÃĐrations de plus en plus complexes. Partie 1 : Fonction exponentielle de base 10 et fonction logarithme dÃĐcimal1) DÃĐfinition
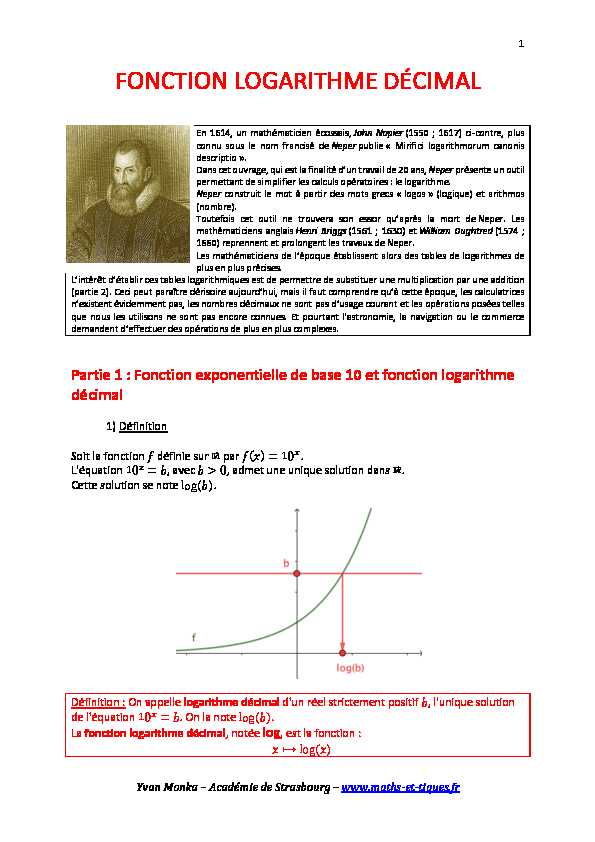
Soit la fonction í ĩ dÃĐfinie sur â par í ĩ =10L'ÃĐquation 10
=í ĩ, avec í ĩ>0, admet une unique solution dans â.Cette solution se note log(í ĩ).
DÃĐfinition : On appelle logarithme dÃĐcimal d'un rÃĐel strictement positif í ĩ, l'unique solution
de l'ÃĐquation 10 =í ĩ. On la note log(í ĩ). La fonction logarithme dÃĐcimal, notÃĐe log, est la fonction : í ĩâžlog(í ĩ) 2 YvanMonka-AcadÃĐmiedeStrasbourg-www.maths-et-tiques.frConsÃĐquences :
a) Pour í ĩ>0 : 10 =í ĩ revient à ÃĐcrire í ĩ=log(í ĩ) b) log10 c) Pour í ĩ>0 : 102) Sens de variation
PropriÃĐtÃĐ : La fonction logarithme dÃĐcimal í ĩâžlog(í ĩ) est croissante sur0;+â
Valeurs particuliÃĻres : log(1)=0 ; log(10)=1 ; log6 1 10 7=-1 Partie 2 : PropriÃĐtÃĐs de la fonction logarithme dÃĐcimal MÃĐthode : Simplifier une expression contenant des logarithmesVidÃĐo https://youtu.be/qdYQQlbz-AQ
Simplifier les expressions suivantes :
í ĩ=logí°ī2-2=+logí°ī2+
2= í ĩ=2log(í°ĩ)+log(2)-4log(í°ĩ)
í ĩ=log(10 1 5 DCorrection
í ĩ=logí°ī2-2=+logí°ī2+
2= =log6í°ī2-2=Ãí°ī2+
2=7 =log 4-2 =log(2) í ĩ=2log(í°ĩ)+log(2)-4log(í°ĩ) =log(í°ĩ )+log(2)-logPour a > 0 et b > 0 :
log =log(í ĩ)+log(í ĩ)Pour a > 0 et n entier naturel :
log(í ĩ )=í ĩlog(í ĩ) 3 YvanMonka-AcadÃĐmiedeStrasbourg-www.maths-et-tiques.fr =log(í°ĩÃ2)-log
=logíą 3 2 Ã2 3 4 I =log6 2 9 7 í ĩ=log(10 1 5 D =log(10 )-log(5) =í°ĩlog(10)-log(5) =í°ĩÃ1-log(5) =í°ĩ-log(5) Remarque : Voici comment Neper transformait un produit en somme : Celui qui aurait, par exemple, Ã effectuer í°ĩ6Ã62, appliquerait la formule prÃĐcÃĐdente, soit : 1 YvanMonka-AcadÃĐmiedeStrasbourg-www.maths-et-tiques.frFONCTION LOGARITHME DÃCIMAL
En 1614, un mathÃĐmaticien ÃĐcossais, John Napier (1550 ; 1617) ci-contre, plus connu sous le nom francisÃĐ de Neper publie " Mirifici logarithmorum canonis descriptio Âŧ. Dans cet ouvrage, qui est la finalitÃĐ d'un travail de 20 ans, Neper prÃĐsente un outil permettant de simplifier les calculs opÃĐratoires : le logarithme. Neper construit le mot à partir des mots grecs " logos Âŧ (logique) et arithmos (nombre). Toutefois cet outil ne tr ouvera son essor qu'aprÃĻs la mort de Neper. Les mathÃĐmaticiens anglais Henri Briggs (1561 ; 1630) et William Oughtred (1574 ;1660) reprennent et prolongent les travaux de Neper.
Les mathÃĐmaticiens de l'ÃĐpoque ÃĐtablissent alors des tables de logarithmes de plus en plus prÃĐcises.L'intÃĐrÊt d'ÃĐtablir ces tables logarithmiques est de permettre de substituer une multiplication par une addition
(partie 2). Ceci peut paraÃŪtre dÃĐrisoire aujourd'hui, mais il faut comprendre qu'Ã cette ÃĐpoque, les calculatrices
n'existent ÃĐvidemment pas, les nombres dÃĐcimaux ne sont pas d'usage courant et les opÃĐrations posÃĐes telles
que nous les utilisons ne sont pas encore connues. Et pourtant l'astronomie, la navigation ou le commerce
demandent d'effectuer des opÃĐrations de plus en plus complexes. Partie 1 : Fonction exponentielle de base 10 et fonction logarithme dÃĐcimal1) DÃĐfinition
Soit la fonction í ĩ dÃĐfinie sur â par í ĩ =10L'ÃĐquation 10
=í ĩ, avec í ĩ>0, admet une unique solution dans â.Cette solution se note log(í ĩ).
DÃĐfinition : On appelle logarithme dÃĐcimal d'un rÃĐel strictement positif í ĩ, l'unique solution
de l'ÃĐquation 10 =í ĩ. On la note log(í ĩ). La fonction logarithme dÃĐcimal, notÃĐe log, est la fonction : í ĩâžlog(í ĩ) 2 YvanMonka-AcadÃĐmiedeStrasbourg-www.maths-et-tiques.frConsÃĐquences :
a) Pour í ĩ>0 : 10 =í ĩ revient à ÃĐcrire í ĩ=log(í ĩ) b) log10 c) Pour í ĩ>0 : 102) Sens de variation
PropriÃĐtÃĐ : La fonction logarithme dÃĐcimal í ĩâžlog(í ĩ) est croissante sur0;+â
Valeurs particuliÃĻres : log(1)=0 ; log(10)=1 ; log6 1 10 7=-1 Partie 2 : PropriÃĐtÃĐs de la fonction logarithme dÃĐcimal MÃĐthode : Simplifier une expression contenant des logarithmesVidÃĐo https://youtu.be/qdYQQlbz-AQ
Simplifier les expressions suivantes :
í ĩ=logí°ī2-2=+logí°ī2+
2= í ĩ=2log(í°ĩ)+log(2)-4log(í°ĩ)
í ĩ=log(10 1 5 DCorrection
í ĩ=logí°ī2-2=+logí°ī2+
2= =log6í°ī2-2=Ãí°ī2+
2=7 =log 4-2 =log(2) í ĩ=2log(í°ĩ)+log(2)-4log(í°ĩ) =log(í°ĩ )+log(2)-logPour a > 0 et b > 0 :
log =log(í ĩ)+log(í ĩ)Pour a > 0 et n entier naturel :
log(í ĩ )=í ĩlog(í ĩ) 3 YvanMonka-AcadÃĐmiedeStrasbourg-www.maths-et-tiques.fr =log(í°ĩÃ2)-log
=logíą 3 2 Ã2 3 4 I =log6 2 9 7 í ĩ=log(10 1 5 D =log(10 )-log(5) =í°ĩlog(10)-log(5) =í°ĩÃ1-log(5) =í°ĩ-log(5) Remarque : Voici comment Neper transformait un produit en somme : Celui qui aurait, par exemple, Ã effectuer í°ĩ6Ã62, appliquerait la formule prÃĐcÃĐdente, soit :- logarithme formule pdf
- logarithme formule changement base
- logarithme formule limites
- logarithme formule dÃĐrivÃĐe
- logarithme formule terminale
- formule logarithme nÃĐpÃĐrien
- formule logarithme dÃĐcimal
- formule logarithme et exponentielle