 DE LA DILATATION DES TEMPS A LA CONTRACTION DES
DE LA DILATATION DES TEMPS A LA CONTRACTION DES
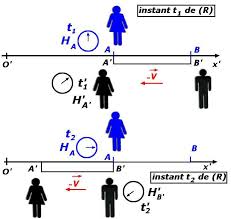
18 mars 2014 L est donc sa longueur propre. Cette règle est en mouvement à la vitesse V dans le référentiel (R') d'un observateur situé à l'origine O ...
 Chapitre 4.3 – La contraction des longueurs
Chapitre 4.3 – La contraction des longueurs
Situation : Le Bellatrix et l'Altaïr se croisent à une vitesse relative v. Question : Quelle est la longueur de l'Altaïr requise afin qu'Albert (A) et Archibald
 RELATIVITE RESTREINTE Introduction
RELATIVITE RESTREINTE Introduction
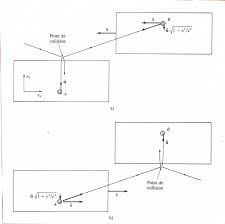
Figure VI : démonstration de la contraction de la longueur. VII. L'espace En ce sens la dilatation du temps et la contraction des longueurs se ...
 Corrigé du DM no4 – TS2 2013 Dilatation des durées & contraction
Corrigé du DM no4 – TS2 2013 Dilatation des durées & contraction
Comme démontré dans l'exercice précédent γ > 1 donc L2 > L1 : on a bien contraction des longueurs Démonstration ∆T′ = γ∆T0. Démonstration ∆T′ = γ∆T0.
 Relativité et électromagnétisme
Relativité et électromagnétisme
1) Contraction des longueurs . On peut aussi faire une demonstration thermodynamique de p = u. 3 . En effet la densité d'état d'un gaz de photons est : ρ(ϵ) ...
 LACONTRACTIONDETEXTE
LACONTRACTIONDETEXTE
contraction : d'une longueur de mille mots environ le texte fait l'objet d ➢ Intérêt argumentatif : impliquer le destinataire dans la démonstration qui va ...
 Chapitre 4.7 – La loi de Biot-Savart et le champ magnétique dun fil
Chapitre 4.7 – La loi de Biot-Savart et le champ magnétique dun fil
« contraction des longueurs » lorsqu'il y a des charges électriques en mouvement. Une démonstration faisant intervenir des principes avancés d' ...
 La Relativité restreinte expliquée aux enfants (de 7 à 107 ans)
La Relativité restreinte expliquée aux enfants (de 7 à 107 ans)
4 juil. 2007 Et je crois même que j'en connais une démonstration ! ... — C'est donc cela la contraction des longueurs dont mon prof de physique a parlé !
 La Relativité restreinte expliquée aux enfants (de 7 `a 107 ans)
La Relativité restreinte expliquée aux enfants (de 7 `a 107 ans)
2 juil. 2005 Et je crois même que j'en connais une démonstration ! ... — C'est donc cela la contraction des longueurs dont mon prof' de physique a parlé !
 RELATIVITE RESTREINTE Introduction
RELATIVITE RESTREINTE Introduction
Figure VI : démonstration de la contraction de la longueur. VII. L'espace-temps a quatre dimensions. Figure VII. Un passager dans un train roulant à grande
 Chapitre 4.3 – La contraction des longueurs
Chapitre 4.3 – La contraction des longueurs
Situation : Le Bellatrix et l'Altaïr se croisent à une vitesse relative v. Question : Quelle est la longueur de l'Altaïr requise afin qu'Albert (A) et Archibald
 DE LA DILATATION DES TEMPS A LA CONTRACTION DES
DE LA DILATATION DES TEMPS A LA CONTRACTION DES
18 mars 2014 L est donc sa longueur propre. Cette règle est en mouvement à la vitesse V dans le référentiel (R') d'un observateur situé à l'origine O ...
 Relativité restreinte
Relativité restreinte
des durées et de contractions des longueurs vues au I- comme le montre les A cause de la remarque Ž précédente la démonstration du théorème de ...
 Chapitre 10 : La relativité du temps
Chapitre 10 : La relativité du temps
1 août 2013 5.3 Contraction des longueurs . . . . . . . . . . . . . . . . . . . . . . . . . . 7. PAUL MILAN. 1. PHYSIQUE-CHIMIE. TERMINALE S ...
 Quelques aspects de la formulation initiale des transformations de
Quelques aspects de la formulation initiale des transformations de
15 janv. 2021 contraction des longueurs et la dilatation du temps seront les premiers ... B - Démonstration simple de la transformation de Lorentz sous sa ...
 Introduction à la RELATIVITE RESTREINTE
Introduction à la RELATIVITE RESTREINTE
servation de décalage correspond à une contraction de longueur selon le mouvement Démonstration : soit A'E symétrique de A'C' par rapport à A'B'.
 Introduction à la théorie des graphes
Introduction à la théorie des graphes
Longueur d'une chaîne : nombre des arêtes qui composent la chaîne. La démonstration fournit un algorithme de construction de cycle eulérien. Exemples.
 Relativité et électromagnétisme
Relativité et électromagnétisme
1) Contraction des longueurs . démonstration de la relation de réciprocité : si R/ se déplace par rapport `a R `a la vitesse v.
 Cours 9. Le quadri-vecteur énergie-impulsion
Cours 9. Le quadri-vecteur énergie-impulsion
Contraction des longueurs. Voir (Smith 1997
Relativite et electromagnetisme
Alain Comtet - alain.comtet@u-psud.fr, Universite Pierre et Marie Curie,Notes de Florian Bolgar
Table des matieres
1 Symetries et principe de relativite 5
I) Symetries et groupes de transformation . . . . . . . . . . . . . . . . . . . . 51) Changement de referentiels . . . . . . . . . . . . . . . . . . . . . . . .
52) Autres transformations . . . . . . . . . . . . . . . . . . . . . . . . . .
6 II) Relativite galileenne : . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 8 III) Principe de relativite . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 IV) Approfondissement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 132 Cinematique relativiste 14
I)Evenements . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .14 II) Diagrammes d'espace-temps . . . . . . . . . . . . . . . . . . . . . . . . . . . 15 III) Intervalle, invariance de l'intervalle . . . . . . . . . . . . . . . . . . . . . . . 16 IV) Classication des intervalles . . . . . . . . . . . . . . . . . . . . . . . . . . . 171) Intervalle de genre temps . . . . . . . . . . . . . . . . . . . . . . . . .
172) Intervalle de genre espace . . . . . . . . . . . . . . . . . . . . . . . .
183) Intervalle de genre lumiere . . . . . . . . . . . . . . . . . . . . . . . .
184) Structure causale de l'espace-temps . . . . . . . . . . . . . . . . . . .
18 V) Temps propre . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 193 Transformations de Lorentz 21
I) Transformations speciales de Lorentz . . . . . . . . . . . . . . . . . . . . . . 21II) Loi de composition des vitesses . . . . . . . . . . . . . . . . . . . . . . . . . 25
III) Consequences . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 25
1) Contraction des longueurs . . . . . . . . . . . . . . . . . . . . . . . .
252) Dilatation des temps . . . . . . . . . . . . . . . . . . . . . . . . . . .
263) Interpretation geometrique, diagramme de Minkowski . . . . . . . . .
26IV) Approfondissement . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 28
4 Groupe de Lorentz, formulation covariante 29
I) Elements de calcul tensoriel . . . . . . . . . . . . . . . . . . . . . . . . . . . 291) Scalaires . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
292) Vecteurs contravariants . . . . . . . . . . . . . . . . . . . . . . . . . .
302
3) Vecteurs covariants . . . . . . . . . . . . . . . . . . . . . . . . . . . .31
4) Contractions . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
325) Tenseurs . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
326) Espace euclidien en coordonnees cartesiennes . . . . . . . . . . . . . .
34II) Groupe de Lorentz . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35
1) Espace de Minkowski . . . . . . . . . . . . . . . . . . . . . . . . . . .
362) Illustrations . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
38III) Complements mathematiques . . . . . . . . . . . . . . . . . . . . . . . . . . 39
1) Groupe des rotations : . . . . . . . . . . . . . . . . . . . . . . . . . .
392) Groupe de Lorentz . . . . . . . . . . . . . . . . . . . . . . . . . . . .
413
1Sym etrieset princip ede relativit e
I)Sym etrieset group esde transformation
1)Changemen tde r eferentiels
La description d'une experience mettant en jeu un ensemble de particules en interac- tion necessite un observateur et un systeme de reference servant a indiquer la position des particules dans l'espace. Dans la plupart des situations que nous traiterons, ce systeme de referenceRsera constitue d'un triedre orthonormeOxyz. La m^eme experience peut ^etre analysee par rapport a un autre referentielR0attache au triedreO0x0y0z0. Exemples de referentiels : le wagon d'un train, une station spatiale en orbite autour de la terre etc... On va s'interesser a ce qui se passe si un observateur attache au referentielR0observe le m^eme phenomene. Si les equations du mouvement dansR0exprimees en termes des co- ordonnees (x0y0z0) ont la m^eme forme que dans le referentielR, on dira que la loi physique regissant le phenomene est invariante. Prenons l'exemple de deux particules en interaction par un potentiel centralV(j~x1~x2j) : m1d2~x1dt2=~r1V(j~x1~x2j)
m2d2~x2dt
2=~r2V(j~x1~x2j)(1.1)
SoitR0deduit deRpar une translationg1(~a). Les coordonnees des particules dansR0sont ~x01=g1(~a)~x1=~x1~aet~x02=g1(~a)~x2=~x2~a. Les equations du mouvement dansR0
s'ecrivent m1d2~x01dt
2=~r1V(j~x01~x02j)
m2d2~x02dt
2=~r2V(j~x01~x02j)(1.2)
Les equations gardent donc la m^eme forme.
Il est naturel de considerer un 3 eme observateur attache a un referentielR00. Pour passer du referentielRau referentielR00on est amene a composerg1avec une transformationg2 decrivant le passage du referentielR0au referentielR00. L'ensemble des transformations, muni de la loi de compositiong3=g2og1constitue un groupe (verier l'existence d'un element 4 neutre et d'un inverse) Dans le cas present, il s'agit du groupe des translations spatiales~x!~x0=~x~a. Chaque element du groupe depend de trois parametres. Le groupe des translations est un groupe continu a 3 parametres. De m^eme, si on eectue une rotation du referentiel independante du temps, les equations du mouvement vont garder la m^eme forme. Le groupe correspondant est le groupe des rota- tions engendre par les matrices orthogonales 33, groupe non-abelien a 3 parametres. Remarques :1) L'ensemble des transformations rotations et translations spatiales en- gendre un groupe a 6 parametres appele groupe euclidienE3deni par les transformations ~x!~x0=R~x~a(1.3) d'ou la loi de groupe (~a0;R0)(~a;R) = (~a0+R0~a;R0R) (1.4)2) Point de vue passif et actif
Les transformations de symetries peuvent ^etre consideres soit comme des transformations passives soit comme des transformations actives : Dans une transformation passive on decrit un m^eme phenomene physique dans deux referentiels distincts. Dans une transformation active on deplace le systeme physique en gardant le referentiel xe. Les solutions~x(t) et~x0(t) correspondent a deux evolutions physiques distinctes decrites dans le m^eme systeme de coordonnees. Le point de vue actif peut ^etre teste en laboratoire en faisant tourner les appareils. De m^eme l'ensemble du systeme solaire peut ^etre, par la pensee, transporte en un point quelconque de notre galaxie. On s'at- tend a observer les m^emes orbites et les m^emes periodes de revolution.3) Les transformations que nous venons de considerer re
etent des proprietes d'homogeneite et d'isotropie de l'espace physique.4) Le formalisme lagrangien permet de construire des equations covariantes vis a vis d'un
groupeGde transformations. Il sut pour cela de construire un lagrangien qui soit invariant sousG(a une derivee totale pres). On verie que L=12 (m1_~x12+m2_~x22)V(j~x1~x2j) (1.5) est invariant sousE3. 2)Autres transformations
Translations temporelles:t!t0=t+t0.
5 Transformations discretes :renversement du sens du temps :t!t0=tet parite : ~x! ~x. Cette derniere operation s'obtient en composant une re exion par rapport a un plan (par exemple par rapport au planxOy) avec une rotation ( d'angleautour deOz). Sous cette transformation~x!~x0=~x ~v!~v0=~v(1.6) On verie que la parite laisse invariante les equations de Newton.Qu'en est-il des lois de l'electromagnetisme?
Pour repondre a cette question, il faut specier comment se transforment les champselectrique et magnetique. Sous les transformations des champs ~E(~x;t)!~E0(~x0;t0) =~E(~x;t) ~B(~x;t)!~B(~x0;t) =~B(~x;t)(1.7) et des courants (~x;t)!0(~x0;t0) =(~x;t) ~j(~x;t)!~j0(~x0;t) =~j(~x;t)(1.8) on verie l'invariance des equations de Maxwell. Signalons que cette symetrie est mise en defaut dans les interactions faibles comme le montre l'experience de desintegrationde noyaux de cobalt. On prepare des atomes de cobalt dans un etat polarise, et on mesure le nombre d'electrons emis dans la directionpar rapport a l'axe de polarisation. En analysant l'image de cet evenement dans un miroir on verie que l'angle d'emission des electronsmesure par rapport a l'axe de polarisation devient. Si la parite est conserve, la probabilite d'^etre detecte endoit ^etre egale a celle d'^etre detectee en. L'experience montre que ce n'est pas le cas. Les interactions faibles ne sont donc pas invariantes sous la parite. Dilatations et transformations conformes :En general les lois de la physique ne sont pas invariantes par dilatation sauf dans quelques cas tres particuliers tel que celui celui de la physique statistique des systemes bi-dimensionnels au point critique. Dans ce cas on a inva- riance sous le groupe conforme. Rappelons qu'une transformation conforme est une bijection du plan sur lui m^eme qui preserve les angles. Si on posez=x+iy, une transformation conforme est caracterisee parz7!z0=f(z) avecfanalytique. On peut demontrer que lorsqu'on applique une transformation conforme a un mouve- ment brownien planaire~B(t) deni dans le domaineD, son imagef(~B(t)) a m^eme loi a un changement de temps pres et est donc encore une trajectoire brownienne dansf(D) . 6Figure1.1 { Violation de la parite
II)Relativit egalil eenne:
Nous venons de voir que les equations de la mecanique classique sont invariantes sous le groupe euclidien ~x7!~x0=R~x~a(1.9) Question : peut-on etendre ce groupe de symetries spatiales et donc purement geometriques a un groupe de transformations d'espace-temps? Pour cela il faut disposer non seulement de regles pour mesurer les longueurs mais aussi d'horloges pour mesurer le temps. On les suppose synchronisees et mesurant le m^eme temps absolu. On adjoint au groupe euclidien les transformations speciales de Galilee ~x7!~x0=~x~vt t7!t0=t(1.10) RetR0sont donc en translation rectiligne uniforme l'un par rapport a l'autre. On montre que les lois de la mecanique classique, en particulier l'equation de Newton m d2~xdt2=~F, sont invariantes sous ce groupe de transformations. Les referentiels correspondants
sont dits inertiels. Dans de tels referentiels le mouvement d'une particule libre ~F= 0 est rectiligne et uniforme. Toute deviation a la loi de Newton implique que le referentiel n'est pas inertiel. C'est notamment le cas du referentiel terrestre dans lequel les equations de la dynamique contiennent, outre la force~F, des forces ctives appelees forces d'inertie (force de Coriolis et force centrifuge). L'existence de referentiels d'inertie est un fait experimental. 7Figure1.2 { transformation de Galilee
L'ICRF (International Celestial Reference frame) sert actuellement de standard aupres des astronomes en matiere de referentiel inertiel. Centre au barycentre du systeme solaire, il est deni en mesurant avec precision les positions de sources extragalactiques . De maniere plus generale, le groupe de Galilee sera deni par les transformations de la forme :~x0=R~x~vt~a t0=t+t0(1.11)
Il s'agit donc d'un groupe a 10 parametres. SiRest un referentiel inertiel, alors tout referentielR0deduit deRpar une transformation de Galilee est aussi inertiel. Consequences et remarques :1) Le mouvement rectiligne uniforme est indecelable. Il est impossible par une experience locale de distinguer deux referentiels en translation rectiligne uniforme.2) Loi d'addition des vitesses : la transformation speciale de Galilee
~x0=~x~V t t0=t(1.12)
decrit le mouvement d'un referentielR0en translation rectiligne uniforme de vitesse~Vpar rapport au referentielR. Par derivation par rapport au temps on en deduit la loi d'addition des vitesses ~v0=~v~V(1.13)
III)Princip ede relativit e
Nous erigeons en principe les considerations precedentesExigeons que toutes les lois de la physique prennent la m^eme forme dans tous les referentiels
inertielsLes lois de la mecanique classique satisfont par construction le principe de relativite vis a
vis des transformations galileennes. 8 Qu'en est-il des interactions electromagnetiques decrites par les equations de Maxwell?8>>>><
>>>:div !E=0!rot!B00@!E@t
=0~j div!B= 0!rot!E+@!B@t = 0(1.14) La reponse n'est pas evidente. Il faut en eet se donner non seulement les lois de trans- formation des coordonnees mais aussi celles des champs. Montrons qu'il existe une version modiee des equations de Maxwell qui respecte l'invariance Galileenne. Elle est obtenue en supprimant le terme inductif @!B@t de la derniere equation. 8>>>< >>:div !E=0!rot!B00@!E@t
=0~j div!B= 0!rot!E= 0(1.15) Supposons que sous la transformation speciale de Galilee, ~x0=~x+~vt t0=t(1.16)
les observables physiques se transforment selon les transformations suivantes, 8>>>< >>:7!0(~x0;t0) =(~x;t) ~j(~x;t)7!~j0(~x0;t0) =~j(~x;t) +(~x;t)~v!E7!!E0=!E!B7!!B0(~x0;t0) =!B(~x;t) +~vc2^!E(~x;t)(1.17)
On peut verier que les grandeurs primees satisfont les equations de Maxwell modiees. Cependant, en supprimant ce terme inductif les equations precedentes ne peuvent pas decrire le phenomene de propagation de la lumiere! En eet, en introduisant les potentiels ~Aettels que~E=!ret~B=!rot!Ales equations deviennent respectivement : 00~j=!r(div!A)!A+1c
2!r@@t
(1.18) On ne voit pas apparaitre dans ces equations de terme de propagation. Revenons aux equations exactes et montrons qu'elles ne peuvent pas ^etre invariantes galileennes. Pour cela, on resoud les equations sans source en posant : (!B=!rot!A!E=@!A@t !r(1.19) 9Notons que les champs
!E;!Bsont invariants sous la transformation de jauge : (!A!!A+!r !@ @t (1.20)Les equations deviennent :
8<0+ div(@!A@t
0~j=!r(div!A)!A+1c
2 @2!A@t2+!r@@t
(1.21) On peut utiliser la liberte de jauge en se placant dans la jauge de Lorenz : div !A+1c 2@@t = 0 (1.22)Alors les equations prennent la forme :
8< 1c 2@2@t 2 0 1c 2@2@t2!A=0~j(1.23)
On verie que dans le vide, la premiere equation admet des solutions particulieres de la forme : (x;t) =F(x+ct) +G(xct) (1.24) Par consequent lesequations de Maxwell montrent qu'il existe des ondeselectromagnetiques se propageant a la vitessec=q100. Elles semblent ainsi suggerer l'existence d'un referentiel
inertiel privilegie. Dans tout autre referentiel, la vitesse de la lumiere devrait ^etre donnee par la loi de composition des vitesses. On devrait donc pouvoir mettre en evidence le mouvement de la terre par rapport a ce referentiel hypothetique. Aucune experience d'optique n'ayant permis de mettre en evidence le mouvement relatif de la terre par rapport a ce referentiel, il a fallu non seulement remettre en question l' existence d'un tel referentiel mais aussi renoncer aux transformations galileennes. Plusieurs approches complementaires ont ete developpees (voir J.B. Zuber, hep-th : 1307-quotesdbs_dbs50.pdfusesText_50[PDF] demonstration integrale nulle fonction nulle
[PDF] demonstration loi de reflexion
[PDF] démonstration mathématique 1+1=0
[PDF] démonstration nombre complexe z^n
[PDF] démonstration par récurrence d'une inégalité
[PDF] démonstration par récurrence exercices et problèmes
[PDF] démonstration par récurrence nombres complexes
[PDF] démonstration par récurrence terminale s
[PDF] démonstration somme suite géométrique
[PDF] démonstration théorème d'euler graphe
[PDF] demonstration z^n barre
[PDF] demontage banquette arriere peugeot 2008
[PDF] demontage thermomix 3000
[PDF] demontage thermomix tm21
