 Université Batna 2 - Faculté de Technologie 2021/2022 Corrigé-type
Université Batna 2 - Faculté de Technologie 2021/2022 Corrigé-type
Exercice 1: (6 points). 1. Le modèle d'un système peut être déterminé de Les points en commun entre la méthode de Strejc et la méthode de Broïda: ___ (2pts).
 EXERCICE IDENTIFICATION - CORRECTION - 1. gain statique K 2
EXERCICE IDENTIFICATION - CORRECTION - 1. gain statique K 2
EXERCICE IDENTIFICATION - CORRECTION -. 1. gain statique K. R. Y. M. K Paramètres du modèle de Strejc : A l'aide du nomogramme on trouve n=5
 Généralités 2- Identification en boucle ouverte 2.1 Méthodologie 2.2
Généralités 2- Identification en boucle ouverte 2.1 Méthodologie 2.2
2.1 Méthodologie. 2.2 Méthode directe : confrontation de la réponse théorique et expérimentale. 2.3 Méthode de Strejc. 2.4 Méthode de Broida. 2.5 Méthode rapide
 Identification des systèmes
Identification des systèmes
La méthode la plus connue est la méthode de Strejc. Le modèle est : H(p) trique du système corrigé. Dans ce qui suit et quels que soient vos résultats ...
 Plan du module
Plan du module
• Cours et exercices corrigés Collection Sciences Sup (IUT BTS Licence) Editeur Dunod • Méthode de Strejc (boucle ouverte : courbe en S) u. T a. T. Point d' ...
 Identification des Systèmes
Identification des Systèmes
Chap2 : METHODES DE BASE D'IDENTIFICATION. Chap.2/43. METHODE DE STREJC. ☞ Principe. ✓ La méthode d'identification de STREJC est basée sur les propriétés.
 Régulation industrielle A . Meghebbar. Série 01 M thodes dIde
Régulation industrielle A . Meghebbar. Série 01 M thodes dIde
Exercice 1. La po se à u helo e ou le ouve te d'u s st e est do Appliquer la méthode de Strejc pour identifier ce système selon une fonction de transfert en.
 Commande Linéaire Numérique. Travaux Pratiques
Commande Linéaire Numérique. Travaux Pratiques
6 de fev. de 2022 ➢ Exercice 1.2 Justifier par des calculs afférents la méthode de ... d'un système linéaire par la Méthode de Strejc. [40']. 1. Ouvrir un ...
 TD 1 : Modélisation des systèmes dynamiques
TD 1 : Modélisation des systèmes dynamiques
Exercice 5 (Modèles de Broïda et Strejc). La réponse indicielle unitaire d résonance ωR du système non corrigé). Exercice 22. Le lieu de Black d'un ...
 Identification des systèmes
Identification des systèmes
La méthode la plus connue est la méthode de Strejc. Le modèle est : 1 On se propose à travers cet exercice de déterminer une forme récursive de cette ...
 EXERCICE IDENTIFICATION - CORRECTION - 1. gain statique K 2
EXERCICE IDENTIFICATION - CORRECTION - 1. gain statique K 2
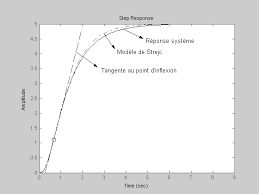
Modèle de Strejc. On choisit de considérer que le procédé ne possède pas de temps mort naturel. En traçant la tangente au point d'inflexion
 Sommaire
Sommaire
Méthode de Strejc sans intégrateur . Exemple 2 méthodes de Strejc et de Broïda en bf : . ... indicielle du SL que l'on doit modéliser et/ou corriger.
 Régulation industrielle A . Meghebbar. Série 01 M thodes dIde
Régulation industrielle A . Meghebbar. Série 01 M thodes dIde
3.1 Déterminer un modèle du système en BF méthode de Strejc toujours. Exercice 5 : Ide tifi atio d'u p o d e BF : dégazeur thermique.
 Généralités 2- Identification en boucle ouverte 2.1 Méthodologie 2.2
Généralités 2- Identification en boucle ouverte 2.1 Méthodologie 2.2
et expérimentale. 2.3 Méthode de Strejc. 2.4 Méthode de Broida. 2.5 Méthode rapide pour un procédé intégrateur. 3- Identification en boucle fermée.
 TD du CH24 : les correcteurs
TD du CH24 : les correcteurs
Exercice n°2 : comparaison des effets de différents correcteurs dans un système On désire adopter la méthode de Broïda pour régler le correcteur de cet.
 Identification des systèmes
Identification des systèmes
Table 2.5 Méthode de Strejc (système avec intégrateur) On se propose à travers cet exercice de déterminer une forme récursive de cette estimation.
 Asservissement des syst`emes linéaires `a temps continu Cours et
Asservissement des syst`emes linéaires `a temps continu Cours et
3.3 Méthodes de synth`ese . La méthode de Strejc permet d'identifier ce mod`eles `a partir de la réponse `a ... donné sous forme d'exercice corrigé.
 Commande des Machines
Commande des Machines
2.5.4 Méthode de Strejc . Exercice 2 (Fonctions de transfert d'un moteur `a courant continu) ... donné sous forme d'exercice corrigé.
 Identification des Systèmes
Identification des Systèmes
METHODE DE STREJC. ? Principe. ? La méthode d'identification de STREJC est basée sur les propriétés géométriques de la réponse indicielle d'un système
 Université Batna 2 - Faculté de Technologie 2021/2022 Corrigé-type
Université Batna 2 - Faculté de Technologie 2021/2022 Corrigé-type
Corrigé-type de l'Examen. Exercice 1: (6 points) Les points en commun entre la méthode de Strejc et la méthode de Broïda: ___ (2pts).
Asservissement des syst`emes
lin´eaires `a temps continuCours et Exercices
Formation d"Ing
´enieurs en Partenariat - 1`ereann´ee
´Ecole Nationale Sup´erieure de Physique de StrasbourgUniversit
´e de Strasbourg
Edouard Laroche (laroche@unistra.fr)
Houssem Halalchi (Houssem.Halalchi@lsiit.u-strasbg.fr) http://eavr.u-strasbg.fr/ ~laroche/student2009-2010
Table des mati`eres1 Introduction7
1.1 Notion de syst`eme . . . . . . . . . . . . . . . . . . . . . . . . 7
1.2 Propri´et´es des syst`emes . . . . . . . . . . . . . . . . . . . . . . 7
1.3 Syst`emes ´el´ementaires . . . . . . . . . . . . . . . . . . . . . . 8
1.3.1 Syst`eme du premier ordre . . . . . . . . . . . . . . . . 8
1.3.2 Syst`eme du deuxi`eme ordre . . . . . . . . . . . . . . . 9
1.4 Objectif de l"asservissement . . . . . . . . . . . . . . . . . . . 12
2 Mod´elisation15
2.1 Transform´ee de Laplace, fonctions de transfert . . . . . . . .. 15
2.1.1 Transform´ee de Laplace . . . . . . . . . . . . . . . . . 15
2.1.2 Fonction de transfert . . . . . . . . . . . . . . . . . . . 17
2.2 Propri´et´es des syst`emes dynamiques . . . . . . . . . . . . . . . 20
2.2.1 Stabilit´e . . . . . . . . . . . . . . . . . . . . . . . . . . 20
2.2.2 Gain . . . . . . . . . . . . . . . . . . . . . . . . . . . . 23
2.2.3 D´epassement . . . . . . . . . . . . . . . . . . . . . . . 23
2.2.4 Rapidit´e . . . . . . . . . . . . . . . . . . . . . . . . . . 24
2.3 Analyse fr´equentielle . . . . . . . . . . . . . . . . . . . . . . . 27
2.3.1 R´egime harmonique . . . . . . . . . . . . . . . . . . . . 27
2.3.2 Diagramme de Nyquist . . . . . . . . . . . . . . . . . . 28
2.3.3 Diagramme de Bode . . . . . . . . . . . . . . . . . . . 28
2.3.4 Diagramme de Black-Nichols . . . . . . . . . . . . . . . 31
2.3.5´Etude du second ordre . . . . . . . . . . . . . . . . . . 31
2.4 Repr´esentation d"´etat . . . . . . . . . . . . . . . . . . . . . . . 33
2.4.1 Introduction . . . . . . . . . . . . . . . . . . . . . . . . 33
2.4.2´Equivalence avec la fonction de transfert . . . . . . . . 34
2.4.3 Propri´et´es . . . . . . . . . . . . . . . . . . . . . . . . . 34
2.5 Identification . . . . . . . . . . . . . . . . . . . . . . . . . . . 36
34TABLE DES MATI`ERES
2.5.1 Approche temporelle . . . . . . . . . . . . . . . . . . . 36
2.5.2 Approche fr´equentielle . . . . . . . . . . . . . . . . . . 39
3 Asservissements analogiques 43
3.1 Introduction aux asservissements . . . . . . . . . . . . . . . . 43
3.1.1 Principe . . . . . . . . . . . . . . . . . . . . . . . . . . 43
3.1.2 Boucle ouverte ou boucle ferm´ee? . . . . . . . . . . . . 44
3.1.3 Principes g´en´eraux sur la synth`ese de correcteurs en
boucle ferm´ee (feedback) . . . . . . . . . . . . . . . . . 453.1.4 Lieu d"Evans . . . . . . . . . . . . . . . . . . . . . . . 47
3.1.5 Exemple introductif . . . . . . . . . . . . . . . . . . . . 48
3.2 Analyse des syst`emes asservis . . . . . . . . . . . . . . . . . . 57
3.2.1 Stabilit´e . . . . . . . . . . . . . . . . . . . . . . . . . . 57
3.2.2 Rapidit´e . . . . . . . . . . . . . . . . . . . . . . . . . . 58
3.2.3 Pr´ecision . . . . . . . . . . . . . . . . . . . . . . . . . . 58
3.2.4 D´epassement . . . . . . . . . . . . . . . . . . . . . . . 58
3.2.5 Rejet de perturbation . . . . . . . . . . . . . . . . . . . 59
3.3 M´ethodes de synth`ese . . . . . . . . . . . . . . . . . . . . . . . 60
3.3.1 Les diff´erentes d´emarches . . . . . . . . . . . . . . . . . 60
3.3.2 Correcteur proportionnel (P) . . . . . . . . . . . . . . . 60
3.3.3 Correcteur proportionnel int´egral (PI) . . . . . . . . . 61
3.3.4 Correcteur proportionnel d´eriv´e (PD) . . . . . . . . . . 65
3.3.5 Correcteur PID . . . . . . . . . . . . . . . . . . . . . . 66
3.3.6 Correcteur `a avance de phase . . . . . . . . . . . . . . 66
3.3.7 Correcteur `a retard de phase . . . . . . . . . . . . . . . 67
A D´ecomposition en ´el´ements simples 69Liste des exercices
1 Transform´ee de Laplace . . . . . . . . . . . . . . . . . . . . . . . 18
2 Fonctions de transfert d"un moteur `a courant continu . . . . .. . 20
3 Crit`ere de Routh-Hurwitz . . . . . . . . . . . . . . . . . . . . . . 22
4 D´epassement d"un syst`eme du second ordre . . . . . . . . . . . . 24
5 Temps d"´etablissement de syst`emes du premier ordre . . . . . . . 26
6 Diagramme de Bode d"un syst`eme du premier ordre . . . . . . . . 29
7 Trac´e du diagramme de Bode . . . . . . . . . . . . . . . . . . . . 31
8 Gain du second ordre `a la r´esonance . . . . . . . . . . . . . . . . 33
TABLE DES MATI`ERES5
9 Fonction de transfert d"un syst`eme d"´etat . . . . . . . . . . . . . . 34
10 Mod`ele d"un moteur `a courant continu . . . . . . . . . . . . . . . 35
11 Syst`eme masses-ressort . . . . . . . . . . . . . . . . . . . . . . . . 35
12 Identification d"un syst`eme du second ordre amorti . . . . . . . .39
13 Identification d"un syst`eme du second ordre oscillant . . . . . .. 39
14 Identification fr´equentielle d"un syst`eme du premier ordre . . . . . 41
15 Identification fr´equentielle d"un syst`eme du second ordre. . . . . 41
16 Correcteur TOR `a hyst´er´esis . . . . . . . . . . . . . . . . . . . . . 46
17 Variateur de vitesse . . . . . . . . . . . . . . . . . . . . . . . . . . 49
18 Marge de phase et d´epassement . . . . . . . . . . . . . . . . . . . 59
19 Correction prop. d"un syst`eme du premier ordre . . . . . . . . . .60
20 Correcteur prop. d"un syst`eme du second ordre . . . . . . . . . . 61
21 Correcteur PI pour syst`eme du premier ordre . . . . . . . . . . . 62
22 Asservissement PI d"un syst`eme du second ordre . . . . . . . . . . 62
23 Correction PI d"un syst`eme `a retard . . . . . . . . . . . . . . . . 63
24 Correcteur PD et syst`eme du second ordre . . . . . . . . . . . . . 65
25 Correction `a avance de phase pour int´egrateur double . . .. . . . 66
26 D´ecomposition en ´el´ements simples . . . . . . . . . . . . . . . . . 70
6TABLE DES MATI`ERES
"C"est le rˆole essentiel du professeur d"´eveiller la joiede travailler et de connaˆıtre." (Albert Einstein)Chapitre 1Introduction1.1 Notion de syst`eme
Consid´erons un syst`eme sur lequel on mesure le signaly(t) appel´esignal de mesureet sur lequel on peut fixer arbitrairement le signalu(t) appel´e signal de commande. Dans le cas pr´esent, les signaux sont `atemps con- tinu. Il existe ´egalement des syst`emes `a temps discret faisant intervenir les signaux ´echantillonn´esuk=u(kTe) etyk=y(kTe) o`uTeest la p´eriode d"´echantillonage. Les syst`emes `a temps continu sont mod´elis´es par une´equation diff´erentielle liantu(t) ety(t) alors que les syst`emes `a temps discret sont mod´elises par une ´equation aux r´ecurrences de la formeyk=f(yk-1,yk-2,···,uk,uk-1,···).1.2 Propri´et´es des syst`emes
Consid´erons dans un premier temps que l"entr´eeu(t) est constante.D´efinition (Point d"´equilibre)
Le syst`eme est dans un ´etat d"´equilibre si, plac´e dans cet´etat, il ne quitte pas. La valeur du signal de mesure est alors constante.D´efinition (Stabilit´e)
Un ´etat d"´equilibre est stable si, lorsqu"on ´eloigne le syst`eme de cet ´etat, il finit par y revenir. Dans le cas contraire, le point d"´equilibre est instable. 78CHAPITRE 1. INTRODUCTION
Dans certain cas, cette propri´et´e de stabilit´e n"est valable que si l"´eloigne- ment est faible; on parle alors destabilit´e locale. Si au contraire le syst`eme retourne dans son ´etat d"´equilibre quelque soit l"amplitude de la perturbation, on parle alors destabilit´e globale.Propri´et´e (Stabilit´e d"un syst`eme)
Un ´equilibre globalement stable est unique. On dit alors quele syst`eme est stable. Si le syst`eme avait deux´equilibres globaux, vers lequel irait il si on le d´epla¸cait de l"un des points d"´equilibre?Propri´et´e (Lin´earit´e)
Un syst`eme est lin´eaire s"il v´erifie les conditions de lin´earit´e suivantes. Soit y1(t)la trajectoire de la sortie pour une commandeu1(t); soity2(t)la tra-
jectoire de la sortie pour une commandeu2(t); soity3(t)la trajectoire de la sortie pour une commandeu3(t) =λu1(t)et soity4(t)la trajectoire de la sortie pour une commandeu4(t) =u1(t) +u(2). Les conditions de lin´earit´e sont : y3(t) =λy1(t) (1.1)
y4(t) =y1(t) +y2(t) (1.2)
1.3 Syst`emes ´el´ementaires
1.3.1 Syst`eme du premier ordre
Soit un syst`eme du premier ordre r´egit par une ´equation diff´erentielle de la formeτy(t) +y(t) =Ku(t) (1.3)
La r´eponse `a un ´echelonu(t) `a partir d"une condition initiale nulle est : y(t) =K(1-exp(-t/τ)) (1.4) Il s"agit d"une exponentielle partant de 0 `at= 0 et se stabilisant `ay(t) =K. Son d´epassement est nul; le temps de mont´e `a 5 % est ´egal `a 3τ(ln(0.05)≂= -3,0).1.3. SYST`EMES´EL´EMENTAIRES9
1.3.2 Syst`eme du deuxi`eme ordre
Soit un syst`eme du deuxi`eme ordre r´egit par une ´equation diff´erentielle de la forme : ¨y(t) + 2ξω0y(t) +ω20y(t) =ω20Ku(t) (1.5) o`uω0(rad/s) est appel´ee pulsation propre,ξ(sans unit´e) est appel´e amor- tissement etK(unit´es [y]/[u] d´ependant des unit´es deuet dey) est le gain statique. L"´equation associ´ee s"´ecrit : r2+ 2ξω0r+ω02= 0 (1.6)
Le discriminent r´eduit s"´ecrit :
Δ = (ξω0)2-ω02= (ξ2-1)ω02(1.7)
Les racines de (??) sont alors r´eelles si˜Δ≥0, c"est-`a-dire siξ≥1; elles sont
imaginaires dans le cas contraire.Deuxi`eme ordre amorti
Dans le cas o`u les racines sont r´eelles et s"´ecrivent : r1=-ξω0+?
ξ2-1ω0,(1.8)
r2=-ξω0-?
ξ2-1ω0,(1.9)
la solution g´en´erale de l"´equation sans second membre s"´ecrit alors : y1(t) =λexp(r1t) +μexp(r2t) (1.10)
Notons quer1etr2sont toutes deux n´egatives; l"exponentielle tend donc vers z´ero. Une solution particuli`ere constante de l"´equation sans secondmembre peut ˆetre facilement trouv´ee : y0(t) =K(1.11)
En additionnant la solution particuli`ere et l"´equation g´en´erale de l"´equation sans second membre, on obtient la solution g´en´erale de l"´equation compl`ete : y(t) =λexp(r1t) +μexp(r2t) +K(1.12)10CHAPITRE 1. INTRODUCTION
Cherchons maintenant la solution v´erifiant les conditions initiales suivantes : y(0) = 0 (1.13) y(0) = 0 (1.14)La d´eriv´ee de la solution s"´ecrit :
y(t) =λr1exp(r1t) +μr2exp(r2t) (1.15)Les C.I. s"´ecrivent alors :
λ+μ+K= 0 (1.16)
λr1+μr2= 0 (1.17)
Dont les solutions sont :
λ=Kr2
r1-r2(1.18)μ=-Kr1
r1-r2(1.19)La solution s"´ecrit alors :
y(t) =K(1 +r2 r1-r2exp(r1t)-r1r1-r2exp(r2t)) (1.20)Sa d´eriv´ee est :
y(t) =Kr1r2 r1-r2(exp(r1t)-exp(r2t)) (1.21) et y(t) est alors positive pourt≥0, ce qui signifie quey(t) est croissante. La r´eponse `a un ´echelon est donc une courbe croissante qui se stabilise `a la valeurK. Cette courbe a un point d"inflexion pour ¨y(ti) = 0. Avec :¨y(t) =Kr1r2
r1-r2(r1exp(r1t)-r2exp(r2t)),(1.22) on observe que la d´eriv´ee seconde n"annule entiv´erifiant : r1exp(r1t)-r2exp(r2t),(1.23)
soit t i=1 r1-r2lnr2r1.(1.24)1.3. SYST`EMES´EL´EMENTAIRES11
Deuxi`eme ordre oscillant
Dans le cas o`u les racines sont complexes conjug´ees et s"´ecrivent : r1=-a+jω1,(1.25)
r2=-a-jω1,(1.26)
avec a=ξω0(1.27) 1=?1-ξ2ω0,(1.28)
o`uω1est la pseudo-pulsation de la r´eponse, li´ee `a la p´eriode des oscillations T c=2π ω1. La solution g´en´erale de l"´equation sans second membre s"´ecrit alors : y1(t) = exp(-at)(λcos(ω1t) +μsin(ω1t)) (1.29)
Notons queaest positif; l"exponentielle tend donc vers z´ero. Une solution particuli`ere constante s"´ecrity0(t) =K. La solution g´en´erale de l"´equation est donc : y(t) =K+ exp(-at)(λcos(ω1t) +μsin(ω1t)) (1.30) Reste `a d´eterminer les constantesλetμd"apr`es les conditions initiales (1.13-1.14). On a :
y(t) =-aexp(-at)(λcos(ω1t) +μsin(ω1t)) (1.31) +ω1exp(-at)(-λsin(ω1t) +μcos(ω1t)) (1.32) = exp(-at)((-aλ+ω1μ)cos(ω1t)-(ω1λ+aμ)sin(ω1t))(1.33)Les conditions initiales s"´ecrivent alors :
y(0) =K+λ= 0 y(0) =-aλ+ω1μ= 0(1.34) ce qui donne :λ=-K(1.35)
μ=-Ka
ω1(1.36)
12CHAPITRE 1. INTRODUCTION
ce qui donne comme solution finale : y(t) =K?1-exp(-at)?
cos(ω1t) +aω1sin(ω1t)??
(1.37)La vitesse s"´ecrit alors :
y(t) =Ka2+ω21ω1exp(-at)sin(ω1t) (1.38)
Elle est du signe du terme sin(ω1t). Elle est d"abord positive det= 0 `a t1=π
ω1puis n´egative det1`a2πω1. Le signal atteint donc un maximum `at1en : y(t1) =K?1 + exp?
?1-ξ2?? (1.39) soit un d´epassement relatif (y(t1)-y(∞))/(y(∞)-y(0)) de :D= exp?
?1-ξ2? (1.40)1.4 Objectif de l"asservissement
Un syst`eme dynamique peut ˆetre caract´eris´e par diff´erentes qualit´es : sa rapidit´e, le fait d"ˆetre plus ou moins amorti. Le but de l"asservissement est de contraindre le syst`eme `a se comporter d"une mani`ere particuli`ere. Il n"est pas possible physiquement d"obtenir d"un syst`eme qu"il r´eponde de mani`ere instantan´ee. On peut cependant le contraindre `a r´epondreplus rapidement.On peut aussi limiter son d´epassement.
Dans le choix de laloi de commande, il faudra ´egalement s"assurer que le syst`eme asservi poss`ede un niveau derobustessesuffisant. Par robustesse, on entend la capacit´e `a garder certaines propri´et´es malgr´e des variation de l"environnement. Typiquement, en automatique, le comportement du syst`eme est connu avec une pr´ecision limit´ee; de plus, son comportemetpeu ´evoluer en fonction de condition ext´erieure ou de son vieillissement.Il importe que les performances du syst`eme asservi ne se d´egrade pas trop en pr´esence de ces variations de comportement.1.4. OBJECTIF DE L"ASSERVISSEMENT13
0510150
0.5 1 1.5 Réponse à un échelon unitaire de 1/(p2+2 ξ p+1)Temps (s)
Fig.1.1 - R´eponse temporelle de syst`emes du second ordre (ξ= 0.25, 0.5,0.707, 1 et 2)
14CHAPITRE 1. INTRODUCTION
Chapitre 2Mod´elisation
Dans cette partie, on s"int´eresse `a la d´etermination de mod`eles math´ema- tique pour des syst`emes lin´eaires stationaires (on parle ausside syst`emes lin´eaire `a temps invariant, not´es LTI en anglais). Les mod`eles peuvent ˆetre abord´es sous trois formes `a peu pr`es ´equivalentes : l"´equation diff´erentielle, la fonction de transfert et le mod`ele d"´etat.2.1 Transform´ee de Laplace, fonctions de trans-
fert2.1.1 Transform´ee de Laplace
D´efinition
Pour un signal `a temps continux(t), on d´efinit sa transform´ee de Laplace par le signalX(s) o`usest appel´ee variable de Laplace1, avec :X(s) =?
0 x(t)exp(-st)dt(2.1) A partir deX(s), on revient au signal de d´epart par une transform´ee deLaplace inverse :
x(t) =12jπ?
j∞ s=-j∞X(s)exp(st)ds(2.2)1La variable de Laplace est not´essoupsuivant les conventions.
1516CHAPITRE 2. MOD´ELISATION
h(t) H(s)δ(t)1
u(t) 1 s u(t-T) exp(-Ts) s tu(t) 1 s2 t n n!u(t) 1 sn+1 exp(-at)u(t) 1 s+a (1-exp(-at))u(t) a s(s+a) sin(ωt)u(t) s2+ω2 cos(ωt)u(t) s s2+ω2 sinh(at)u(t) a s2-a2 cosh(at)u(t) s s2-a2 exp(-at)sin(ωt)u(t) (s+a)2+ω2 exp(-at)cos(ωt)u(t) s+a (s+a)2+ω2quotesdbs_dbs22.pdfusesText_28[PDF] exercice corrigé méthode des centres d'analyse
[PDF] exercice corrigé methode des couts complets
[PDF] exercice corrigé méthode des couts variables
[PDF] exercice corrigé méthode des moindres carrés
[PDF] exercice corrigé méthode des moments
[PDF] exercice corrigé méthode des trapèzes
[PDF] exercice corrigé modele wilson
[PDF] exercice corrigé moment d'une force
[PDF] exercice corrigé moteur à courant continu à excitation indépendante
[PDF] exercice corrigé moteur à excitation indépendante
[PDF] exercice corrigé moteur courant continu
[PDF] exercice corrigé moteur de stirling
[PDF] exercice corrigé moteur pas a pas
[PDF] exercice corrigé mouvement d'un systeme 1ere
