 Exercices de géométrie - Isométries et Homothéties (IH)
Exercices de géométrie - Isométries et Homothéties (IH)
Exercices de géométrie - Isométries et Homothéties (IH). Copyright (c) 2008 - Gabriele Mondada - www.ecoleaquarelle.ch. Permission vous est donnée de copier
 EPFL
EPFL
29 avr. 2020 Tous les exercices sont `a faire sur des feuilles `a part. Garde la donnée pour ... (3) Peut-on énoncer un nouveau cas d'isométrie des triangles?
 LES CAS DISOMETRIE ET LES AIRES DES OUTILS DE
LES CAS DISOMETRIE ET LES AIRES DES OUTILS DE
8 juin 2022 De plus dans toutes les preuves par les transformations de cet exercice
 QUAND LE MANUEL UNIQUE DEVIENT LA RESSOURCE
QUAND LE MANUEL UNIQUE DEVIENT LA RESSOURCE
d'isométrie). -. La disponibilité des isométries comme outil pour résoudre les exercices et les problèmes qui peuvent êtres traités à ce niveau. Cette
 Stabilisateurs groupes disométries et représentations
Stabilisateurs groupes disométries et représentations
On notera A B
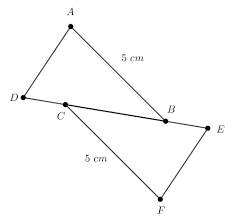 Cas disométries des triangles
Cas disométries des triangles
(2) repérer si deux triangles sont isométriques en vérifiant si trois éléments homologues sont isométriques. 5.12. Page 13. 3. Exercices. 3.1. Connaître.
 1.60 - 644 265 - 02-2023 - Tendinopathie patellaire.docx
1.60 - 644 265 - 02-2023 - Tendinopathie patellaire.docx
Construire un programme d'exercices progressifs visant à redonner les capacités de charge du tendon. Ce programme consiste à partir de l'isométrique pour
 Triangles isométriques
Triangles isométriques
Triangles isométriques. 6. Exercices sur les cas d'isométrie. Pour chacune des paires de triangles suivantes indique si ces triangles sont isométriques et avec
 EPFL
EPFL
8 janv. 2020 Exercice 2. Relis attentivement la preuve de la proposition du cours qui affirme qu'une isométrie est une rotation.
 EPFL
EPFL
16 janv. 2019 Exercice 2. Relis attentivement la preuve de la proposition du cours qui affirme qu'une isométrie est une rotation.
 EXERCICES SUR LES ISOMÉTRIES ET SIMILITUDES Exercice 1
EXERCICES SUR LES ISOMÉTRIES ET SIMILITUDES Exercice 1
Exercices Isométries Similitudes Page 1 sur 5 Adama Traoré Professeur Lycée 1°) Montrer que f est une isométrie affine. f est-e lle un déplacement ? un.
 Exercices de révision sur les isométries :Correctif - ddm-vergote
Exercices de révision sur les isométries :Correctif - ddm-vergote
Exercices de révision sur les isométries :Correctif. Théorie : Dans certains exercices tu verras que l'on parle d'angles alternes-internes ou alternes.
 Stabilisateurs groupes disométries et représentations
Stabilisateurs groupes disométries et représentations
groupe des isométries (resp. isométries directes) de E. Exercice 1 (Stabilisateur d'une partie convexe). Soit C un convexe compact d'intérieur non.
 Triangles isométriques
Triangles isométriques
Des triangles isométriques sont. Chapitre 4 Voici le récit entre un élève et son maitre parlant des cas d'isométries ... Résous les exercices suivants ...
 Cas disométries des triangles
Cas disométries des triangles
Certains énoncés qui figurent dans les exercices peuvent être démontrés de plusieurs façons notamment par les invariants des isométries ; mais
 Feuille dexercices no 6
Feuille dexercices no 6
donc une isométrie directe c'est-à-dire une rotation. D'après l'exercice précédent on peut décomposer toute rotation plane d'angle ? en le produit de ...
 ISOMÉTRIES DU PLAN AFFINE EUCLIDIEN Voici un cours sur les
ISOMÉTRIES DU PLAN AFFINE EUCLIDIEN Voici un cours sur les
Exercices. 15. 4. Droites invariantes par des isométries. 15. 4.1. Translation. 15. 4.2. Symétrie centrale. 15. 4.3. Réflexion. 16. 4.4. Symétrie glissée.
 FR_?wiczenia izometryczne
FR_?wiczenia izometryczne
Exercices isométriques universels pour tous quelque soit la condition physique actuelle. Bien que la notion d'isométrie vient des mathématiques (géométrie)
 LES ISOMÉTRIES DU PLAN
LES ISOMÉTRIES DU PLAN
Exemples : la translation la symétrie orthogonale sont des isométries. c) Déplacements et antidéplacement : Exercice d'application :.
 Exercices de géométrie - Isométries et Homothéties (IH)
Exercices de géométrie - Isométries et Homothéties (IH)
Textes des exercices. Exercice GMO-IH-1. Mots-clés: 7S translation
Année 2020-2021
Feuille d"exercices n
o6Exercice 1
Déterminer la composée de deux symétries vectorielles orthogonales planes.Déterminer l"ordre de cette composée.
Solution 1
Le déterminant d"une symétrie orthogonale est-1; la composéer=s?sde deux telles symétriessets?est
donc une isométrie directe, c"est-à-dire une rotation.Déterminons l"angleθde la rotation à partir des axes respectifsR-→uetR-→u?(-→uet-→u?unitaires) des symétries
sets?. Pour cela il suffit de déterminer l"image de-→uparr, ou plutôt l"angle(-→u ,r(-→u)). Puisques(-→u) =-→u
nous avonsr(-→u) =s?(-→u)donc l"angle(-→u ,r(-→u))est aussi l"angle(-→u ,s?(-→u)). Comme une symétrie renverse
l"orientation nous avons (-→u ,-→u?) =-(s?(-→u),s?(-→u?)) d"où (-→u ,-→u?) = (s?(-→u?),s?(-→u)).Puisque
-→u?appartient à l"axe des?nous obtenons -→u ,-→u?) = (-→u?,s?(-→u)).Il en résulte que
θ= (-→u ,s?(-→u)) = (-→u ,-→u?) + (-→u?,s?(-→u)) = 2(-→u ,-→u?)
Notons que
-→upeut être remplacé par--→uou-→u?par--→u?. L"angle(-→u ,-→u?)n"est donc défini qu"àπprès à
partir de la donnée des deux symétries (ce n"est pas étonnant : la seule donnée intrinsèque est l"angle de droites
(R-→u ,R-→u?)). Mais grâce à la multiplication par2l"angleθse trouve être bien défini à2πprès.
Déterminons l"ordre de cette composée. L"ordre d"une rotation est infini si l"angle de la rotation n"est pas
égal à
2kπn
pournetkentiers. L"ordre de la rotation d"angle2kπn pournetkpremiers entre eux estn.Exercice 2
Montrer que toute rotation plane se décompose en le produit de deux symétries. Que pouvons-nous dire pour les rotations de l"espace?Solution 2
Montrons que toute rotation plane se décompose en le produit de deux symétries.D"après l"exercice précédent on peut décomposer toute rotation plane d"angleθen le produit de deux
symétries orthogonales : l"axe de la première est choisi au hasard, l"axe de la seconde fait un angle de
θ2 avec la première.Il y a un résultat analogue pour une rotation de l"espace d"axeRuet d"angleθ. Elle se décompose en le
produit de deux symétries orthogonales par rapport à deux plans vectoriels contenantRuet qui font un angle
égal à
θ2 entre eux : la restriction de la rotation au plan vectoriel orthogonal àRuest une rotation plane.Exercice 3[Le groupe diédral]
Considérons un polygone régulier ayant un sommetPde coordonnées(1,0)et centré à l"origine du repère.
1. Déterminer le groupeD6des isométries du plan qui conservent un triangle équilatéral. Établir la table de
D 6. 12. Déterminer le groupeD8des isométries du plan qui conservent un carré. Déterminer les ordres des éléments
deD8. Établir la table deD8.3. Déterminer le groupeD2ndes isométries du plan qui conservent un polygone régulier àncôtés.
Solution 3
NotonsOl"origine deR2. MunissonsR2de l"orientation géométrique.1. Commençons par déterminer les isométries (i.e.les symétries axiales et les rotations centrées enO) qui
fixent un des sommets du triangle équilatéral. En dehors de l"identité il y a la symétrie d"axe la médiane
issue du sommet considéré. Comme il y a trois sommets on obtient ainsi trois symétries dansD6.
Par ailleurs il y a les deux rotations centrées enOd"angle2π3 et4π3En ajoutant l"identité cela fait déjà6éléments dansD6. Or une isométrie affine qui conserve le triangle
équilatéral induit une permutation sur l"ensemble des sommets du triangle équilatéral qui sont au nombre
de trois. Par suiteD6est un sous-groupe deS3.Il y a3! = 6permutations de ces trois sommets doncD6? S3et nous avons listé tous les éléments deD6.
Désignons parA1,A2etA3les sommets du triangle équilatéral. Pour16i63notonssila symétrie qui
laisse le pointAifixe,r1la rotation d"angle2π3 etr22=r1la rotation d"angle4π3La table deD6? S3est la suivanteids
1s 2s 3r 1r2idids
1s 2s 3r 1r 2s 1s 1idr 1r 2s 2s 3s 2s 2r 2idr 1s 3s 1s 3s 3r 1r 2ids 1s 2r 1r 1s 3s 1s 2r 2id r 2r 2s 2s 3s 1idr12. Notons qu"une isométrie qui préserve un carré envoie chaque sommet sur un sommet, chaque côté sur un
côté et chaque diagonale sur une diagonale.Déterminons les isométries du plan qui conservent le carré[A1,A2,A3,A4]et qui laissent fixe le pointA1.
De telles isométries laissent donc fixe la diagonale[A1,A3]et donc le pointA3. Il n"y en a donc qu"une
non triviale : la symétrie par rapport à cette diagonale.Cherchons les isométries du plan qui conservent le carré[A1,A2,A3,A4]et qui envoient le pointA1sur le
pointA2. De telles isométries envoient donc la diagonale[A1,A3]sur la diagonale[A2,A4]. Il en résulte
queA3a pour imageA4. Il y a deux telles isométries ?la symétrie par rapport à la médiatrice commune de[A1,A2]et[A3,A4]qui envoieA4surA3etA2 surA1; ?la rotation d"angle3π2 qui envoieA4surA1etA2surA3.Cherchons les isométries du plan qui conservent le carré[A1,A2,A3,A4]et qui envoient le pointA1sur le
pointA4. De telles isométries envoient donc la diagonale[A1,A3]sur la diagonale[A2,A4]; le pointA3a
donc pour image le pointA2. Il y en a donc deux : ?la symétrie par rapport à la médiatrice commune de[A1,A4]et[A2,A3]qui envoieA4surA1etA2 surA3; ?la rotation d"angleπ2 qui envoieA4surA3etA2surA1. Restent les isométries qui envoientA1surA3en conservant le carré. La diagonale[A2,A4]est alors préservée. Il y en a deux : ?la symétrie par rapport à la diagonale[A2,A4]; ?la rotation d"angleπ.Notations :
?r1la rotation d"angleπ2 ?r2la rotation d"angleπ; ?r3la rotation d"angle3π2 ?s12la symétrie d"axe la médiatrice de[A1,A2]; ?s23la symétrie d"axe la médiatrice de[A2,A3]; ?s13la symétrie d"axe la médiatrice de[A1,A3]; ?s24la symétrie d"axe la médiatrice de[A2,A4]. Chacune des symétries est d"ordre2;r1etr3sont d"ordre4etr2est d"ordre2.La table deD8est
2 idr 1r 2r 3s 12s 23s13s
24ididr
1r 2r 3s 12s 23s13s 24r
1r 1r 2r 3ids 13s 24s
23s
12r 2r 2r 3idr 1s 23s
12s 24s
13r 3r 3idr 1r 2s 24s
13s 12s 23s
12s 12s 24s
23s
13idr 2r 3r 1s 23s
23s
13s 12s 24r
2idr 1r 3s 13s 13s 12s 24s
23r
1r 3idr 2s 24s
24s
23s
13s 12r 3r 1r 2id
3. SoitPun polygone régulier àncôtés. Numérotons les sommets dePndans le sens trigonométrique, il
s"écrit[A1,A2,...,An].Pour une isométrie conservant le polygone chaque sommet va sur un sommet, chaque côté va sur un côté
donc siA1a pour imageAkalorsA2a pour image soitAk-1soitAk+1. Dans le premier cas l"isométrieest une symétrie (car ce n"est pas un élément deSO(2,R)), dans le second cas l"isométrie est une rotation
d"angle2kπn
. Les axes de symétrie possibles sont ?sinest pair les droites déterminées par un sommet quelconque et le centre (il y en an2 ) et les droites déterminées par les médiatrices des côté (il y en a n2?sinest impair, les droites déterminées par un sommet quelconque et le centre qui sont les droites
déterminées par les médiatrices des côtés (il y en an).Soitrla rotation d"angle2πn
et soitsl"une des symétries deD2n. Le groupeD2nest engendré parsetr.Exercice 4
Déterminer le groupe des isométries du plan qui conservent un rectangle non carré.Établir la table de ce groupe.
Solution 4
Considérons un rectangleABCDtel que "Aest le coin en haut à gauche,Ble coin en haut à droite,Cle
coin en bas à droite,Dle coin en bas à gauche,[AB]et[CD]sont les longueurs et[BC]et[AD]les largeurs."
Prenons pour origine du repère le centre du rectangle.Une isométrie qui conserve le rectangle laisse fixe le centre du rectangle donc le groupe recherché est iso-
morphe à un sous-groupe du groupe des isométries vectorielles. Par ailleurs une isométrie qui conserve le rec-
tangle envoie chaque diagonale sur une diagonale.Une isométrie qui conserve le rectangle et laisse fixe le sommetAlaisse fixe la diagonale[AC]et donc le
sommetCet tous les autres sommets. Ainsi la seule isométrie qui conserve le rectangle et laisse fixe le sommet
Aest l"identité. Il en est de même lorsque l"on remplaceAparB(resp.C, resp.D). Une isométrie qui conserve
le rectangle et qui n"est pas l"identité ne fixe donc aucun sommet.?ou bienAa pour imageBalorsCa pour imageDet cette isométrie est la symétries1d"axe la médiatrice
de[AB];?ou bienAa pour imageD, alorsBa pour imageCet cette isométrie est la symétries2d"axe la médiatrice
de[AD]; ?ou bienAetCsont échangés et cette isométrie est la rotationrd"angleπ. On a donc un groupe d"ordre4, abélien, dont la table est :ids 1s 2r idids 1s 2r s 1s 1idrs 2s 2s 2rids 1rrs 2s 1idExercice 5
Soitn>3; le sous-ensemble?g?D2n|g2= id?deD2nest-il un sous-groupe deD2n?Solution 5
La composée de deux symétries orthogonales éléments deD2nest une rotation d"angle deux fois l"angle
formé par les deux axes. Par suite dès quen>3l"un de ces produits au moins est d"ordre différent de2. Ainsi
l"ensemble des éléments d"ordre2deD2nn"est pas un sous-groupe deD2n.Exercice 6
3 Quelle est la matrice de la rotation deR3d"angleθautour de l"axeRe2?Solution 6
Le vecteure2est vecteur propre pour la valeur propre1de la matrice,i.e.c"est un vecteur fixe pour la rotation considérée. L"image dee1est dans le plan(e1,e3)et est égale àcosθe1-sinθe3. L"image dee3est dans le plan(e1,e3)et est égale àsinθe1+ cosθe3.La matrice cherchée est donc
(cosθ0 sinθ 0 1 0 -sinθ0 cosθ)Exercice 7
SoitM?O(3,R)de déterminant-1.
Montrer que-1est valeur propre deM.
Solution 7
Puisque une isométrie vectorielle conserve les normes, ses valeurs propres sont de module1. Ceci est donc
vrai pour une matriceMdeO(3,R)qui est la matrice d"une isométrie vectorielle. Si de plusdetM=-1, alors
le produit des racines du polynôme caractéristique deMest-1. Par suite•ou bien toutes les racines du polynôme caractéristique deMsont réelles et dans ce cas l"une ou trois
d"entre elles sont égales à-1;•ou bien deux d"entre elles sont complexes conjuguées, leur produit étant égal à1la dernière est-1.
Exercice 8
SoitMune matrice orthogonale2×2et de déterminant-1. Montrer queMest la matrice d"une symétrie orthogonale.Solution 8
Les racines du polynôme caractéristique deMsont de module1. Si elles sont complexes conjuguées mais
dans ce cas le déterminant deMest1: contradiction. Elles sont donc toutes les deux réelles, l"une valant1et
l"autre-1.Il s"en suit queMest la matrice de la symétrie orthogonale d"axe la droite vectorielle propre associée à la
valeur propre1.Exercice 9
SoitM?SO(3,R)la rotation d"angleθ. Montrer que
cosθ=12TrM-1?
Solution 9
SiMest la matrice d"une rotation d"angleθ, alorsMest semblable à la matrice (cosθ-sinθ0 sinθcosθ00 0 1)
Par suiteTrM= 2cosθ+ 1etcosθ=12
TrM-1?
Exercice 10
Soitsune symétrie plane d"axeD.
1. Soittune translation de vecteur-→v. Montrer que la composéet◦s(resp.s◦t) est une symétrie si et
seulement si-→vest normal àD.2. Soitrune rotation de centreC. Montrer que la composéer◦s(resp.s◦r) est une symétrie si et seulement
siCappartient àD. 43. Soients?ets??deux symétries axiales. Montrer ques◦s?◦s??est une symétrie si et seulement si les axes
des?ets??sont parallèles àDou se rencontrent en un point deD.Solution 10
1. Soittune translation de vecteur-→v. Montrons que la composéet◦s(resp.s◦t) est une symétrie si et
seulement si-→vest normal àD.Supposons-→vnormal àD. Soitt?(D?) =D?oùt?est la translation de vecteur-→v /2. La droiteD?est une
droite de points fixes partsqui est donc la symétrie orthogonale d"axeD?.Soitt??la translation de vecteur--→v /2. PosonsD??=t??(D). La droiteD??est une droite de points fixes
parstqui est donc la symétrie orthogonale d"axeD??. Sitsest une symétrie orthogonales?et siAest un point de l"axe de symétrie, nous avonsts(A) =Adonc----→s(A)A=-→v. Par suite-→vest normal à la droiteDet d"après ce qui précèdestest une symétrie
orthogonale. Sistest une symétrie, nous arrivons à la même conclusion.2. Soitrune rotation de centreC. Montrons que la composéer◦s(resp.s◦r) est une symétrie si et seulement
siCappartient àD.Supposons queCappartienne àD. Soitθl"angle de la rotationr. Considérons la rotationr?de centreC
et d"angle-θ2 . AlorsD?=r?(D)est une droite de points fixes des◦rqui est une symétrie d"axeD?.Soitr??la rotation de centreCet d"angleθ2
. AlorsD??=r??(D)est une droite de points fixes der◦squi est une symétrie d"axeD??.Réciproquement supposons quer◦ssoit une symétrie orthogonale d"axeD?. SoitC?l"intersection deD
etD?. Nous avonsrs(C?) =C?ainsi ques(C?) =C?. Par conséquentC?=r(C?)etC?est le centre de larotationr, c"est-à-direCqui est donc surD. Dans ce cass◦rest aussi une symétrie orthogonale.
La conclusion est identique en supposant a priori ques◦rest une symétrie.3. Soients?ets??deux symétries axiales. Montrons ques◦s?◦s??est une symétrie si et seulement si les axes
des?ets??sont parallèles àDou se rencontrent en un point deD.Supposons que les axes des?ets??soient sécants en un pointC. Alorss?◦s??est une rotation de centre
Cet d"après2. ss?s??est une symétrie si et seulement siCappartient àD.Supposons que les axes des?ets??soient parallèles alorss?◦s??est une translation de vecteur orthogonal
à la direction commune et d"après1. ss?s??est une symétrie si et seulement si cette direction commune est
celle deD.Exercice 11
Montrer que pour une translationtde vecteur-→uet une symétriesd"axeDnous avonst◦s=s◦tsi et
seulement si-→uest dans la direction deD.Solution 11
Sist=ts, alors pour tout pointMdeDnous avonsst(M) =ts(M) =t(M)donct(M)appartient àDet -→u=-----→Mt(M)est parallèle àD.Réciproquement supposons que-→usoit parallèle àD. PosonsM?=ts(M)etM??=st(M). Nous avons-----→Ms(M) =---------→t(M)s(t(M)) =------→t(M)M??. Par conséquent------→s(M)M??=-----→Mt(M) =-→uet donc------→s(M)M??=---------→s(M)t(s(M)) =-----→s(M)M?M??=M?. Il s"en suit quest=ts.
Exercice 12
SoitRle réseau plan des points à coordonnées entières dans un repère orthonormal(O,-→i ,-→j).
Quelles sont les isométries affines qui conserventR? Quelles sont les centres des rotations affines qui conserventR?Solution 12
Si une isométrie affine qui conserve le réseauRa exactement un point fixe, c"est une rotation autour de
l"un des points du réseau d"angle kπ2 , ou une rotation d"anglekπ2 autour de l"un des centres des carrés du type[O,A,B,C]oùOest le centre du repère,Aa pour coordonnées(1,0),Ba pour coordonnées(1,1),Ca pour
coordonnées(0,1). Enfin il y a aussi les symétries centrales autour des milieux des segments du typeOA,AB,
BCetCO.
5Si une isométrie affine qui conserve le réseauRa une droite de points fixes, alors c"est une symétrie ortho-
gonale par rapport aux droites du typeOA,AB,BCetCO(côtés des carrés du type[O,A,B,C]) ainsi que
ACetOC(diagonales des carrés du type[O,A,B,C]) et des médiatrices des segmentsOAetAB.Si une isométrie affine qui conserve le réseauRn"a pas de point fixe, alors soit c"est une translation de
vecteur?Ze1+Ze2(où(e1,e2)est la base canonique deR2), soit c"est un produit d"une translation de ce type
avec les autres isométries affines déjà trouvées.Exercice 13
SoitSla représentation graphique dans un repère orthonormal de la fonction sinus.quotesdbs_dbs1.pdfusesText_1[PDF] exercices d'orthographe française
[PDF] exercices d'orthographe pour les nuls pdf
[PDF] exercices de bael gratuit pdf
[PDF] exercices de chimie générale - 400 exercices avec solutions - 140 qcm corrigés
[PDF] exercices de chimie organique corrigés pdf
[PDF] exercices de comptabilité générale avec corrigés détaillés pdf gratuit
[PDF] exercices de comptabilité générale bilan
[PDF] exercices de comptabilité générale ohada avec corrigés détaillés pdf gratuit
[PDF] exercices de comptabilité générale pdf
[PDF] exercices de comptabilité pour les nuls gratuit
[PDF] exercices de conjugaison ? imprimer 6ème
[PDF] exercices de conjugaison ? tous les temps ? imprimer
[PDF] exercices de conjugaison cm2 pdf
[PDF] exercices de conjugaison passé composé pdf
