 Chapitre I - Ensembles - cours et exercices
Chapitre I - Ensembles - cours et exercices
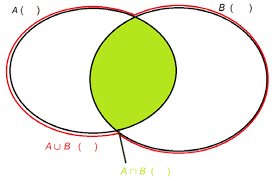
Ici les éléments intéressants sont ceux qui appartiennent à A ou à B : …………….. •. Intersection de deux ensembles inclusions possibles entre les ensembles : A ...
 1 Réunion intersection
1 Réunion intersection
produit carté- sien d'ensembles
 théorie des ensembles - une introduction
théorie des ensembles - une introduction
appartenance inclusion. 2 intersection. 3 réunion. 4 complémentaire. 5 différence symétrique. 6 exercices. 3 / 49. Page 4. Appartenance inclusion intersection.
 ensemble.pdf
ensemble.pdf
L'ensemble. {x
 1 Inclusion égalité
1 Inclusion égalité
intersection
 Chapitre 2 : ensembles
Chapitre 2 : ensembles
Inclusion ensemble des parties. On dit que l'ensemble A est inclus dans l 2 Union et intersection de deux ensembles. Dans tout ce qui suit
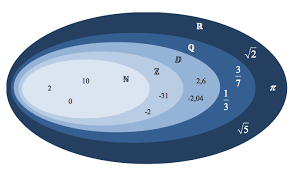 ENSEMBLES DE NOMBRES
ENSEMBLES DE NOMBRES
Intersections et unions d'intervalles : Définitions : -. L'intersection de deux ensembles A et B est l'ensemble des éléments qui Exercices conseillés En ...
 ´Enoncés des exercices
´Enoncés des exercices
Union intersection
 Corrigés des exercices Ensembles et applications
Corrigés des exercices Ensembles et applications
Pour montrer qu'une union est incluse dans un ensemble il suffit de montrer que chaque terme de l'union est inclus intersection.2 Autrement dit
 12.2 Exercices du chapitre 2 - 12.2.1 Tribus
12.2 Exercices du chapitre 2 - 12.2.1 Tribus
Si Σ est une tribu Σ est stable par union dénombrable et intersection dénombrable. L'ensemble K1 est donc compact car il est l'union de deux compacts. Comme.
 théorie des ensembles - une introduction
théorie des ensembles - une introduction
appartenance inclusion. 2 intersection. 3 réunion. 4 complémentaire. 5 différence symétrique. 6 exercices. 3 / 49. Page 4. Appartenance inclusion intersection.
 ensemble.pdf
ensemble.pdf
L'ensemble {x
 x ? A ou x ? B} est appelé lunion des ensembles A et B et est noté Exercice - Soient A B
x ? A ou x ? B} est appelé lunion des ensembles A et B et est noté Exercice - Soient A B
D des sous-ensembles d'un ensemble E.
 1 Réunion intersection
1 Réunion intersection
produit carté- sien d'ensembles
 ´Enoncés des exercices
´Enoncés des exercices
Union intersection
 Corrigés des exercices Ensembles et applications
Corrigés des exercices Ensembles et applications
Montrons que A ? B. Par définition de l'inclusion nous devons donc montrer un ensemble
 ENSEMBLES DE NOMBRES
ENSEMBLES DE NOMBRES
L'ensemble des nombres entiers naturels est noté ?. ?= 0;1;2;3;4. Exercices conseillés En devoir ... Intersections et unions d'intervalles :.
 Chapitre 2 : ensembles
Chapitre 2 : ensembles
double inclusion c'est à dire de montrer d'abord que A est inclus dans B
 1 Inclusion égalité
1 Inclusion égalité
intersection
 12.2 Exercices du chapitre 2 - 12.2.1 Tribus
12.2 Exercices du chapitre 2 - 12.2.1 Tribus
Corrigé 10 (Tribu engendrée). Soit E un ensemble. 1. Montrer qu'une intersection quelconque de tribus sur E est une tribu sur E.
 Exercices de mathématiques - Exo7
Exercices de mathématiques - Exo7
Montrer que les ensembles ci-dessous sont des espaces vectoriels (sur R) : Dans R3 donner un exemple de deux sous-espaces dont l'union n'est pas un ...
Appartenance, inclusion
intersection réunion exercices théorie des ensembles une introductionJ-P SPRIET
20131/49
Appartenance, inclusion
intersection réunion exercices Plan Voici un exposé des bases de la théorie des ensembles.1Appartenance, inclusion
2intersection
3réunion
4complémentaire
5différence symétrique
6exercices
2/49Appartenance, inclusion
intersection réunion exercices Plan1Appartenance, inclusion
appartenance inclusion2intersection
3réunion
4complémentaire
5différence symétrique
6exercices
3/49Appartenance, inclusion
intersection réunion exercicesAppartenance
SiAest un ensemble, on dit quexappartient à l'ensembleA ssixest un élément deA, et on notex?A. Dans le cas contraire on notex??A.EXEMPLE:x1??A;x2?A
A x1 x2 4/49Appartenance, inclusion
intersection réunion exercices SiAest un ensemble, on dit quexappartient à l'ensembleA ssixest un élément deA, et on notex?A. Dans le cas contraire on notex??A.EXEMPLE:
1?N;-2??Nmais-2?Z
2?Rmais⎷2??Q(démontré par les grecs)
π??Q(démontré par )
5/49Appartenance, inclusion
intersection réunion exercicesInclusion
SiAetBsont deux ensembles, on dit queAest inclus dansB, ou queAest une sous-partie deBssi tout élément deAest aussi élément deB. Et on noteA?B.EXEMPLE:A?B
BA 6/49Appartenance, inclusion
intersection réunion exercices SiAetBsont deux ensembles, on dit queAest inclus dansB, ou queAest une sous-partie deBssi tout élément deAest aussi élément deB. Et on noteA?B.EXEMPLE:
Tout entier naturel est aussi un entier relatif donc on noteN?Z Tout entier naturel est aussi un nombre réel doncN?R On a la suite d'inclusions classiques :N?Z?D?Q?R?C 7/49Appartenance, inclusion
intersection réunion exercices SiAetBsont deux ensembles, on dit queAest inclus dansB, ou queAest une sous-partie deBssi tout élément deAest aussi élément deB. Et on noteA?B. Dans le cas contraire, il existe (au moins) un élément deAqui n'appartient pas àB. Et on noteA??B, que l'on lit "An'est pas inclus dansB".EXEMPLE:A??B
BA 8/49Appartenance, inclusion
intersection réunion exercices SiAetBsont deux ensembles, on dit queAest inclus dansB, ou queAest une sous-partie deBssi tout élément deAest aussi élément deB. Et on noteA?B. Dans le cas contraire, il existe (au moins) un élément deAqui n'appartient pas àB. Et on noteA??B, que l'on lit "An'est pas inclus dansB".EXEMPLE:
Z??N: tout entier relatif n'est pas forcément un entier naturel, par exemple-1?Zmais-1??N. [0;1]??R?: par exemple 0?[0;1]mais 0??R?. 9/49Appartenance, inclusion
intersection réunion exercicesÉgalité de deux ensembles
Pour montrer queA=B, il faut et il suffit de montrer la double inclusionA?BetB?A, ce qui équivaut à montrer que tout élément deAest élément deBet réciproquement que toutélément deBest élément deA.
EXEMPLE: Montrer queA∩(B?C) = (A∩B)?(A∩C) 10/49Appartenance, inclusion
intersection réunion exercices Plan1Appartenance, inclusion
2intersection
3réunion
4complémentaire
5différence symétrique
6exercices
11/49Appartenance, inclusion
intersection réunion exercices intersection de deux ensembles On définit l'intersection de deux partiesAetBd'un ensembleE comme l'ensemble des élémentsx?Equi appartiennent à la fois àAet àB.EXEMPLE:
On considère deux disquesAetB:
A B 12/49Appartenance, inclusion
intersection réunion exercices intersection de deux ensembles On définit l'intersection de deux partiesAetBd'un ensembleE comme l'ensemble des élémentsx?Equi appartiennent à la fois àAet àB.EXEMPLE:
On considère deux disquesAetB:
A B A B en rose :A∩B 13/49Appartenance, inclusion
intersection réunion exercices intersection d'ensembles On généralise l'intersection à plus d'ensembles : On définit l'intersection d'une famille de sous-ensembles(Ai)i?I d'un ensembleEcomme l'ensemble des élémentsx?Equi appartiennent à chacun des ensemblesAi. x?? i?IA i?? ?i?I,x?AiEXEMPLE: On considère trois disquesA,BetC:
A B C 14/49Appartenance, inclusion
intersection réunion exercices intersection d'ensembles On généralise l'intersection à plus d'ensembles : On définit l'intersection d'une famille de sous-ensembles(Ai)i?I d'un ensembleEcomme l'ensemble des élémentsx?Equi appartiennent à chacun des ensemblesAi. x?? i?IA i?? ?i?I,x?AiEXEMPLE: On considère trois disquesA,BetC:
A B CA B C en rose :A∩B 15/49Appartenance, inclusion
intersection réunion exercices intersection d'ensembles On généralise l'intersection à plus d'ensembles : On définit l'intersection d'une famille de sous-ensembles(Ai)i?I d'un ensembleEcomme l'ensemble des élémentsx?Equi appartiennent à chacun des ensemblesAi. x?? i?IA i?? ?i?I,x?AiEXEMPLE: On considère trois disquesA,BetC:
A B CA B CA B C en rose :A∩Bet en vertA∩B∩C 16/49Appartenance, inclusion
intersection réunion exercices intersection de deux ensembles On définit l'intersection de deux partiesAetBd'un ensembleE comme l'ensemble des élémentsx?Equi appartiennent à la fois àAet àB.Exemples :
R +∩R-= [-1;1]∩[0;3] = 17/49Appartenance, inclusion
intersection réunion exercices intersection de deux ensembles On définit l'intersection de deux partiesAetBd'un ensembleE comme l'ensemble des élémentsx?Equi appartiennent à la fois àAet àB.Exemples :
R +∩R-={0}[-1;1]∩[0;3] = 18/49Appartenance, inclusion
intersection réunion exercices intersection de deux ensembles On définit l'intersection de deux partiesAetBd'un ensembleE comme l'ensemble des élémentsx?Equi appartiennent à la fois àAet àB.Exemples :
R +∩R-={0}[-1;1]∩[0;3] = [0;1] 19/49Appartenance, inclusion
intersection réunion exercices intersection d'ensembles On généralise l'intersection à plus d'ensembles : On définit l'intersection d'une famille de sous-ensembles(Ai)i?I d'un ensembleEcomme l'ensemble des élémentsx?Equi appartiennent à chacun des ensemblesAi. x?? i?IA i?? ?i?I,x?AiEXEMPLE:
n?N?? -1 n;1n?= 20/49Appartenance, inclusion
intersection réunion exercices intersection d'ensembles On généralise l'intersection à plus d'ensembles : On définit l'intersection d'une famille de sous-ensembles(Ai)i?I d'un ensembleEcomme l'ensemble des élémentsx?Equi appartiennent à chacun des ensemblesAi. x?? i?IA i?? ?i?I,x?AiEXEMPLE:
n?N?? -1 n;1n?={0} 20/49Appartenance, inclusion
intersection réunion exercices Plan1Appartenance, inclusion
2intersection
3réunion
4complémentaire
5différence symétrique
6exercices
21/49Appartenance, inclusion
intersection réunion exercices réunion de deux ensembles On définit la réunion de deux partiesAetBd'un ensembleE comme l'ensemble des élémentsx?Equi appartiennent àA ou àB, le ou n'étant pas exclusif.EXEMPLE:
On considère deux disquesAetB:
A B 22/49Appartenance, inclusion
intersection réunion exercices réunion de deux ensembles On définit la réunion de deux partiesAetBd'un ensembleE comme l'ensemble des élémentsx?Equi appartiennent àA ou àB, le ou n'étant pas exclusif.EXEMPLE:
On considère deux disquesAetB:
A B A B A B en bleuA?B 23/49Appartenance, inclusion
intersection réunion exercices réunion d'ensembles On généralise la réunion à plus d'ensembles : On définit la réunion d'une famille de sous-ensembles(Ai)i?I d'un ensembleEcomme l'ensemble des élémentsx?Equi appartiennent à au moins l'un des ensemblesAi. x?? i?IA i?? ?i?I,x?AiEXEMPLE: On considère trois disquesA,BetC:
A B CA B CA B CEn bleuA?C
24/49Appartenance, inclusion
intersection réunion exercices réunion d'ensembles On généralise la réunion à plus d'ensembles : On définit la réunion d'une famille de sous-ensembles(Ai)i?I d'un ensembleEcomme l'ensemble des élémentsx?Equi appartiennent à au moins l'un des ensemblesAi. x?? i?IA i?? ?i?I,x?AiEXEMPLE: On considère trois disquesA,BetC:
A B CA B CA B CA B CEn bleuA?C; et en roseA?B?C
25/49Appartenance, inclusion
intersection réunion exercices réunion de deux ensembles On définit la réunion de deux partiesAetBd'un ensembleE comme l'ensemble des élémentsx?Equi appartiennent àA ou àB, le ou n'étant pas exclusif.EXEMPLES:
[-1;2]?[0;5] = 26/49Appartenance, inclusion
intersection réunion exercices réunion de deux ensembles On définit la réunion de deux partiesAetBd'un ensembleE comme l'ensemble des élémentsx?Equi appartiennent àAquotesdbs_dbs1.pdfusesText_1[PDF] exercices espagnol 4ème pdf
[PDF] exercices estimation ponctuelle avec correction
[PDF] exercices et correction de thermodynamique physique
[PDF] exercices et corriges de probabilite en pdf
[PDF] exercices et corrigés des travaux de fin d'exercice maroc
[PDF] exercices et corrigés sur amortissements provisions
[PDF] exercices et corrigés sur la paie 2016
[PDF] exercices et problèmes corrigés de physique nucleaire pdf
[PDF] exercices et problèmes corrigés de thermodynamique chimique nabih khadija
[PDF] exercices et problèmes de chimie générale
[PDF] exercices et problèmes de cryptographie dunod pdf
[PDF] exercices et problèmes de cryptographie pdf
[PDF] exercices et problèmes de radioactivité
[PDF] exercices et problèmes résolus de recherche opérationnelle tome 1 pdf
