 Chapitre I - Ensembles - cours et exercices
Chapitre I - Ensembles - cours et exercices
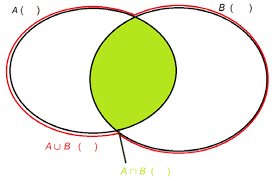
Ici les éléments intéressants sont ceux qui appartiennent à A ou à B : …………….. •. Intersection de deux ensembles inclusions possibles entre les ensembles : A ...
 1 Réunion intersection
1 Réunion intersection
produit carté- sien d'ensembles
 théorie des ensembles - une introduction
théorie des ensembles - une introduction
appartenance inclusion. 2 intersection. 3 réunion. 4 complémentaire. 5 différence symétrique. 6 exercices. 3 / 49. Page 4. Appartenance inclusion intersection.
 ensemble.pdf
ensemble.pdf
L'ensemble. {x
 1 Inclusion égalité
1 Inclusion égalité
intersection
 Chapitre 2 : ensembles
Chapitre 2 : ensembles
Inclusion ensemble des parties. On dit que l'ensemble A est inclus dans l 2 Union et intersection de deux ensembles. Dans tout ce qui suit
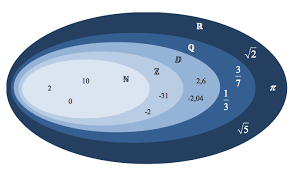 ENSEMBLES DE NOMBRES
ENSEMBLES DE NOMBRES
Intersections et unions d'intervalles : Définitions : -. L'intersection de deux ensembles A et B est l'ensemble des éléments qui Exercices conseillés En ...
 ´Enoncés des exercices
´Enoncés des exercices
Union intersection
 Corrigés des exercices Ensembles et applications
Corrigés des exercices Ensembles et applications
Pour montrer qu'une union est incluse dans un ensemble il suffit de montrer que chaque terme de l'union est inclus intersection.2 Autrement dit
 12.2 Exercices du chapitre 2 - 12.2.1 Tribus
12.2 Exercices du chapitre 2 - 12.2.1 Tribus
Si Σ est une tribu Σ est stable par union dénombrable et intersection dénombrable. L'ensemble K1 est donc compact car il est l'union de deux compacts. Comme.
 théorie des ensembles - une introduction
théorie des ensembles - une introduction
appartenance inclusion. 2 intersection. 3 réunion. 4 complémentaire. 5 différence symétrique. 6 exercices. 3 / 49. Page 4. Appartenance inclusion intersection.
 ensemble.pdf
ensemble.pdf
L'ensemble {x
 x ? A ou x ? B} est appelé lunion des ensembles A et B et est noté Exercice - Soient A B
x ? A ou x ? B} est appelé lunion des ensembles A et B et est noté Exercice - Soient A B
D des sous-ensembles d'un ensemble E.
 1 Réunion intersection
1 Réunion intersection
produit carté- sien d'ensembles
 ´Enoncés des exercices
´Enoncés des exercices
Union intersection
 Corrigés des exercices Ensembles et applications
Corrigés des exercices Ensembles et applications
Montrons que A ? B. Par définition de l'inclusion nous devons donc montrer un ensemble
 ENSEMBLES DE NOMBRES
ENSEMBLES DE NOMBRES
L'ensemble des nombres entiers naturels est noté ?. ?= 0;1;2;3;4. Exercices conseillés En devoir ... Intersections et unions d'intervalles :.
 Chapitre 2 : ensembles
Chapitre 2 : ensembles
double inclusion c'est à dire de montrer d'abord que A est inclus dans B
 1 Inclusion égalité
1 Inclusion égalité
intersection
 12.2 Exercices du chapitre 2 - 12.2.1 Tribus
12.2 Exercices du chapitre 2 - 12.2.1 Tribus
Corrigé 10 (Tribu engendrée). Soit E un ensemble. 1. Montrer qu'une intersection quelconque de tribus sur E est une tribu sur E.
 Exercices de mathématiques - Exo7
Exercices de mathématiques - Exo7
Montrer que les ensembles ci-dessous sont des espaces vectoriels (sur R) : Dans R3 donner un exemple de deux sous-espaces dont l'union n'est pas un ...
Corrigés des exercices
Ensembles et applications
N"hésitez pas à m"envoyer un mail si vous avez des questions. 11 Ensembles
Exercice 1. Echauffements I (?)
SoitEun ensemble. Que dire de deux sous-ensemblesAetBdeEtels queA[B= A\B?Solution de l"exercice 1.
Faire un dessin pour se convaincre que dans une telle situation,A=B. Montrons que c"est bien le cas. Pour ce faire, nous allons utiliser une technique très importante : la double inclusion. Le principe est d"utiliser l"équivalence suivante :A=Béquivaut àABetBA. On peut donc montrer le second pour en déduire le premier. Montrons queAB.Par définition de l"inclusion, nous devons donc montrer que :Pour touta2A;on a quea2B:
Soita2A. Par définition de l"union, an a alors quea2A[B. Or,A[B=A\B, donca2A\B. Par définition de l"intersection, on a alorsa2B.Conclusion :Pour touta2A, on a quea2B, doncAB.
Montrons queBA.L"énoncé est symétrique enAetB, etAB, donc BA. Conclusion :On a bien montré queABetBA, i.eA=B.Exercice 2. Echauffements II (?)
SoitEun ensemble et soientA,BetCtrois parties deEtelles queA[B=A[C etA\B=A\C. Montrer queB=C.Solution de l"exercice 2.
On procède à nouveau par double inclusion.1. vadim.lebovici@ens.fr 1 Montrons queBC.Soitb2B. On a alors queb2A[B. CommeA[B= A[C, on ab2A[C. Par définition de l"union, l y a alors deux possibilités :1er cas :b2C.on a ce qu"on voulait,b2C.
2nd cas :b2A.on a alorsb2A\B=A\Cet doncb2C. Dans tous les cas,
on a bienb2C.Conclusion :pour tousb2B, on ab2C, doncBC.
Montrons queCB.Le problème est symétrique enBetCetBC, donc CB.Conclusion.On a montré queBCetCB, doncB=C.
Exercice 3. Des parties (?)
SoientEetFdeux ensembles. Quelles relations d"inclusion y a-t-il entre :1.P(E[F)etP(E)[ P(F)?
2.P(E\F)etP(E)\ P(F)?
Solution de l"exercice 3.
1. Montrons queP(E)[ P(F) P(E[F).Pour montrer qu"une union est
incluse dans un ensemble, il suffit de montrer que chaque terme de l"union est inclus dans l"ensemble. Montrons queP(E) P(E[F).SoitA2 P(E), montrons queA2 P(E[F). Pour touta2A, on a quea2E, et donca2E[F, doncAE[F, i.e.A2 P(E[F). Ceci étant vrai pour tout élémentAdeP(E), on a bienP(E) P(E[F). Montrons queP(F) P(E[F).CommeEetFjouent des rôles symétriques et queP(E) P(E[F), on a égalementP(F) P(E[F). Conclusion :On a montré queP(E) P(E[F)etP(F) P(E[F), doncP(E)[ P(F) P(E[F):
Montrons qu"en général, on a pasP(E[F) P(E)[P(F).Pour cela, il faut que l"on exhibe un contre-exemple à cette proposition. PrenonsE=f0getF=f1g.On a alorsE[F=f0;1get donc :
P(E) =f;;f0gg;
P(F) =f;;f1gg;
P(E)[ P(F) =f;;f0g;f1gg;
P(E[F) =f;;f0g;f1g;f0;1gg;
ce qui montre bien que dans cet exempleP(E)[ P(F)6=P(E[F). 22.Montrons queP(E\F) =P(E)\ P(F).PourAun ensemble, on a que
AE\FéquivautAEetAF, par définition de l"intersection.2Autrement dit, on a équivalence entreA2 P(E\F)etA2 P(E)\ P(F), d"où le résultat.Exercice 4. Différence symétrique (???)
SoientAetBdeux parties d"un ensembleE. On appelledifférence symétrique deAetB, et on noteABl"ensemble défini par :
AB= (A[B)n(A\B):
1. Faire un dessin, puis calculerABpourA=f0;1;2;3getB=f2;3;4g.
2. Montrer queAB= (AnA\B)[(BnA\B).
3. Supposons queAB=A\B. Montrer queA=B=;.
4. SoitC2 P(E). Montrer queAB=ACsi, et seulement siB=C.
5. Résoudre l"équation d"inconnueX2 P(E),AX=;.
Solution de l"exercice 4.
1.De beaux dessins sont disponibles sur la page wikipédia de la différence symé-
trique. PourA=f0;1;2;3getB=f2;3;4g, on aAB=f0;1;4g:
2.Procédons par double-inclusion.
Montrons queAB(AnA\B)[(BnA\B).Soitx2AB. Par définition, x2A[B, doncx2Aoux2B. Supposons d"abord quex2A, l"autre cas étant symétrique. Par définition de la différence symétriquex62A\B, on a donc bien x2AnA\B. Par symétrie, six2B, on aurax2BnA\B. Conclusion :On a montré que pour toutx2AB, on ax2AnA\Boux2BnA\B, i.eAB(AnA\B)[(BnA\B).
Montrons que(AnA\B)[(BnA\B)AB.La preuve est similaire.3.SupposonsAB=A\B. Pour montrer queA=B=;, il nous suffit de
montrer queA=;, carAetBjouent des rôles symétriques. Montrons donc que A=;. Supposons par l"absurde qu"il existea2A. Deux cas sont alors possibles :1er cas :a2B.On aa2A\B=AB. Or, par définition de la différence
symétrique,a62A\B, une contradiction.2nd cas :a62B.On a alors quea62A\B. Puisquea2A, on a quea2A[B, et
donca2AB. Or,AB=A\B, donca2A\B, donca2B, une contradiction. Conclusion :Tous les cas mènent à une contradiction, c"est donc qu"il n"existe pasdea2A, et doncA=;.2. Si vous n"êtes pas convaincu, prouvez-le, en prenant des élémentsa2Aet en montrant
l"équivalence. 34.SiB=C, alors il est clair queAB=AC. Supposons maintenantAB=
AC, et montrons queB=C. A nouveau, nous allons procéder par double inclusion. Montrons queBC.Soitb2B. Il y a plusieurs possibilités :1. Sib2A, alors il est dansA\B, et ne peut donc pas être dansAB. Comme
AB=ACpar hypothèse,b62AC. Commeb2A, c"est qu"il doit être dansA\C, etb2C.2. Sib62A, alors il est dansA[BnA\B=AB=AC. Doncb2A[C,
maisb62A, doncb2C. Dans tous les cas,b2C. Ceci étant vrai pour tousb2B, on a bienBC. Montrons queCB.L"énonce est symétrique enBetC, etBC.Conclusion :B=C.
5.On a que
AA=A[AnA\A=AnA=;;
doncAest solution de l"équation. De plus, n"importe quelle partieXdeEsatisfaisant AX=;satisferaitAX=AA. Or, par la question précédente, on a dans ce casX=A. Conclusion :La seule solution de l"équation est la partieA.2 Applications
Exercice 5. Gammes sur l"injectivité et la surjectivité (?) SoientX,YetZtrois ensembles. Soientf:X!Yetg:Y!Zdeux applications.Montrer que :
1. Injectivité
(a) Sifetgsont injectives, alorsgfl"est aussi. (b) La relation de subpotence est transitive, i.e. siX4YetY4Zalors X4Z. (c) Sigfest injective, alorsfest injective. (d) Donner un exemple oùgfest injective et oùgne l"est pas.2. Surjectivité
(a) Sifetgsont surjectives, alorsgfl"est aussi. (b) La relation de surpotence est transitive. (c) Sigfest surjective, alorsgest surjective. (d) Donner un exemple oùgfest surjective et oùfne l"est pas.3. Sigfest surjective etgest injective, alorsfest surjective.
4. Sigfest injective etfest surjective, alorsgest injective.
45. La relation d"équipotence est transitive.
Solution de l"exercice 5.
1. (a)Supposons quefetgsont injectives. Montrons quegfest injective. Soient
doncx2Xetx02Xtels quegf(x) =gf(x0)et montrons quex=x0. Comme gest injective, on a doncf(x) =f(x0). Commefest injective, on ax=x0. Conclusion :Pour tousx2Xetx02Xtels quegf(x) =gf(x0), on ax=x0, i.egfest injective.1. (b)Supposons queX4YetY4Z, i.e il existe une injectionf:X!Yet
une injectiong:Y!Z. On pose alorsh=gf:X!Z. Par la question 1.(a), cette application est injective carfetgle sont. Par définition, on a doncX4Z.1. (c)Supposons quegfest injective. Montrons quefest injective. Soient donc
x2Xetx02Xtels quef(x) =f(x0)et montrons quex=x0. Commef(x) =f(x0) on peut appliquergpour obtenir queg(f(x)) =g(f(x0)).3Or,gfest injective, ceci implique doncx=x0. Conclusion :Pour tousx2Xetx02Xtels quef(x) =f(x0), on ax=x0, i.ef est injective.1. (d)On pose :
f:f0;1g ! f0;1;2g x7!x que l"on aurait pu écrire aussi moins efficacement : f:f0;1g ! f0;1;2g 07!0 17!1 ainsi que : g:f0;1;2g ! f0;1g 07!0 17!1 27!1:On peut alors facilement vérifier que :
gf:f0;1g ! f0;1g 07!0 17!1 Cette application est clairement injective (le vérifier si ce n"est pas clair). En re-vanche,gne l"est pas :g(1) =g(2)alors que16= 2.3. Noter que ceci est vrai parce que l"image d"un élément par une application est unique.
52. (a)Supposons quefetgsont surjectives. Montrons quegfl"est aussi, i.e
que pour toutz2Z, il existex2Xtel quegf(x) =z. Soitz2Z. Commegest surjective, il existey2Ytel quez=g(y). Comme de plusfest surjective, il existe x2Xtel quey=f(x). On a alorsz=g(y) =g(f(x)) =gf(x). Conclusion :Pour toutz2Z, il existex2Xtel quez=gf(x), i.egfest surjective.2. (b)S"inspirer de 1. (b).
2. (c)Supposons quegfest surjective. Montrons quegl"est. Soitz2Z. Comme
gfest surjective, il existex2Xtel quez=gf(x).On posealorsy=f(x). On a bienz=gf(x) =g(f(x)) =g(y). Conclusion :On a montré que pour toutz2Z, il existey2Ytel quez=g(y), i.e gest surjective.2. (d)On pose :
f:f0;1g ! f0;1;2g 07!0 17!1 ainsi que : g:f0;1;2g ! f0;1g 07!0 17!1 27!1:On peut alors facilement vérifier que :
gf:f0;1g ! f0;1g 07!0 17!1 On a alors quegfest clairement surjective alors quefne l"est pas, puisque2n"est l"image d"aucun élément def0;1gparf.3.Montrons quefest surjective. Soity2Y. On posez=g(y)2Z. Commez2Z,
et quegfest surjective, il existex2Xtel quez=gf(x), i.eg(y) =g(f(x)).Comme de plusgest injective,y=f(x).
Conclusion :Pour touty2Y, il existex2Xtel quey=f(x), i.efest surjective.4.Montrons quegest injective. Soienty2Yety02Ytels queg(y) =g(y0),
montrons quey=y0. Commefest surjective, il existex2Xtel quey=f(x)et 6 x02Xtel quey0=f(x0). On a alors
gf(x) =g(f(x)) =g(y) =g(y0) =g(f(x0)) =gf(x0): Or,gfest injective, doncx=x0. Ceci implique quef(x) =f(x0), i.ey=y0. Conclusion :Pour tousy2Yety02Ytels queg(y) =g(y0), on ay=y0, i.egest injective.5.Utiliser les questions 1.(a) et 2.(a) pour montrer qu"une composée de bijections
est une bijection puis s"inspirer de la question 1.(b). Exercice 6. Une propriété en entraîne une autre (??) SoitEun ensemble et soitf:P(E)!R. On suppose que pour toutes partiesAetBdisjointes4deE, on af(A[B) =f(A) +f(B).
1. Montrer quef(;) = 0.
2. Montrer que pour toutes partiesAetBdeEtelles queAB, on af(BnA) =
f(B)f(A).3. Montrer que pour toutes partiesAetBdeE, on af(A[B) =f(A)+f(B)
f(A\B).Solution de l"exercice 6.
1.Comme; \ ;=;(i.e le vide est disjoint de lui-même) et que; [ ;=;, on a
f(;) =f(;) +f(;) = 2f(;). Ceci implique doncf(;) = 0.2.SoientAetBdeux parties deEtelles queAB. On peut décomposer :
B= (BnA)[Aavec(BnA)\A=;(le montrer si ce n"est pas clair). On a alors f(B) =f(BnA) +f(A), d"où le résultat.3.On peut décomposerA[Ben trois parties disjointes :
A[B= (AnA\B)[(BnA\B)[A\B4. i.e. telle queA\B=;
7 et ainsi calculer : f(A[B) =f((AnA\B)[(BnA\B)[A\B) =f(AnA\B) +f((BnA\B)[A\B) =f(AnA\B) +f(BnA\B) +f(A\B) =f(A)f(A\B) +f(B)f(A\B) +f(A\B) =f(A) +f(B)f(A\B):Exercice 7. Fonctions caractéristiques (???)
SoitAune partie d"un ensembleE. On lui associe l"application suivante : 1A:E! f0;1g
x7!(1six2A;
0sinon:
1. (?) Montrer que pour toutes partiesAetBdeE, les fonctions suivantes5sont
les fonctions indicatrices de parties deEque l"on déterminera : (a)1B1A, siAB. (b)1A1B. (c)1A+1B, siAetBsont disjointes. (d)1A+1B1A\B.2. (???) Montrer que pour toutes partiesAetBdeE, on a On noteF(E;f0;1g)
l"ensemble des applications deEdansf0;1g. Montrer que l"application : f:P(E)! F(E;f0;1g) A7!1A est une bijection. 63. (????)Application.Résoudre la question 4 de l"exercice 4 en ne faisant que des
calculs de fonctions caractéristiques.Solution de l"exercice 7.
1. (a), (b), (c)On a1BnA=1B1AsiAB,1A\B=1A1B, et1A[B=1A+1B
siAetBsont disjointes. Les trois démonstrations étant similaires, on traite intégra-lement la première, et laissons les autres au lecteur ou à la lectrice. Soient doncA5. La somme de deux fonctions est définie ainsi : pourx2E,(1A+1B)(x) =1A(x) +1B(x),
et les autres opérations sont définies de manière similaire.6. L"injectivité implique en particulier que, pour toutes partiesAetBdeE, on aA=Bsi, et
seulement si1A=1B. 8 etBdeux parties deEtelles queAB. On souhaite montrer que pour toutx2E, 1BnA(x) =1B(x)1A(x). Soitx2E.
1er cas :x2BnA.On a alors1BnA(x) = 1. Commex2B, on a1B(x) = 1et
commex62A,1A(x) = 0. Ainsi, on a bien :1B(x)1A(x) = 10 = 1 =1BnA(x).2nd cas :x62BnA.On a alors que1BnA(x) = 0. De plus, il y a alors deux possibi-
lités : ou bienx62B, ou bienx2A. Six62B, alors1B(x) = 0etx62AcarAB, donc aussi1A(x) = 0. Ainsi :1B(x)1A(x) = 00 = 0 =1BnA(x). Six2A, alors aussix2BcarAB. On aura donc1B(x)1A(x) = 11 = 0 =1BnA(x). Conclusion :dans tous les cas, on a bien montré que pour toutx2E,1BnA(x) = 1B(x)1A(x), i.e1BnA=1B1A.
1. (d)On a1A[B=1A+1B1A\B. Pour le montrer, on utilise les questions
précédentes et le fait que l"on peut décomposerA[Ben trois parties disjointes :A[B= (AnA\B)[(BnA\B)[A\B:
2.On doit montrer quefest injective et surjective. Commençons par l"injectivité.
On doit montrer que pour toutes partiesA2 P(E)etA02 P(E)telles que1A=1A0 on aA=A0. Soient doncA2 P(E)etA02 P(E)telles que1A=1A0. Procédons par double inclusion. Soita2A. On a alors1A(a) = 1. Or1A0(a) =1A(a) = 1donc a2A0par définition de1A0. Ainsi,AA0. Par symétrie, on a aussi queA0A. Conclusion :on a montré que pour toutes partiesA2 P(E)etA02 P(E)telles que 1A=1A0on aA=A0, i.e.fest injective.
Montrons quefest surjective. Soit2 F(E;f0;1g). PosonsA=fx2Ej(x) = 1g 2 P(E):
Montrons que=1A=f(A). Soitx2E. Six2A, alors1A(x) = 1 =(x)par définition deAet de1A. Six62A, alors1A(x) =(x)par définition deAet de1A. Conclusion :on a montré que pour tout2 F(E;f0;1g), il existeA2 P(E)telle que=f(A), i.efest surjective.3.SoientA;BetCtrois parties deE. Montrons queAB=ACsi, et seulement
siB=C. Puisquefest injective, on a que pour toutes partiesDetD0deEque 1D=1D0,D=D0:
On a donc que
AB=ACéquivaut à
1AB=1AC:
9De plus, par la question 1), on a :
1AB=1(A[B)n(A\B)
=1A[B1A1B =1A+1B21A1B =12A+12B21A1B = (1A1B)2: où la troisième égalité vient du fait que1Aet1Bsont à valeurs dansf0;1get que 02= 0et11= 1. Ainsi,AB=ACéquivaut à :
(1A1B)2= (1A1C)2: Attention, ceci n"est équivalent à1A1B=1A1Cque si les deux côtés de cette dernière égalité sont de même signe. En fait, c"est toujours le cas. En effet, six2A, alors1A(x) = 1et1A(x)1B(x)0car1B(x)2 f0;1g, idem on a 1 A(x)1C(x)0. Six62A, alors1A(x) = 0et1A(x)1B(x)0car1B(x)2 f0;1g et encore1A(x)1C(x)0. On a donc bien dans tous les cas : 1A1B=1A1C:
Ce qui équivaut à :
1 B=1C; et, commefest injective, ceci équivaut à : B=C:Exercice 8. Un classique (?)
SoitEun ensemble. Montrer qu"il n"existe pas de surjectionEdansP(E).Solution de l"exercice 8.
Soitf:E! P(E). On pose alors :
A=fx2Ejx62f(x)g 2 P(E);
qui a bien un sens puisquef(x)E(c"est une partie deE). Montrons queAn"a pas d"antécédent parf. Supposons par l"absurde qu"il existez2Etel queA=f(z).On a alors deux possibilités :
- ou bienz2Aet alorsz2f(z), doncz62Apar définition deA, ce qui est absurde, - ou bienz62Aet alorsz62f(z), doncz2Apar définition deA, ce qui est absurde. Dans tous les cas, l"existence d"un antécédent deAparfest absurde, doncAn"a pas d"antécédent etfn"est pas surjective. 10quotesdbs_dbs1.pdfusesText_1[PDF] exercices espagnol 4ème pdf
[PDF] exercices estimation ponctuelle avec correction
[PDF] exercices et correction de thermodynamique physique
[PDF] exercices et corriges de probabilite en pdf
[PDF] exercices et corrigés des travaux de fin d'exercice maroc
[PDF] exercices et corrigés sur amortissements provisions
[PDF] exercices et corrigés sur la paie 2016
[PDF] exercices et problèmes corrigés de physique nucleaire pdf
[PDF] exercices et problèmes corrigés de thermodynamique chimique nabih khadija
[PDF] exercices et problèmes de chimie générale
[PDF] exercices et problèmes de cryptographie dunod pdf
[PDF] exercices et problèmes de cryptographie pdf
[PDF] exercices et problèmes de radioactivité
[PDF] exercices et problèmes résolus de recherche opérationnelle tome 1 pdf
