 Chapitre I - Ensembles - cours et exercices
Chapitre I - Ensembles - cours et exercices
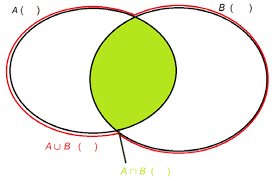
Ici les éléments intéressants sont ceux qui appartiennent à A ou à B : …………….. •. Intersection de deux ensembles inclusions possibles entre les ensembles : A ...
 1 Réunion intersection
1 Réunion intersection
produit carté- sien d'ensembles
 théorie des ensembles - une introduction
théorie des ensembles - une introduction
appartenance inclusion. 2 intersection. 3 réunion. 4 complémentaire. 5 différence symétrique. 6 exercices. 3 / 49. Page 4. Appartenance inclusion intersection.
 ensemble.pdf
ensemble.pdf
L'ensemble. {x
 1 Inclusion égalité
1 Inclusion égalité
intersection
 Chapitre 2 : ensembles
Chapitre 2 : ensembles
Inclusion ensemble des parties. On dit que l'ensemble A est inclus dans l 2 Union et intersection de deux ensembles. Dans tout ce qui suit
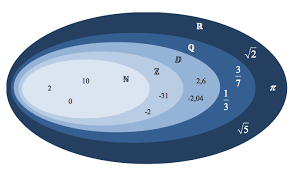 ENSEMBLES DE NOMBRES
ENSEMBLES DE NOMBRES
Intersections et unions d'intervalles : Définitions : -. L'intersection de deux ensembles A et B est l'ensemble des éléments qui Exercices conseillés En ...
 ´Enoncés des exercices
´Enoncés des exercices
Union intersection
 Corrigés des exercices Ensembles et applications
Corrigés des exercices Ensembles et applications
Pour montrer qu'une union est incluse dans un ensemble il suffit de montrer que chaque terme de l'union est inclus intersection.2 Autrement dit
 12.2 Exercices du chapitre 2 - 12.2.1 Tribus
12.2 Exercices du chapitre 2 - 12.2.1 Tribus
Si Σ est une tribu Σ est stable par union dénombrable et intersection dénombrable. L'ensemble K1 est donc compact car il est l'union de deux compacts. Comme.
 théorie des ensembles - une introduction
théorie des ensembles - une introduction
appartenance inclusion. 2 intersection. 3 réunion. 4 complémentaire. 5 différence symétrique. 6 exercices. 3 / 49. Page 4. Appartenance inclusion intersection.
 ensemble.pdf
ensemble.pdf
L'ensemble {x
 x ? A ou x ? B} est appelé lunion des ensembles A et B et est noté Exercice - Soient A B
x ? A ou x ? B} est appelé lunion des ensembles A et B et est noté Exercice - Soient A B
D des sous-ensembles d'un ensemble E.
 1 Réunion intersection
1 Réunion intersection
produit carté- sien d'ensembles
 ´Enoncés des exercices
´Enoncés des exercices
Union intersection
 Corrigés des exercices Ensembles et applications
Corrigés des exercices Ensembles et applications
Montrons que A ? B. Par définition de l'inclusion nous devons donc montrer un ensemble
 ENSEMBLES DE NOMBRES
ENSEMBLES DE NOMBRES
L'ensemble des nombres entiers naturels est noté ?. ?= 0;1;2;3;4. Exercices conseillés En devoir ... Intersections et unions d'intervalles :.
 Chapitre 2 : ensembles
Chapitre 2 : ensembles
double inclusion c'est à dire de montrer d'abord que A est inclus dans B
 1 Inclusion égalité
1 Inclusion égalité
intersection
 12.2 Exercices du chapitre 2 - 12.2.1 Tribus
12.2 Exercices du chapitre 2 - 12.2.1 Tribus
Corrigé 10 (Tribu engendrée). Soit E un ensemble. 1. Montrer qu'une intersection quelconque de tribus sur E est une tribu sur E.
 Exercices de mathématiques - Exo7
Exercices de mathématiques - Exo7
Montrer que les ensembles ci-dessous sont des espaces vectoriels (sur R) : Dans R3 donner un exemple de deux sous-espaces dont l'union n'est pas un ...
12.2 Exercices du chapitre 2
12.2.1 Tribus
Corrig´e 9 (Caract´erisation d"une tribu)
SoitEun ensemble.
1. SoitTune partie deP(E) stable par union d´enombrable, stable par passage au compl´ementaire et
t.q.∅ ?T. Montrer queTest une tribu, c"est-`a-dire qu"elle v´erifie aussiE?Tet qu"elle est stable
par intersection d´enombrable. -------------corrig´e-------------- •E?TcarE=∅cet queTest stable par passage au compl´ementaire. •Test stable par intersection d´enombrable car, si (An)?T, on a (∩n?NAn)c=?n?NAcn?T(car Test stable par passage au compl´ementaire et par union d´enombrable) et donc∩n?NAn?T (carTest stable par passage au compl´ementaire).2. L"ensemble des parties finies deEest-il une tribu ?
-------------corrig´e-------------- •SiEest fini, l"ensemble des parties finies deEest une tribu, c"est la tribuP(E).•SiEest infini, l"ensemble des parties finies deEn"est pas une tribu, car il n"est pas stable par
passage au compl´ementaire (le compl´ementaire d"une partie finie est infinie...).Corrig´e 10 (Tribu engendr´ee)
SoitEun ensemble.
1. Montrer qu"une intersection quelconque de tribus surEest une tribu surE.
-------------corrig´e-------------- Soit (Ti)i?Iune famille de tribus surI(Iest un ensemble quelconque). On poseT={A?E; A?Tipour touti?I}(Test bien l"intersection des tribusTi,i?I). On montre queTest une tribu : • ∅ ?Tcar∅ ?Tipour touti?I. •Test stable par compl´ementaire car, siA?T, on aA?Tipour touti?I, doncAc?Ti pour touti?I(carTiest stable par passage au compl´ementaire), doncAc?T. •Test stable par union d´enombrable car, si (An)n?N?T, on aAn?Tipour touti?Iet toutn?Ndonc?n?NAn?Tipour touti?Iet toutn?N(carTiest stable par union d´enombrable), donc?n?NAn?T, d"apr`es l"exercice pr´ec´edent, on en d´eduit queTest une tribu. 2832. SoitA ? P(E). On noteTAl"intersection de toutes les tribus surEcontenantA(une partie
deEappartient donc `aTAsi et seulement si elle appartient `a toutes les tribus contenantA, on remarquera qu"il y a toujours au moins une tribu contenantA, c"est la tribuP(E)). Montrer que T Aest la plus petite des tribus contenantA(c"est la tribu engendr´ee parA). -------------corrig´e--------------D"apr`es la question pr´ec´edente,TAest bien une tribu. La d´efinition deTAdonne que toute tribu
contenantAdoit contenirTA.TAest donc la plus petite tribu contenantA.3. SoientAetB ? P(E) etTA,TBles tribus engendr´ees parAetB. Montrer que siA ? Balors
T A?TB. -------------corrig´e-------------- T Best une tribu contenantB, donc contenantA. DoncTA?TB.Corrig´e 11 (Exemples de tribus)
1. Tribu trace
(a) SoitTune tribu sur un ensembleEetF?E. Montrer queTF={A∩F, A? T }est une tribu surF(tribu trace deTsurF). -------------corrig´e-------------- • ∅ ? TFcar∅=∅ ∩Fet∅ ? T.
•SoitA? TF. Il existeB? Tt.q.A=B∩F. On a doncF\A= (E\B)∩F? TFcar E\B? T.TFest donc stable par passage au compl´ementaire. •Soit (An)n?N? TF. Pour toutn?N, il existeBn?Tt.q.An=Bn∩F. On a donc?n?NAn= (?n?NBn)∩F? TFcar?n?NBn? T.TFest donc stable par union d´enombrable. Ceci est suffisant pour dire queTFest une tribu surF. (b) SiEest un espace topologique etT=B(E) (B(E) est la tribu bor´elienne deE), montrer que la tribu trace surF, not´eeTF, est la tribu engendr´ee par la topologie trace surF(tribu bor´elienne deF, not´eeB(F)). [Montrer queB(F)?TF. Pour montrer queTF? B(F), consid´ererC={A? P(E);A∩F? B(F)}et montrer queCest une tribu (surE) contenant les ouverts deE.] SiFest un bor´elien deE, montrer queTFest ´egale `a l"ensemble des bor´eliens deEcontenus dansF. -------------corrig´e-------------- On noteOFl"ensemble des ouverts deF, etOEl"ensemble des ouverts deE. Par d´efinition de la topologie trace,OF={O∩F,O? OE}. CommeOE? B(E), on aOF?TF={B∩F,B? B(E)}(Noter queTF=B(E)F, avec les notations de la question pr´ec´edente). On en d´eduit queB(F)?TFcarTFest une tribu surFcontenantOFqui engendreB(F).
284On montre maintenant queTF? B(F). On poseC={A? P(E);A∩F? B(F)}.∅ ? C car∅ ∩F=∅ ? B(F).Cest stable par passage au compl´ementaire car, siA? C, on a (E\A)∩F=F\A=F\(A∩F)? B(F), donc (E\A)? C. Enfin, pour montrer queCest stable par union d´enombrable, soit (An)n?N? C, on a (?n?NAn)∩F=?n?N(An∩F)? B(F), ce qui donne?n?NAn? Cet la stabilit´e deCpar union d´enombrable.Cest donc une tribu. Il est clair queOE? Ccar siO? OE, on aO∩F? OF? B(F). La tribuCcontientOE, ce qui prouve queCcontientB(E) et donc queA∩F? B(F) pour toutA? B(E). Ceci donne exactementTF? B(F). On a bien montr´e finalement queTF=B(F) (on rappelle que T F=B(E)F, avec les notations de la question pr´ec´edente). On suppose maintenant queFest un bor´elien deE, c"est-`a-dire queF? B(E). On a alors T F? B(E) (carA∩F? B(E) siA? B(E)). Puis, soitA?Ft.q.A? B(E), on peut ´ecrire A=A∩F, doncA?TF. On a bien montr´e queTF={A?F;A? B(E)}.
2. SoitEun ensemble infini etS={{x},x?E}. D´eterminer la tribu engendr´ee parS(distinguer les
casEd´enombrable et non d´enombrable). -------------corrig´e--------------On noteT(S) la tribu engendr´ee parS.
•On suppose queEest au plus d´enombrable (c"est-`a-dire dire fini ou d´enombrable). D"apr`es
la stabilit´e deT(S) par union d´enombrable, la tribuT(S) doit contenir toutes les parties au plus d´enombrables. Comme toutes les parties deEsont au plus d´enombrables, on en d´eduitT(S) =P(E).
•On suppose maintenant queEest infini non d´enombrable. On noteAl"ensemble des parties de Eau plus d´enombrables etB={Ac,A? A}. D"apr`es la stabilit´e deT(S) par union d´enom- brable, la tribuT(S) doit contenirA. Par stabilit´e deT(S) par passage au compl´ementaire,T(S) doit aussi contenirB.
on va montrer maintenant queA ? Best une tribu (on en d´eduit queT(S) =A ? B). On a ∅ ? A ? A ? Bet il est clair queA ? Best stable par passage au compl´ementaire (carA? A impliqueAc? BetA? BimpliqueAc? A). Enfin, si (An)n?N? A ? B, on distingue 2 cas :1er cas. SiAn? Apour toutn?N, on a alors?n?NAn? A ? A ? B.
2eme cas. Si il existen?Nt.q.An? Bon a alorsAcn? A, doncAcnest au plus d´enombrable
et (?p?NAp)c=∩p?NAcp?Acnest aussi au plus d´enombrable,ce qui donne (?p?NAp)c? Aet p?NAp? B ? A ? B. On a bien montr´e que?n?NAn? A ? B. Ce qui prouve la stabilit´e par union d´enombrable de A ? B. Finalement,A ? Best donc une tribu contenantSet contenu dansT(S), ceci donneT(S) =A ? B.
Corrig´e 12 (Tribu image)
SoientEetFdes ensembles. PourA ? P(E) (resp.P(F)) on noteT(A) la tribu deE(resp.F) engendr´ee parA.Soitf:E→Fune application.
2851. Montrer que siT?est une tribu surF, alorsf-1(T?) ={f-1(B);B? T?}est une tribu surE
(tribu image r´eciproque). -------------corrig´e-------------- On d´emontre quef-1(T?) est une tribu surEen remarquant quef-1(∅) =∅,E\f-1(A) = f -1(F\A) (pour toutA?F) etf-1(?n?NAn) =?n?Nf-1(An) (pour toute suite (An)n?N? P(F)).2. Montrer que siTest une tribu surE, alorsT?={B?F;f-1(B)? T }est une tribu surF(tribu
image directe). -------------corrig´e-------------- Ici aussi, on montre queT?est une tribu surFen remarquant quef-1(∅) =∅,f-1(F\A) = E\f-1(A) (pour toutA?F) etf-1(?n?NAn) =?n?Nf-1(An) (pour toute suite (An)n?N? P(F)).Noter que, en g´en´eral,{f(B),B? T }n"est pas une tribu surF(par exemple, sifest non surjective,
F?? {f(B),B? T }).
3. Montrer que pour tout ensembleCde parties deFon a :T(f-1(C)) =f-1(T(C)). [Montrer que
T(f-1(C))?f-1(T(C)). Puis, pour montrer quef-1(T(C))?T(f-1(C)), montrer queT={G?F;f-1(G)?T(f-1(C))}est une tribu contenantC.]
-------------corrig´e-------------- f -1(T(C)) est une tribu surE(d"apr`es la premi`ere question) contenantf-1(C) (carT(C)? C), elle contient doncT(f-1(C)), ce qui donnef-1(T(C))?T(f-1(C)). Pour montrer l"inclusion inverse, c"est-`a-diref-1(T(C))?T(f-1(C)). On poseT={G?F; f -1(G)?T(f-1(C))}. On montre d"abord queTest une tribu : • ∅ ?Tcarf-1(∅) =∅ ?T(f-1(C)) •Test stable par passage au compl´ementaire car, siA?T, on af-1(A)?T(f-1(C)) et f -1(F\A) =E\f-1(A)?T(f-1(C)), donc (F\A)?T. •Test stable par union d´enombrable car, si (An)n?N?T, on af-1(An)?T(f-1(C)) pour toutn?Netf-1(?n?NAn) =?n?Nf-1(An)?T(f-1(C)), donc?n?NAn?T. On a bien montr´e queTest une tribu. Il est imm´ediat queT? C(carf-1(B)?T(f-1(C)) pour toutB? C). On en d´eduit queTcontientT(C), c"est-`a-dire quef-1(B)?T(f-1(C)) pour tout B?T(C). Ceci signifie exactement quef-1(T(C))?T(f-1(C)). Les 2 inclusions nous donnent bienf-1(T(C)) =T(f-1(C)).Corrig´e 13 (π-syst`eme,λ-syst`eme)
Soit Ω un ensemble etF ? P(Ω).
1. Montrer queFest une tribu si et seulement siFest unπ-syst`eme (c"est-`a-dire stable par intersection
finie) et unλ-syst`eme (c"est-`a-dire queFest stable par union d´enombrable croissante, Ω? Fet
A\B? FsiA,B? FavecB?A).
2862. On suppose queFest unλ-syst`eme. SoitC? F. On poseG={B?Ω t.q.C∩B? F}. Montrer
queGest unλ-syst`eme. -------------corrig´e--------------En attente
Corrig´e 14 (Tribu bor´elienne deR2)
On noteTla tribu (surR2) engendr´ee par{A×B;A, B? B(R)}. On va montrer ici queT=B(R2).1. Montrer que tout ouvert deR2est r´eunion au plus d´enombrable de produits d"intervalles ouverts de
R. [S"inspirer d"une d´emonstration analogue faite pourRau lieu deR2.] En d´eduire queB(R2)?T. -------------corrig´e--------------On s"inspire ici de la d´emonstration du lemme 2.1 (on peut reprendre aussi la d´emonstration de
l"exercice 15). SoitOun ouvert deR2. Pour toutx= (x1,x2)t?O, il exister >0 t.q. ]x1-r,x1+r[×]x2- r,x2+r[?O. Comme les rationnels sont denses dansR, on peut trouvery1?Q∩]x1-r,x1[,
z1?Q∩]x1,x1+r[,y2?Q∩]x2-r,x2[ etz2?Q∩]x2,x2+r[. On a doncx?]y1,z1[×]y2,z2[?O.
On note alorsI={(y1,z1,y2,z2)?Q4; ]y1,z1[×]y2,z2[)?O}. Pour toutx?O, il existe donc (y1,z1,y2,z2)?It.q.x?]y1,z1[×]y2,z2[. On en d´eduit queO=?(y1,z1,y2,z2)?I]y1,z1[×]y2,z2[.
CommeIest au plus d´enombrable (carQ4est d´enombrable), on en d´eduit queO?T. On a ainsimontr´e queTest une tribu contenant tous les ouverts deR2, et donc contenant la tribu engendr´ee
par les ouverts deR2(c"est-`a-direB(R2)). Donc,B(R2)?T.2. SoitAun ouvert deRetT1={B? B(R);A×B? B(R2)}. Montrer queT1est une tribu (surR)
contenant les ouverts (deR). En d´eduire queT1=B(R). -------------corrig´e-------------- • ∅ ?T1carA× ∅=∅ ? B(R2). •On montre ici queT1est stable par passage au compl´ementaire. SoitB?T1, on a doncBc? B(R) etA×Bc=A×(R\B) = (A×R)\(A×B). Or, (A×R) est un ouvert deR2(carAetRsont des ouverts deR), on a donc (A×R)? B(R2). D"autre part, (A×B)? B(R2) (carB?T1). Donc,A×Bc= (A×R)\(A×B)? B(R2). Ce qui prouve queBc?T1et donc queT1est stable par passage au compl´ementaire. •Enfin,T1est stable par union d´enombrable. En effet, si (Bn)n?N?T1, on aA×(?n?NBn) = n?NA×Bn? B(R2) (carA×Bn? B(R2) pour toutn?N). Donc,?n?NBn?T1. On a donc montr´e queT1est une tribu, il reste `a montrer queT1contient les ouverts deR. SoitBun ouvert deR. On a doncB? B(R) et, commeA×Best un ouvert deR2, on aA×B? B(R2). On a doncB?T1.
287T
1est donc une tribu contenant les ouverts deR, donc contenantB(R). Donc,T1=B(R).
La cons´equence de cette question est donc :
Aouvert deRetB? B(R)?A×B? B(R2).(12.4)
3. SoitB? B(R) etT2={A? B(R);A×B? B(R2)}. Montrer queT2=B(R).
-------------corrig´e-------------- On commence par remarquer que la question pr´ec´edente donne queT2contient les ouverts deR. En effet, soitAun ouvert deR, la propri´et´e (12.4) donneA×B? B(R2), et doncA?T2. On montre maintenant queT2est une tribu (on en d´eduira queT2=B(R)). • ∅ ?T2car∅ ×B=∅ ? B(R2). •On montre ici queT2est stable par passage au compl´ementaire. SoitA?T2, on aAc? B(R) etAc×B= (R×B)\(A×B). La propri´et´e (12.4) donne (R×B)? B(R2) carRest un ouvert deR. D"autre part, (A×B)? B(R2) (carA?T2). Donc,Ac×B? B(R2). Ce qui prouve queAc?T2et donc queT2est stable par passage au compl´ementaire. •Enfin,T2est stable par union d´enombrable. En effet, si (An)n?N?T2, on a (?n?NAn)×B= n?N(An×B)? B(R2) (carAn×B? B(R2) pour toutn?N). Donc,?n?NAn?T2. T2est donc une tribu (surR) contenant les ouverts deR, ce qui prouve queT2? B(R) et donc,
finalement,T2=B(R).4. Montrer queT? B(R2) (et donc queT=B(R2)).
-------------corrig´e--------------La question pr´ec´edente donne :
A,B? B(R)?A×B? B(R2).
On a donc{A×B;A, B? B(R)} ? B(R2). On en d´eduitT? B(R2). Avec la question 1, on a finalementT=B(R2).Corrig´e 15 (Tribu bor´elienne surRN)
1. Montrer que la tribu bor´elienne deRNest ´egale `a celle engendr´ee par l"ensemble de toutes les boules
ouvertes deRN. [On pourra montrer d"abord que tout ouvert deRNest r´eunion d´enombrable de boules ouvertes deRN.] -------------corrig´e-------------- SoitTla tribu engendr´ee par l"ensemble de toutes les boules ouvertes deRN. Comme les boules ouvertes sont des ouverts, on aT? B(RN). 288On montre maintenant l"inclusion inverse, c"est-`a-direB(RN)?T. SoitOun ouvert deRN. Pour toutx?O, il exister >0 t.q.B(x,r)?O(o`uB(x,r) d´eisgne la boule ouverte de centrexet rayonr). Comme les rationnels sont densesR, on peut donc trouvery?QNets?Q?+={t?Q; t >0}, t.q.x?B(y,s)?O. On note alorsI={(y,s)?QN×Q?+;B(y,s)?O}. On a alors O=?(y,s)?IB(y,s). CommeIest au plus d´enombrable (carQN+1est d´enombrable), on en d´eduit queO?Tet donc queB(RN)?T(carTest une tribu contenant tous les ouverts).
Le raisonnement pr´ec´edent montre mˆeme queB(RN) est aussi la tribu engendr´ee par l"ensemble
des boules ouvertes `a rayons rationnels et centre `a coordonn´ees rationnelles.2. Montrer que la tribu bor´elienne deRNest ´egale `a celle engendr´ee par l"ensemble des produits
d"intervalles ouverts `a extr´emit´es rationnelles. -------------corrig´e--------------On reprend le mˆeme raisonnement que dans la question pr´ec´edente en rempla¸cantB(x,r) par
P(x,r) =?N
i=1]xi-r,xi+r[, avecx= (x1,...,xN)t.3. Montrer que la tribu bor´elienne deRest engendr´ee par les intervalles ]a,b] o`ua,b?R,a < b.
-------------corrig´e-------------- SoitC={]a,b],a,b?R,a < b}etT(C) la tribu engendr´ee parC. Comme ]a,b] =∩n>0]a,b+1n on voit que ]a,b]? B(R) pour touta,b?R,a < b. Donc, on aC ? B(R) et doncT(C)? B(R). On montre maintenant l"inclusion inverse, c"est-`a-direB(R)?T(C). SoitI=]a,b[ aveca,b?R, a < b. On peut ´ecrireI=?n≥n0]a,b-1n ], avecn0t.q.1n0< b-a. On en d´eduit queI?T(C).
Puis, comme tout ouvert non vide peut s"´ecrire comme r´eunion d´enombrable d"intervalles ouverts
`a extr´emit´es finies (voir le lemme 2.1 page 20), on obtient que tout ouvert appartient `aT(C). Ceci
permet de conclure queB(R)?T(C) et finalement queB(R) =T(C).4. SoitSun sous ensemble dense deR. Montrer queB(RN) est engendr´ee par la classe des boules
ouvertes (ou bien ferm´ees) telles que les coordonn´ees du centre et le rayon appartiennentS. -------------corrig´e-------------- On reprend le mˆeme raisonnement que dans la premi`ere question en rempla¸cantQNparSN(qui est dense dansRN) etQ?+parS?+={s?S;s >0}(qui est dense dansR?+).Corrig´e 16
SoitEun ensemble etA ? P(E).
1. Montrer queAest une alg`ebre (cf. d´efinition 2.4) si et seulement siAv´erifie les deux propri´et´es
suivantes : (a)E? A,(b)A,B? A ?A\B? A. -------------corrig´e-------------- 289•On suppose queAest une alg`ebre. Il est clair que (a) est v´erifi´ee. Pour montrer (b) il suffit
d"utiliser la stabilit´e par intersection finie et par passage au compl´ementaire, cela donne bien
queA\B=A∩Bc? AsiA,B? A. •On suppose maintenant queAv´erifie (a) et (b).On a alors∅=E\E? A, et donc∅,E? A.
On remarque ensuite que, grˆace `a (b),Ac=E\A?EsiA? A. On a donc la stabilit´e deA par passage au compl´ementaire. Soit maintenantA1,A2? A. On aA1∩A2=A1\Ac2, on en d´eduit queA1∩A2? Apar (b) et la stabilit´e deApar passage au compl´ementaire. Une r´ecurrence surndonne alors queA est stable par intersection finie.Enfin, la stabilit´e deApar union finie d´ecoule de la stabilit´e deApar intersection finie et par
passage au compl´ementaire car (?np=0Ap)c=∩np=0Acp.On a bien montr´e queAest une alg`ebre.
2. Soit (Ai)i?Iune famille d"alg`ebres (surE). Montrer que∩i?IAi={A? P(E);A? Aipour tout
i?I}est encore une alg`ebre. -------------corrig´e--------------On peut montrer que∩i?IAiest une alg`ebre en utilisant diretement la d´efinition d"une alg`ebre.
Onb peut aussi le montrer en utilisant la premi`ere question, ce que nous faisons ici. On montre donc que∩i?IAiv´erifie (a) et (b) : •E? ∩i?IAicarE? Aipour touti?I.quotesdbs_dbs1.pdfusesText_1[PDF] exercices espagnol 4ème pdf
[PDF] exercices estimation ponctuelle avec correction
[PDF] exercices et correction de thermodynamique physique
[PDF] exercices et corriges de probabilite en pdf
[PDF] exercices et corrigés des travaux de fin d'exercice maroc
[PDF] exercices et corrigés sur amortissements provisions
[PDF] exercices et corrigés sur la paie 2016
[PDF] exercices et problèmes corrigés de physique nucleaire pdf
[PDF] exercices et problèmes corrigés de thermodynamique chimique nabih khadija
[PDF] exercices et problèmes de chimie générale
[PDF] exercices et problèmes de cryptographie dunod pdf
[PDF] exercices et problèmes de cryptographie pdf
[PDF] exercices et problèmes de radioactivité
[PDF] exercices et problèmes résolus de recherche opérationnelle tome 1 pdf
