MAT 1600 Exercices sur les nombres complexes
Soient z1z2
Premier exercice
consider the plane (P) of equation: x – y + z + 2 = 0 and the two straight lines (D) and (D') defined by the parametric equations: x t. (D) y t 1 z 2t 1.
Les nombres complexes - Lycée dAdultes
Nov 9 2014 À tout complexe z
Nombres complexes (partie 1)
> z = 3i est un imaginaire pur. > z = 3 est un réel. Définition 4 – Ensemble des imaginaires purs. On note iR l'ensemble des imaginaires
Nombres complexes (partie 1) - Editions Ellipses
> z = 3i est un imaginaire pur. > z = 3 est un réel. Définition 4 – Ensemble des imaginaires purs. On note iR l'ensemble des imaginaires
Chapitre 3 : C1 : Nombres complexes
Définition 3. Soit z un complexe de forme algébrique x + iy. 1 Si z est nombre imaginaire pur alors il peut s'écrire sous la forme z = iy.
NOMBRES COMPLEXES (Partie 2)
Propriétés : Soit z et z ' deux nombres complexes. a) z imaginaire : z z. = 3. 2. +. 1. 2 i. On cherche donc un argument ? de z tel que :.
Nombres complexes
i est un nombre complexe tel que i2 = ?1. a est la partie réelle de z et b est la partie imaginaire et on note a = Re (z) et b = Im(z).
Effectuer des calculs algébriques avec les nombres complexes
z = 2i ?1 n'est ni un réel
Forme trigonométrique dun nombre complexe. Applications Niveau
1. Module et argument. 2. Forme trigonométrique d'un nombre complexe z est un imaginaire pur si et seulement si Re(z)=0.
Searches related to z+1/z 1 imaginaire pur PDF
z1 la solution de partie imaginaire positive et par z2 l’autre solution 2) Déterminer le module et un argument de chacune des solutions z1 et z2 3) Déterminer le module et un argument de ( ) 2 z1 et ( )z2 Dans le plan muni d’un repère orthonormal direct (O u v; ;) on considère les points ABA’ et B’ d’affixes respectives :
Comment montrer que le module de Z est un imaginaire pur ?
Je dois montrer que si le module de z est égale à 1 alors (z+1)/ (z-1) est un imaginaire pur ( avec bien-sûr z 1) Cependant je dois trouver deux autres ( ou plus ) méthodes pour le montrer autre qu'en posant z=a+ib et en remplaçant jusqu'à tomber sur un imaginaire pur. Or je ne sais pas comment calculer ce conjugué...
Comment calculer un imaginaire pur ?
Z (barre) = -Z donc Z = (z+1)/ (z-1) est un imaginaire pur. Posté par larrech 05-09-17 à 22:26
Quelle est la différence entre imaginaire pur et imaginaire imaginaire?
Danger imaginaire Sens : Risque inventé. Imaginaire pur Sens : "Imaginaire pur" désigne, dans le domaine des mathématiques, un nombre complexe dont la partie réelle est nulle.
Qu'est-ce que le carré d'un nombre imaginaire pur?
Le carré d'un nombre imaginaire pur est un nombre réel négatif, et les racines carrées d'un nombre réel négatif sont des imaginaires purs. Au XVI e siècle, les travaux de Cardan et de Bombelli ont montré l'intérêt d'utiliser des racines carrées de nombres négatifs dans les calculs.
Past day
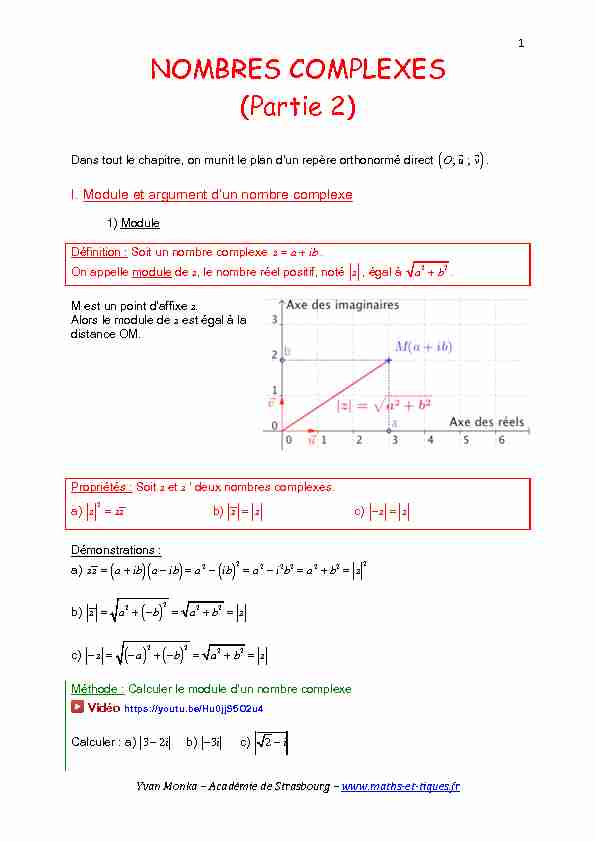
YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr1NOMBRES COMPLEXES (Partie 2) Dans tout le chapitre, on munit le plan d'un repère orthonormé direct
O; u; v . I. Module et argument d'un nombre complexe 1) Module Définition : Soit un nombre complexe z=a+ib . On appelle module de z, le nombre réel positif, noté z , égal à a 2 +b 2. M est un point d'affixe z. Alors le module de z est égal à la distance OM. Propriétés : Soit z et z ' deux nombres complexes. a)
z 2 =zz b) z=z c) -z=zDémonstrations : a)
zz=a+ib a-ib =a 2 -ib 2 =a 2 -i 2 b 2 =a 2 +b 2 =z 2 b) z=a 2 +-b 2 =a 2 +b 2 =z c) -z=-a 2 +-b 2 =a 2 +b 2 =zMéthode : Calculer le module d'un nombre complexe Vidéo https://youtu.be/Hu0jjS5O2u4 Calculer : a) 3-2i
b) -3i c) 2-i YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr2a) 3-2i=3 2 +(-2) 2 =13 b) -3i=-3×i=3×1=3 c) 2-i=2-i=2 2 +-1 2 =2+1=32) Argument Définition : Soit un point M d'affixe z non nulle. On appelle argument de z, noté arg(z) une mesure, en radians, de l'angle
u;OM . Remarques : - Un nombre complexe non nul possède une infinité d'arguments de la forme arg(z)+2kπ k∈! . On notera arg(z) modulo 2π ou arg(z)2π - 0 n'a pas d'argument car dans ce cas l'angle u ;OM n'est pas défini. Exemple : Vidéo https://youtu.be/Hu0jjS5O2u4 Soit z=3+3i . Alors z=3+3i=3 2 +3 2 =18=32 Et arg(z)= 4 2π . Propriétés : Soit z un nombre complexe non nul. a) z est un nombre réel ⇔arg(z)=0π , b) z est un imaginaire pur ⇔arg(z)= 2 . c) arg(z)=-arg(z) d) arg(-z)=arg(z)+πYvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr3Démonstrations : a) Le point M d'affixe z appartient à l'axe des réels. b) Le point M d'affixe z appartient à l'axe des imaginaires. c) d) Ses résultats se déduisent par symétrie. II. Forme trigonométrique d'un nombre complexe 1) Définition Propriété : Soit
z=a+ib un nombre complexe non nul. On pose :θ=arg(z)
On a alors :
a=zcosθ et b=zsinθ . Définition : On appelle forme trigonométrique d'un nombre complexe z non nul l'écriture z=zcosθ+isinθ avecθ=arg(z)
YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr4 Méthode : Ecrire un nombre complexe sous sa forme trigonométrique Vidéo https://youtu.be/zIbpXlgISc4 Ecrire le nombre complexe
z=3+i sous sa forme trigonométrique. - On commence par calculer le module de z : z=3+1=2 - En calculant z z , on peut identifier plus facilement la partie réelle de z et sa partie imaginaire : z z 3 2 1 2 iOn cherche donc un argument θ
de z tel que : cosθ= 3 2 et sinθ= 1 2 . Comme cos 6 3 2 et sin 6 1 2 , on a : z z =cos 6 +isin 6Donc :
z=2cos 6 +isin 6 avec arg(z)= 6 2π. Avec une calculatrice ou un logiciel, il est possible de vérifier les résultats obtenus : 2) Propriétés Inégalité triangulaire : Soit z et z ' deux nombres complexes.
Démonstration : Il s'agit d'une traduction de l'inégalité sur les distances.YvanMonka-AcadémiedeStrasbourg-www.maths-et-tiques.fr5 Propriétés : Soit z et z ' deux nombres complexes non nuls et n entier naturel non nul. Produit
zz'=zz' arg(zz')=arg(z)+arg(z')Puissance
z n =z n arg(z n )=narg(z)Inverse
1 z 1 z arg 1 z =-arg(z)Quotient
z z' z z' arg z z' =arg(z)-arg(z')Démonstration pour le produit : On pose
θ=arg(z)
etθ'=arg(z')
zz'=zcosθ+isinθ z'cosθ'+isinθ' =zz'cosθcosθ'-sinθsinθ' +isinθcosθ'+cosθsinθ' =zz'cosθ+θ' +isinθ+θ'Donc le module de
zz' est zz' et un argument de zz' estθ+θ'=arg(z)+arg(z')
. Horsducadredelaclasse,aucunereproduction,mêmepartielle,autresquecellesprévuesàl'articleL122-5ducodedelapropriétéintellectuelle,nepeutêtrefaitedecesitesansl'autorisationexpressedel'auteur.www.maths-et-tiques.fr/index.php/mentions-legales
quotesdbs_dbs31.pdfusesText_37[PDF] questions ? poser lors dun audit interne
[PDF] questions posées lors dun audit
[PDF] questionnaire audit interne pdf
[PDF] questionnaire d'audit interne gratuit
[PDF] audit interne questionnaire exemple
[PDF] integrale t^n/(1 t)
[PDF] intégrale de exp(-t)ln(t)
[PDF] ln(t)/(1 t^2)
[PDF] intégrale exp(-t)/t
[PDF] integrale sin(t)/t^2
[PDF] integrale sin(t)/t
[PDF] procédés théatraux
[PDF] tendinopathie genou traitement
[PDF] tendinite demi membraneux
