 Feuille de TD no 1 4
Feuille de TD no 1 4
May 25 2022 1. Une chaine de Markov homog`ene de matrice de transition P est. — absorbante si p = 0 ou q = 0. — irréductible non ...
 TD 14 : Convergence de chaînes de Markov Corrigé
TD 14 : Convergence de chaînes de Markov Corrigé
TD 14 : Convergence de chaînes de Markov. Corrigé. Mercredi 20 Décembre. Exercice 1 (Une suite de flips). Soit n ≥ 4. On considère un polygone régulier Pn à n
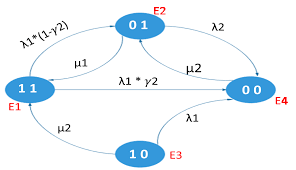 Corrigé dexamen module Sûreté de Fonctionnement (GI 712)
Corrigé dexamen module Sûreté de Fonctionnement (GI 712)
3. Pour une chaine de Markov la durée moyenne d'occupation d'un état peut être définie en quoi: La probabilité d'occuper
 DS: Chaˆınes de Markov: Corrigé succint durée 1h30 Exercice 1. (5
DS: Chaˆınes de Markov: Corrigé succint durée 1h30 Exercice 1. (5
Nov 12 2013 Justifier (en une phrase) que (Xn)n≥0 est une chaıne de Markov homog`ene. Donner son espace d'états et calculer sa matrice de transition P.
 Corrigé type dExamen du module SdF (GI712)
Corrigé type dExamen du module SdF (GI712)
Réponse : Non l'établissement d'une chaine de Markov pour un certain système nécessite non seulement la connaissance des ses composants
 Corrigé de lexamen du 18 avril 2013 (durée 2h)
Corrigé de lexamen du 18 avril 2013 (durée 2h)
Apr 18 2013 a) Pour quelle valeur de α
 Examen : Chaînes de Markov
Examen : Chaînes de Markov
Jan 5 2009 Exercice 1. On considère une chaîne de Markov sur les sommets d'un triangle ABC. Cette chaîne est définie par les règles suivantes : chaque ...
 Corrigé de lexamen du 26 avril 2012 (durée 2h)
Corrigé de lexamen du 26 avril 2012 (durée 2h)
Apr 26 2012 Les trois parties sont indépendantes. Exercice 1 : On considère une chaîne de Markov (Xn)n≥0 sur {1
 Examen de Probabilités: Chaˆınes de Markov 13h30-15h30
Examen de Probabilités: Chaˆınes de Markov 13h30-15h30
Nov 12 2013 Tracer le graphe orienté associé `a P. (Voir annexe). 2. Montrer que la chaıne de Markov est irréductible et apériodique.
 Examen de Probabilités: Chaˆ?nes de Markov 13h30-15h30
Examen de Probabilités: Chaˆ?nes de Markov 13h30-15h30
12 nov. 2013 Tracer le graphe orienté associé `a P. (Voir annexe). 2. Montrer que la cha?ne de Markov est irréductible et apériodique.
 Corrigé de lexamen du 26 avril 2012 (durée 2h)
Corrigé de lexamen du 26 avril 2012 (durée 2h)
26 avr. 2012 Les trois parties sont indépendantes. Exercice 1 : On considère une chaîne de Markov (Xn)n?0 sur {1...
 U.F.R. de Mathématiques Master 2 ISN 2014-2015 Chaînes de
U.F.R. de Mathématiques Master 2 ISN 2014-2015 Chaînes de
Corrigé de l'examen du 4 décembre 2014. Ex 1. [15 points]. Soit (Xn)n?0 la chaîne de Markov homogène à valeurs dans N de matrice de transition.
 U.F.R. de Mathématiques Master 2 ISN 2015-2016 Chaînes de
U.F.R. de Mathématiques Master 2 ISN 2015-2016 Chaînes de
Chaînes de Markov. Corrigé de l'examen du 3 décembre 2015. Les processus de naissance et de mort sont utilisés pour modéliser l'évolution de.
 Corrigé type dExamen du module SdF (GI712)
Corrigé type dExamen du module SdF (GI712)
Est-ce que l'établissement d'une chaine de Markov pour un certain système nécessite uniquement la connaissance de ses composants ? Expliquer.
 Questions de cours Exercices A S B C D
Questions de cours Exercices A S B C D
Examen partiel du 19 novembre 2013. Éléments de correction Donner l'énoncé du théorème ergodique pour les chaînes de Markov récurrentes positives.
 Chaˆ?nes de Markov avancées
Chaˆ?nes de Markov avancées
21 déc. 2012 Corrigé Examen de Chaˆ?nes de Markov. Avancées. Partie I : compréhension du processus et simula- tion. 1.(a) Entre 9h00 et 9h08 ...
 DS: Chaˆ?nes de Markov: Corrigé succint durée 1h30
DS: Chaˆ?nes de Markov: Corrigé succint durée 1h30
12 nov. 2013 Justifier (en une phrase) que (Xn)n?0 est une cha?ne de Markov homog`ene. Donner son espace d'états et calculer sa matrice de transition P.
 Mary - TD 12 – Chaînes de Markov (distributions invariantes) (corrigé)
Mary - TD 12 – Chaînes de Markov (distributions invariantes) (corrigé)
TD 12 – Chaînes de Markov (distributions invariantes) (corrigé). Exercice 1. Proposition utiles. Le but de cet exercice est de démontrer les propriétés
 TD 11 : Chaînes de Markov Corrigé
TD 11 : Chaînes de Markov Corrigé
Corrigé. Mercredi 29 Novembre. 1 Chaînes de Markov. Exercice 1 (Markov ou pas Markov ?) Soit (Sn) une marche aléatoire simple sur Z. Lesquels des processus
 [PDF] Examen de Probabilités: Chaˆ?nes de Markov 13h30-15h30
[PDF] Examen de Probabilités: Chaˆ?nes de Markov 13h30-15h30
12 nov 2013 · Examen de Probabilités: Chaˆ?nes de Markov 13h30-15h30 Exercice 1 (5 points environ) On consid`ere une cha?ne de Markov (Xn)n?0 sur
 [PDF] Processus-M1-2012-Examenpdf
[PDF] Processus-M1-2012-Examenpdf
26 avr 2012 · Corrigé de l'examen du 26 avril 2012 (durée 2h) Exercice 1 : On considère une chaîne de Markov (Xn)n?0 sur {1 7} de matrice de
 [PDF] Examen : Chaînes de Markov
[PDF] Examen : Chaînes de Markov
5 jan 2009 · Exercice 1 On considère une chaîne de Markov sur les sommets d'un triangle ABC Cette chaîne est définie par les règles suivantes : chaque
 [PDF] CHAÎNES DE MARKOV - ceremade
[PDF] CHAÎNES DE MARKOV - ceremade
CHAÎNES DE MARKOV Spécialité : INGENIEUR 1ère année Béatrice de Tilière La partie “Rappels de probabilités” est basée sur des notes écrites en
 [PDF] Chaînes de Markov Corrigé de lexamen du 3 décembre 2015
[PDF] Chaînes de Markov Corrigé de lexamen du 3 décembre 2015
U F R de Mathématiques Master 2 ISN 2015-2016 Chaînes de Markov Corrigé de l'examen du 3 décembre 2015 Les processus de naissance et de mort sont
 [PDF] TD 11 – Chaînes de Markov (récurrence/transience) (corrigé) - CNRS
[PDF] TD 11 – Chaînes de Markov (récurrence/transience) (corrigé) - CNRS
Exercice 2 Chaines de Markov ? Soit (Xn)n?N une chaîne de Markov associée à une matrice de transition P
 [PDF] TD 12 – Chaînes de Markov (distributions invariantes) (corrigé)
[PDF] TD 12 – Chaînes de Markov (distributions invariantes) (corrigé)
TD 12 – Chaînes de Markov (distributions invariantes) (corrigé) Exercice 1 Proposition utiles Le but de cet exercice est de démontrer les propriétés
 [PDF] CORRIGÉ
[PDF] CORRIGÉ
Donner la matrice de transition P de la cha?ne de Markov d'ensemble d'états S = {IMR} modélisant la population `a laquelle appartient cet individu
 [PDF] Examen Chaînes de Markov - Université Paris-Saclay
[PDF] Examen Chaînes de Markov - Université Paris-Saclay
Correction P bien définie car l'irréductibilité implique que l'unique mesure stationnaire est strictement positive en tout point x ; le fait que P soit
 [PDF] TD 7 : Chaînes de Markov - Dimitri Watel
[PDF] TD 7 : Chaînes de Markov - Dimitri Watel
Écrivez la matrice de transition et le graphe associé ? Correction S = 1Pierre Feuille Ciseau Lézard Spockl dans cet ordre
U.F.R. de Mathématiques
Master 2 ISN 2015-2016
Chaînes de MarkovCorrigé de l"examen du 3 décembre 2015 Les processus de naissance et de mort sont utilisés pour modéliser l"évolution de la taille d"une population. Ce sont des chaînes de Markov en temps continu, à valeurs dans l"espace d"étatsN, et telles que les seules transitions possibles à partir d"un état ksoient versk+1(naissance) ou versk-1(mort). Le générateur infinitésimal de ces processus de saut pur est donc de la forme A=( (((((((((((-λ0λ00 0... ... ...1-(λ1+μ1)λ10... ... ...
0μ2-(λ2+μ2)λ20... ......0μ3-(λ3+μ3)λ30.........0............
)))))))))))(1) On admettra qu"un générateur infinitésimal de cette forme est caractéristique d"un processus de naissance et de mort.I. Quelques exemples[10 points]
1)[2 points]Soit(Nt)t≥0un processus de Poisson d"intensitéλ >0. On sait que
(Nt)t≥0est un processus de saut pur, à valeurs entières. Donner une matrice de tran- sitionPet une applicationΛ :N→R?+qui correspondent à ce processus de saut pur. Par construction, lorsque le processus de PoissonNteffectue une transition, c"est pour passer de l"état courant à cet état courant+1. Par ailleurs, le temps entre deux transitions consécutives suit une loi exponentielle de paramètreλ, quel que soit l"état courant. Autrement dit, pour toutn?N,P(n,n+ 1) = 1etΛ(n) =λ.
Commeλ >0, la fonctionΛest bien à valeurs dansR?+.2)[1 point]En déduire le générateur infinitésimal de(Nt)t≥0, puis que ce processus
est bien un processus de naissance et de mort. L"expression du générateur infinitésimal d"un processus de saut pur défini par une matrice de transitionPet une applicationΛest donnée par : A(i,j) = Λ(i)P(i,j)sii?=jetA(i,i) =-Λ(i)(1-P(i,i)). Dans le cas du processus de Poisson, à partir des expressions dePetΛ données ci-dessus, on obtient, pour toutn?N,A(n,n+ 1) =λetA(n,n) =-λ.
Ce générateur infinitésimal est donc bien de la forme caractéristique du générateur infinitésimal d"un processus de naissance et de mort, avecλi=λ, i+1= 0, pour touti≥0. Le processus de Poisson(Nt)t≥0est donc bien un processus de naissance et mort.3)[0,5 point]Quelle est la particularité de ce processus de naissance et de mort?
Comme les seules transitions possibles pour le processus de Poisson sont d"un étatnvers un étatn+ 1, ce processus de naissance et de mort est en fait un processus seulement de naissance.4)[2 points]On souhaite dans ce deuxième exemple modéliser l"évolution d"un
système composé d"appareils indépendants dont les durées de vie suivent une même loi exponentielle de paramètreμ >0. On appelleXtle nombre d"appareils encore en vie à l"instantt, on admet que(Xt)t≥0est une chaîne de Markov en temps continu. Si X0=n≥1, quelle est la loi du premier instant où se produit une transition? Et quelle
est cette transition? Dans le cas oùX0=n≥1, la première transition se produit lorsqu"a lieu la première panne (ou mort) d"un de cesnappareils. Autrement dit, cette première transition se produit auminimumdes temps de vie desnappareils. Chaque appareil ayant une durée de vie de loi exponentielle de paramètre μ, et ces durées de vie étant supposées indépendantes (les appareils le sont), le minimum de cesnvariables aléatoires suit alors une loi exponentielle de paramètrenμ. Enfin, comme la loi commune des durées de vie est à densité, on ne peut avoir plus d"un appareil qui meurt à un instant donné. La transition qui s"effectue est donc de l"étatnvers l"étatn-1.5)[1,5 points]En déduire le générateur infinitésimal de(Xt)t≥0, puis que ce pro-
cessus est bien un processus de naissance et de mort. On peut formaliser ce qui précède en écrivant que la chaîne de Markov (Xt)t≥0est définie par le couple(Λ,P)tel que Λ(n) =nμ, P(n,n-1) = 1sin >0etΛ(0) =c, P(0,0) = 1, oùcest une constante strictement positive quelconque : en effet, comme P(0,0) = 1, peu importe le paramètre de l"exponentielle qui modélise le temps passé en0, puisque quand cette horloge sonne, on reste en0. À partir de là, on en déduit le générateur infinitésimal de ce processus : pourn >0A(n,n-1) =nμetA(n,n) =-nμ,
et tous les autres termes du générateur sont nuls. Il est donc bien de la forme caractéristique d"un processus de naissance et de mort, avec i= 0pour touti?Netμi=iμpour touti≥1. En conclusion, le processus(Xt)t≥0est un processus de naissance et de mort, présentant uniquement des morts. 26)[1,5 points]Dans ce cas particulier, la loi deXtsachant queX0=Nse calcule :
montrer queXtsuit la loi binomiale de paramètresNete-μt. Si l"on travaille conditionnellement àX0=N, alors pour toutt >0, le nombre d"appareils encore en vie à l"instantt,Xt, peut prendre les valeurs0,1,...,N. Pourk? {0,1,...,N},{Xt=k}signifie quekappareils sont
encore en vie à l"instantt, etN-ksont morts avant l"instantt. La proba- bilité d"être encore en vie à l"instanttest lamêmepour tous les appareils : c"este-μt, puisque la durée de vie des appareils suit la loi exponentielle de paramètreμ. Enfin, les appareils sont indépendants, donc il y a indépen- dance des évènements " l"appareiliest encore en vie à l"instantt», pouri variant entre1etN.Au total, pourk? {0,1,...,N},
P(Xt=k|X0=N) =CkN(e-μt)k(1-e-μt)N-k,
la loi deXtsachantX0=Nest donc la loi binomiale de paramètre(N,e-μt).7)[1,5 points]Soit maintenant(Xt)t≥0une file d"attente M/M/1,λ >0étant
le paramètre de la loi exponentielle des inter-arrivées,μ >0le paramètre de la loi exponentielle des temps de service. Rappeler ce que vaut le générateur infinitésimal dans ce cas, et en déduire que la file d"attente(Xt)t≥0est un processus de naissance et mort. Le générateur infinitésimal d"une telle file d"attente est donné par A=( (((((((((((-λ λ0 0... ... ...μ-(λ+μ)λ0... ... ...
0μ-(λ+μ)λ0... ......0μ-(λ+μ)λ0.........0............
Sa forme correspond donc à celle, caractéristique, du générateur d"un pro- cessus de naissance et mort, avecλi=λetμi+1=μpour touti≥0: les files d"attente M/M/1 sont des processus de naissance et mort.II. Comportement en temps long[7 points]
On s"intéresse dans cette partie au comportement en temps long des processus de naissance et de mort, et en particulier à l"existence d"un régime stationnaire, qui correspond à l"existence d"une probabilité surN,π, qui est invariante pour ce processus. Cette invariance se caractérise par l"équationπA= 0,
oùAest le générateur infinitésimal du processus donné par l"équation (1). 38)[1 point]Écrire les équations de récurrence vérifiées parπ.
La première colonne de la matriceAest la seule qui est différente de toutes les autres. Ceci conduit aux deux " équations » suivantes : -λ0π0+μ1π1= 0etλnπn-(λn+1+μn+1)πn+1+μn+2πn+2= 0?n≥0.9)[1 point]Montrer qu"elles sont équivalentes au système d"équationsμnπn=
n-1πn-1pour toutn≥1. Ce système infini d"équations se réécrit Il est alors immédiat que la première équation permet d"initialiser la récur- rence, et que les autres équations entraînent l"hérédité de la propriété. On a donc finalement l"équivalence avec le système infini d"équations suivant : n+1πn+1=λnπn?n≥0.10)[1,5 points]En déduire l"expression deπnen fonction deπ0, pour toutn≥1,
puis une condition nécessaire et suffisante d"existence de la probabilité invarianteπ. On suppose ici queμn>0pour toutn≥1. Les équations ci-dessus se réécrivent alorsπn+1=λnμ n+1πnpour toutn≥0, ce qui conduit finalement n=λn-1λn-2···λ0μ nμn-1···μ1π0?n≥1.
Il existe alors une probabilité invariante si et seulement si la série desπn converge, autrement dit si et seulement si n=1λ n-1λn-2···λ0μ nμn-1···μ1<+∞.(2)11)[0,5 points]Dans le cas où cette probabilité invariante existe, donner l"expression
deπ0. On suppose que la convergence (2) a lieu. On détermine alorsπ0viala condition de normalisation? n≥0πn= 1. Celle-ci s"écrit dans notre cas 1 = n≥0π n=π0++∞? n=1λ n-1λn-2···λ0μ nμn-1···μ1π0=π0?
1 ++∞?
n=1λ n-1λn-2···λ0μ nμn-1···μ1? d"oùπ0=?1 ++∞?
n=1λ n-1λn-2···λ0μ nμn-1···μ1? -112)[1 point]Dans le cas particulier des files d"attente M/M/1 étudié Question 7, ré-
écrire la condition d"existence d"une probabilité invariante, et en déduire une condition s"exprimant simplement en fonction deλetμ. Dans le cas des files d"attente M/M/1, on aλn=λetμn+1=μpour tout n≥0. La condition d"existence d"une probabilité invariante (2) se réécrit alors?+∞n=1(λ/μ)n<+∞, et comme on reconnaît une sériegéométrique, on sait que la convergence a lieu si et seulement si|λ/μ|<1, autrement dit si et seulement siλ < μ, puisque ces quantités sont positives. 413)[1 point]Dans ce cas, donner la probabilité invariante associée à la file d"attente.
On suppose queλ < μ. On aπn= (λ/μ)nπ0pour toutn≥0, et 0=?1 ++∞?
n=1? n?-1 n=0? n?-1 =?11-λ/μ?quotesdbs_dbs4.pdfusesText_7[PDF] temperature pdf
[PDF] la chambre des officiers résumé film
[PDF] la chambre des officiers questionnaire reponse
[PDF] la chambre des officiers contexte historique
[PDF] la chambre des officiers clemence
[PDF] procédure de délogement d'un client
[PDF] comment satisfaire un client ayant été délogé subitement
[PDF] délogement interne ou externe
[PDF] overbooking hotel definition
[PDF] lancement d'une entreprise module 1
[PDF] lancement d'une entreprise module 7
[PDF] lancement d une entreprise module 4
[PDF] présenter une entreprise dans un mémoire
[PDF] exemple de présentation d'entreprise pour rapport de stage
