 Feuille de TD no 1 4
Feuille de TD no 1 4
May 25 2022 1. Une chaine de Markov homog`ene de matrice de transition P est. — absorbante si p = 0 ou q = 0. — irréductible non ...
 TD 14 : Convergence de chaînes de Markov Corrigé
TD 14 : Convergence de chaînes de Markov Corrigé
TD 14 : Convergence de chaînes de Markov. Corrigé. Mercredi 20 Décembre. Exercice 1 (Une suite de flips). Soit n ≥ 4. On considère un polygone régulier Pn à n
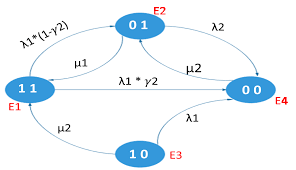 Corrigé dexamen module Sûreté de Fonctionnement (GI 712)
Corrigé dexamen module Sûreté de Fonctionnement (GI 712)
3. Pour une chaine de Markov la durée moyenne d'occupation d'un état peut être définie en quoi: La probabilité d'occuper
 U.F.R. de Mathématiques Master 2 ISN 2015-2016 Chaînes de
U.F.R. de Mathématiques Master 2 ISN 2015-2016 Chaînes de
Chaînes de Markov. Corrigé de l'examen du 3 décembre 2015. Les processus de naissance et de mort sont utilisés pour modéliser l'évolution de la taille d'une
 DS: Chaˆınes de Markov: Corrigé succint durée 1h30 Exercice 1. (5
DS: Chaˆınes de Markov: Corrigé succint durée 1h30 Exercice 1. (5
Nov 12 2013 Justifier (en une phrase) que (Xn)n≥0 est une chaıne de Markov homog`ene. Donner son espace d'états et calculer sa matrice de transition P.
 Corrigé type dExamen du module SdF (GI712)
Corrigé type dExamen du module SdF (GI712)
Réponse : Non l'établissement d'une chaine de Markov pour un certain système nécessite non seulement la connaissance des ses composants
 Corrigé de lexamen du 18 avril 2013 (durée 2h)
Corrigé de lexamen du 18 avril 2013 (durée 2h)
Apr 18 2013 a) Pour quelle valeur de α
 Examen : Chaînes de Markov
Examen : Chaînes de Markov
Jan 5 2009 Exercice 1. On considère une chaîne de Markov sur les sommets d'un triangle ABC. Cette chaîne est définie par les règles suivantes : chaque ...
 Corrigé de lexamen du 26 avril 2012 (durée 2h)
Corrigé de lexamen du 26 avril 2012 (durée 2h)
Apr 26 2012 Les trois parties sont indépendantes. Exercice 1 : On considère une chaîne de Markov (Xn)n≥0 sur {1
 Examen de Probabilités: Chaˆınes de Markov 13h30-15h30
Examen de Probabilités: Chaˆınes de Markov 13h30-15h30
Nov 12 2013 Tracer le graphe orienté associé `a P. (Voir annexe). 2. Montrer que la chaıne de Markov est irréductible et apériodique.
 Examen de Probabilités: Chaˆ?nes de Markov 13h30-15h30
Examen de Probabilités: Chaˆ?nes de Markov 13h30-15h30
12 nov. 2013 Tracer le graphe orienté associé `a P. (Voir annexe). 2. Montrer que la cha?ne de Markov est irréductible et apériodique.
 Corrigé de lexamen du 26 avril 2012 (durée 2h)
Corrigé de lexamen du 26 avril 2012 (durée 2h)
26 avr. 2012 Les trois parties sont indépendantes. Exercice 1 : On considère une chaîne de Markov (Xn)n?0 sur {1...
 U.F.R. de Mathématiques Master 2 ISN 2014-2015 Chaînes de
U.F.R. de Mathématiques Master 2 ISN 2014-2015 Chaînes de
Corrigé de l'examen du 4 décembre 2014. Ex 1. [15 points]. Soit (Xn)n?0 la chaîne de Markov homogène à valeurs dans N de matrice de transition.
 U.F.R. de Mathématiques Master 2 ISN 2015-2016 Chaînes de
U.F.R. de Mathématiques Master 2 ISN 2015-2016 Chaînes de
Chaînes de Markov. Corrigé de l'examen du 3 décembre 2015. Les processus de naissance et de mort sont utilisés pour modéliser l'évolution de.
 Corrigé type dExamen du module SdF (GI712)
Corrigé type dExamen du module SdF (GI712)
Est-ce que l'établissement d'une chaine de Markov pour un certain système nécessite uniquement la connaissance de ses composants ? Expliquer.
 Questions de cours Exercices A S B C D
Questions de cours Exercices A S B C D
Examen partiel du 19 novembre 2013. Éléments de correction Donner l'énoncé du théorème ergodique pour les chaînes de Markov récurrentes positives.
 Chaˆ?nes de Markov avancées
Chaˆ?nes de Markov avancées
21 déc. 2012 Corrigé Examen de Chaˆ?nes de Markov. Avancées. Partie I : compréhension du processus et simula- tion. 1.(a) Entre 9h00 et 9h08 ...
 DS: Chaˆ?nes de Markov: Corrigé succint durée 1h30
DS: Chaˆ?nes de Markov: Corrigé succint durée 1h30
12 nov. 2013 Justifier (en une phrase) que (Xn)n?0 est une cha?ne de Markov homog`ene. Donner son espace d'états et calculer sa matrice de transition P.
 Mary - TD 12 – Chaînes de Markov (distributions invariantes) (corrigé)
Mary - TD 12 – Chaînes de Markov (distributions invariantes) (corrigé)
TD 12 – Chaînes de Markov (distributions invariantes) (corrigé). Exercice 1. Proposition utiles. Le but de cet exercice est de démontrer les propriétés
 TD 11 : Chaînes de Markov Corrigé
TD 11 : Chaînes de Markov Corrigé
Corrigé. Mercredi 29 Novembre. 1 Chaînes de Markov. Exercice 1 (Markov ou pas Markov ?) Soit (Sn) une marche aléatoire simple sur Z. Lesquels des processus
 [PDF] Examen de Probabilités: Chaˆ?nes de Markov 13h30-15h30
[PDF] Examen de Probabilités: Chaˆ?nes de Markov 13h30-15h30
12 nov 2013 · Examen de Probabilités: Chaˆ?nes de Markov 13h30-15h30 Exercice 1 (5 points environ) On consid`ere une cha?ne de Markov (Xn)n?0 sur
 [PDF] Processus-M1-2012-Examenpdf
[PDF] Processus-M1-2012-Examenpdf
26 avr 2012 · Corrigé de l'examen du 26 avril 2012 (durée 2h) Exercice 1 : On considère une chaîne de Markov (Xn)n?0 sur {1 7} de matrice de
 [PDF] Examen : Chaînes de Markov
[PDF] Examen : Chaînes de Markov
5 jan 2009 · Exercice 1 On considère une chaîne de Markov sur les sommets d'un triangle ABC Cette chaîne est définie par les règles suivantes : chaque
 [PDF] CHAÎNES DE MARKOV - ceremade
[PDF] CHAÎNES DE MARKOV - ceremade
CHAÎNES DE MARKOV Spécialité : INGENIEUR 1ère année Béatrice de Tilière La partie “Rappels de probabilités” est basée sur des notes écrites en
 [PDF] Chaînes de Markov Corrigé de lexamen du 3 décembre 2015
[PDF] Chaînes de Markov Corrigé de lexamen du 3 décembre 2015
U F R de Mathématiques Master 2 ISN 2015-2016 Chaînes de Markov Corrigé de l'examen du 3 décembre 2015 Les processus de naissance et de mort sont
 [PDF] TD 11 – Chaînes de Markov (récurrence/transience) (corrigé) - CNRS
[PDF] TD 11 – Chaînes de Markov (récurrence/transience) (corrigé) - CNRS
Exercice 2 Chaines de Markov ? Soit (Xn)n?N une chaîne de Markov associée à une matrice de transition P
 [PDF] TD 12 – Chaînes de Markov (distributions invariantes) (corrigé)
[PDF] TD 12 – Chaînes de Markov (distributions invariantes) (corrigé)
TD 12 – Chaînes de Markov (distributions invariantes) (corrigé) Exercice 1 Proposition utiles Le but de cet exercice est de démontrer les propriétés
 [PDF] CORRIGÉ
[PDF] CORRIGÉ
Donner la matrice de transition P de la cha?ne de Markov d'ensemble d'états S = {IMR} modélisant la population `a laquelle appartient cet individu
 [PDF] Examen Chaînes de Markov - Université Paris-Saclay
[PDF] Examen Chaînes de Markov - Université Paris-Saclay
Correction P bien définie car l'irréductibilité implique que l'unique mesure stationnaire est strictement positive en tout point x ; le fait que P soit
 [PDF] TD 7 : Chaînes de Markov - Dimitri Watel
[PDF] TD 7 : Chaînes de Markov - Dimitri Watel
Écrivez la matrice de transition et le graphe associé ? Correction S = 1Pierre Feuille Ciseau Lézard Spockl dans cet ordre
Cha^nes de Markov avancees
M2 Genie Biologique et Informatique { Premier semestre 2012{2013Mikael Falconnet mikael.falconnet@genopole.cnrs.frTable des matieres1 Processus de Poisson 2
1.1 Rappels sur la loi exponentielle . . . . . . . . . . . . . . . . . .
21.2 Processus de Poisson : denition et propriete principale . . .
51.3 Processus de Poisson et loi exponentielle . . . . . . . . . . . .
71.4 Proprietes supplementaires . . . . . . . . . . . . . . . . . . . . .
92 Modeles d'evolution de sequences biologiques 10
2.1 Modeles markoviens de substitution de nucleotides . . . . . .
102.2 Distance phylogenetique . . . . . . . . . . . . . . . . . . . . . .
172.3 Modeles Markoviens de substitution de codons . . . . . . . . .
20A Correction des exercices 22
B Sujets d'examen 49
B.1 Premiere Session 2012{2013 . . . . . . . . . . . . . . . . . . . . 49B.2 Seconde Session 2012{2013 . . . . . . . . . . . . . . . . . . . . . 62
1 L'objectif de ce cours est de familiariser les etudiants avec les cha^nes de Markov a temps continu et en particulier a la modelisation de l'evolution de sequences biologiques. On introduira la loi exponentielle et les processus de Poisson, la notion de generateur innitesimal sera abordee a travers les modeles markoviens de substitutions de nucleotides et nous evoquerons egalement les modeles de substitution de codons. La simulation sous le logicielRoccupera une part importante du module.
1 Processus de Poisson
1.1 Rappels sur la loi exponentielle
La loi exponentielle joue un r^ole fondamental dans les processus de Poisson et les cha^nes de Markov a temps continu. Nous en exposons ici les proprietes principales.Denition 1.1
(loi exponentielle).La loi exponentielle de parametre¸, (avec¸È0), noteeExp(¸)est la loi de densite
x7!¸e¡¸x,x>0. En particulier,Csuit une loi exponentielle de parametre¸si et seulement siP(CÈt)AEe¡¸t,pour toutt>0.
La notationCest un choix personnel et provient de la premiere lettre declock signianthorlogeen anglais. En eet, dans la majorite des situations rencon- trees, les variables aleatoires suivant des lois exponentielles representeront des temps d'attente entre deux arrivees. On peut donc se representerCcomme le temps de sonnerie d'une horloge aleatoire suivant une loi exponentielle. La notationTsera reservee aux temps d'arrivee. Proposition 1.2.La loi exponentielle satisfait les proprietes suivantes. (i)P(CÈtÅujCÈu)AEP(CÈt)AEe¡¸t, pour toust,uÈ0. (ii)P(C6tÅsjCÈt)AE¸s[1Å"(s)], ou"(s)!0quands!0. (iii) SoientC1,C2,...,Cndes variables aleatoires independantes distribuees suivant des lois exponentielles de parametres¸1,¸2,...,¸n. AlorsCAEmin(C1,...,Cn)suit une loi exponentielle de parametrePn iAE1¸i. La propriete(i), appeleeabsence de memoire, caracterise la loi exponentielle, c'est a dire que c'est la seule loi continue qui possede cette propriete. La demonstration est un elegant exercice sur les equations fonctionnelles. Plus 2 important est l'interpretation de(i). Elle signie que si l'horloge n'a pas sonne jusqu'au tempsu, la probabilite qu'elle sonne dans l'intervalle(u,tÅu] ne depend que detet pas deu. L'horloge a "oublie" qu'elle n'avait pas sonne jusqu'au tempsuet s'est reinitialisee. Cette propriete peut sembler perturbante quand on pense queCpeut representer le temps de panne d'une machine. En eet, l'absence de memoire dans ce cas revient a oublier l'usure de la machine. Le propriete(ii)signie que si une horloge suit une loi exponentielle de parametre¸, la probabilite qu'elle sonne dans un petit intervalle de longueur sest approximativement¸s. La propriete(iii)signie que si je regardenhorloges independantes alors le temps d'attente de la premiere sonnerie parmi cesnhorloges est aussi une loi exponentielle. Preuve de la proposition 1.2.Montrons(i). Nous avons¡¸uAEe¡¸t.
Montrons(ii). Nous avons
Montrons(iii). Nous avons par denition deC
P(CÈt)AEP(C1Èt,...CnÈt),
puis gr^ace a l'independance des variables aleatoiresC1,C2,...,CnP(CÈt)AEnY
iAE1P(CiÈt)AEnY iAE1e¡¸itAEe¡tPn iAE1¸i.Exercice I(Illustration de la propriete (iii) de la proposition 1.2). 1. Rappeler la fonction de densite d'une loi exponentielle de parametre ¸AE2et tracer sa courbe a l'aide deR. On pourra utiliser les fonctions plotetdexp. 2. Simuler unn-echantillon d'une loi exponentielle de parametre¹È0 avecnAE500et¹AE1. On pourra utiliser la fonctionrexp. 3. Simuler unn-echantillon du minimum de deux lois exponentielles independantes de parametres¹1AE¹2AE1avecnAE500. On pourra utiliser la fonctionpmin. 4. Tracer l'histogramme d'unn-echantillon du minimum de deux exponen- tielles independantes de parametre¹1AE¹2AE1, avecnAE500. On pourra utiliser la fonctionhist. 35.Tracer sur le m^eme graphique la fonction de densite d'une loi expo-
nentielle de parametre¸AE2et l'histogramme d'unn-echantillon du minimum de deux exponentielles independantes de parametre¹1AE¹2AE1 avecnAE500. On pourra utiliser l'optionbreaksdans la fonctionhist pour aner l'histogramme. 6.R eprendrel aq uestion4. a vecnAE1000.
7. ^Etes-vous convaincu quant a la propriete (iii) de la proposition 1.2? Plut^ot que d'utiliser un histogramme pour representer unn-echantillon et se demander si il correspond a la \bonne" loi de densite, nous allons utiliser un autre outil : la fonction de repartition empirique.Denition.
SoitXune variable aleatoire reelle. La fonction de repartitionF deXest donnee parF(x)AEP(X6x).
Denition.
En statistique, la fonction de repartition empiriqueFn(¢)d'un n-echantillonX1,...,Xnest une fonction aleatoire en escalier denie par F n(x)AEnombre d'elements6xdans l'echantillonn AE1n n X iAE11{Xi6x}.Theoreme
(Theoreme de Glivenko-Cantelli).SoitX1,...,Xnunn-echantillon ou chaqueXia pour fonction de repartitionF. Alors presque s^urement, la fonction de repartition empiriqueFn(¢)converge uniformement versFquandn tend vers l'inni.Exercice II
(Une meilleure illustration de la propriete (iii) de la proposi- tion 1.2). 1. On suppose queX1AE2,X2AE1,X3AE2.5etX4AE3.5. Tracer a la main puis a l'aide deRla fonction de repartition empirique de cet echantillon. On pourra utiliser la fonctionecdf. Dans un souci esthetique, on utilisera les optionsverticals=TRUEetdo.points=FALSE. 2. Donner la fonction de repartition d'une loi exponentielle de parametre¸AE2et tracer sa courbe a l'aide deR.
3. Tracer sur le m^eme graphique la fonction de repartition d'une loi exponentielle de parametre¸AE2et la fonction de repartition empirique d'unn-echantillon du minimum de deux exponentielles independantes de parametre¹1AE¹2AE1avecnAE500. 4.R eprendrel aq uestion3. a vecnAE1000.
5. ^Etes-vous convaincu quant a la propriete (iii) de la proposition 1.2? 41.2 Processus de Poisson : denition et propriete principaleParmi les processus stochastiques a temps continu, le processus de Poisson
occupe une place privilegiee. Il est utilise pour decrire la realisation dans le temps d'evenements aleatoires d'un type donne. Classiquement, on retrouve l'arrivee de clients a un guichet, l'arrivee de demandes de t^aches sur une im- primante, l'occurrence d'accidents dans une entreprise, etc. Schematiquement, ceci revient a modeliser les temps de sonnerie d'une horloge aleatoire.Denition 1.3
(Processus de comptage).La description mathematique d'un ux d'evenements aleatoires peut se faire de deux manieres dierentes. 1. O nc onsiderel enom bred' evenementsN(t)se produisant dans l'inter- valle de temps[0,t]et on cherche a determiner la distribution de cette variable aleatoire discrete. Le processus stochastique{N(t) :t>0}est appeleprocessus de comptage, ses realisations sont des fonctions en escalier croissantes (gure 1). Notons queN(uÅt)¡N(u)indique le nombre aleatoire d'evenements se produisant dans l'intervalle]u,tÅu].2.On considere les intervalles de temps qui separent les instants d'appa-
rition de deux evenements consecutifs. Ce sont des variables aleatoires continues et positives dont on admettra generalement qu'elles sont independantes et identiquement distribuees. La connaissance de leur distribution commune permettra alors de determiner les proprietes du processus de comptage correspondant. Soit{N(t) :t>0}un processus de comptage et designons parCnla duree separant le(n¡1)-ieme evenement dun-ieme pourn>1. La variable aleatoire Cn, appeletemps d'attente, represente le temps pendant lequel le processus demeure dans l'etatn¡1. Posons ensuite T nAEC1ÅC2Å¢¢¢ÅCn, qui est le temps ecoule jusqu'a la realisation dun-ieme evenement. On verie aisement queDenition 1.4
(Processus de Poisson).On dit qu'un processus de comptage {N(t) :t>0}est unprocessus de Poissons'il satisfait aux quatre conditions suivantes. (H1) Le processusN(t)est homogene dans le temps. Ceci veut dire que la probabilite d'avoirkevenements dans un intervalle de longueur donnee 5N(t)012345
tT 1T 2T 3T 4T 5C 1Cquotesdbs_dbs4.pdfusesText_7[PDF] temperature pdf
[PDF] la chambre des officiers résumé film
[PDF] la chambre des officiers questionnaire reponse
[PDF] la chambre des officiers contexte historique
[PDF] la chambre des officiers clemence
[PDF] procédure de délogement d'un client
[PDF] comment satisfaire un client ayant été délogé subitement
[PDF] délogement interne ou externe
[PDF] overbooking hotel definition
[PDF] lancement d'une entreprise module 1
[PDF] lancement d'une entreprise module 7
[PDF] lancement d une entreprise module 4
[PDF] présenter une entreprise dans un mémoire
[PDF] exemple de présentation d'entreprise pour rapport de stage
