 1.3 Les méthodes directes
1.3 Les méthodes directes
1.3.2 Méthode de Gauss méthode LU. Soit A ∈ Mn(IR) une matrice inversible La factorisation LU de la matrice découle immédiatement de l'algorithme de Gauss.
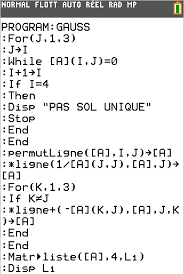 Algorithme de la résolution par le pivot de Gauss dun système 3x3
Algorithme de la résolution par le pivot de Gauss dun système 3x3
20 oct. 2015 Algorithme de la résolution par le pivot de Gauss d'un système 3x3. 1 La méthode. 1.1 Un exemple. Le but est d'éliminer successivement l ...
 Cours 1: Autour des systèmes linéaires Algorithme du pivot de
Cours 1: Autour des systèmes linéaires Algorithme du pivot de
Une méthode pour inverser une matrice : Pivot de Gauss. L'algorithme général. Remarque importante. Il existe des applications qui n'admettent pas d'inverse
 1 Méthode de Gauss et factorisation LU
1 Méthode de Gauss et factorisation LU
(c) Résoudre le système (1) par l'algorithme de Gauss avec pivot partiel. (d) Calculer la factorisation ¯L¯U de PA (où P est la matrice produit des matrices de
 Cours 1: Autour des systèmes linéaires Algorithme du pivot de Gauss
Cours 1: Autour des systèmes linéaires Algorithme du pivot de Gauss
Methode plus "automatique" : le pivot de Gauss sur les sytémes linéaires. But de l'algorithme. Opérations autorisées. Un exemple avant la "théorie". Mécanismes
 S54MA2M7 : Informatique 2 Le pivot de Gauss et al.
S54MA2M7 : Informatique 2 Le pivot de Gauss et al.
5 mars 2019 ▷ A est triangulaire supérieure. Avec l'algorithme de solution des systèmes triangulaires donne une méthode pour résoudre (A
 Résolution des syst`emes linéaires Méthode de Gauss
Résolution des syst`emes linéaires Méthode de Gauss
Cet algorithme permet ainsi de calculer rapi- dement
 Analyse Numérique
Analyse Numérique
L'algorithme de Gauss Si A est une matrice symétrique définie positive alors la méthode de Gauss-. Seidel converge (la méthode de Jacobi pas forcément).
 Informatique en CPGE (2018-2019) Résolution dun système
Informatique en CPGE (2018-2019) Résolution dun système
méthode de Gauss. S. B.. Lycée des EK. 12 mars 2019. S. B. Le principe de l'algorithme du pivot de Gauss est d'exécuter des tâches répétitives qui ...
 Algorithme du Pivot de Gauss
Algorithme du Pivot de Gauss
Le but de ce cours est l'étude de la résolution de systèmes linéaires. Nous nous intéresserons tout particulièrement à la méthode du pivot de Gauss déjà
 Algorithme de la résolution par le pivot de Gauss dun système 3x3
Algorithme de la résolution par le pivot de Gauss dun système 3x3
20 oct. 2015 Algorithme de la résolution par le pivot de Gauss d'un système 3x3. 1 La méthode. 1.1 Un exemple. Le but est d'éliminer successivement ...
 Résolution des syst`emes linéaires Méthode de Gauss
Résolution des syst`emes linéaires Méthode de Gauss
Méthode de Gauss. Méthodes numériques 2003/2004 - D.Pastre licence de mathématiques et licence MASS Cet algorithme permet ainsi de calculer rapi-.
 Étape A : processus délimination de Gauss
Étape A : processus délimination de Gauss
Dans chaque cas on écrira les étapes de la méthode sous forme matricielle. 2. (algo) Soit M ? Mn(R) une matrice carrée inversible et soit b ? Rn un
 Cours 1: Autour des systèmes linéaires Algorithme du pivot de Gauss
Cours 1: Autour des systèmes linéaires Algorithme du pivot de Gauss
Methode plus "automatique" : le pivot de Gauss sur les sytémes linéaires. Cours 1: Autour des systèmes linéaires. Algorithme du pivot de Gauss. Clément Rau.
 Informatique en CPGE (2018-2019) Résolution dun système
Informatique en CPGE (2018-2019) Résolution dun système
12 mars 2019 Algorithme du pivot de Gauss. Utilisation de NumPy. Informatique en CPGE (2018-2019). Résolution d'un système linéaire inversible: méthode ...
 Cours 4 : Gauss et LU
Cours 4 : Gauss et LU
par des méthodes directes : Gauss LU
 Méthode du pivot de Gauss
Méthode du pivot de Gauss
Méthode du pivot de Gauss. On veut écrire un algorithme qui: 1. Renvoie l'unique solution de AX = B si A est inversible.
 Cours 1: Autour des systèmes linéaires Algorithme du pivot de
Cours 1: Autour des systèmes linéaires Algorithme du pivot de
Methode plus "automatique" : le pivot de Gauss sur les sytémes linéaires. Introduction aux matrices. Cours 1: Autour des systèmes linéaires. Algorithme du
 S54MA2M7 : Informatique 2 Le pivot de Gauss et al.
S54MA2M7 : Informatique 2 Le pivot de Gauss et al.
5 mars 2019 ? A est triangulaire supérieure. Avec l'algorithme de solution des systèmes triangulaires donne une méthode pour résoudre (A
 [PDF] Méthode du pivot de Gauss
[PDF] Méthode du pivot de Gauss
La méthode du pivot permet d'associer `a tout syst`eme linéaire un syst`eme facile équivalent Elle consiste `a sélectionner une équation qu'on va garder
 [PDF] Algorithme du Pivot de Gauss - CPGE du Lycée Montesquieu
[PDF] Algorithme du Pivot de Gauss - CPGE du Lycée Montesquieu
Le but de ce cours est l'étude de la résolution de systèmes linéaires Nous nous intéresserons tout particulièrement à la méthode du pivot de Gauss déjà
 [PDF] Résolution des syst`emes linéaires Méthode de Gauss - Normale Sup
[PDF] Résolution des syst`emes linéaires Méthode de Gauss - Normale Sup
Méthode de Gauss Méthodes numériques 2003/2004 - D Pastre licence de mathématiques et licence MASS Cet algorithme permet ainsi de calculer rapi-
 [PDF] Chapitre V La méthode du pivot de Gauss et ses applications
[PDF] Chapitre V La méthode du pivot de Gauss et ses applications
- Intervertir deux équations : - Intervertir l'ordre des inconnues - Remplacer une équation par La technique du pivot : On décrit l'algorithme qui permet
 [PDF] METHODE DU PIVOT DE GAUSS - Toutes les Maths
[PDF] METHODE DU PIVOT DE GAUSS - Toutes les Maths
METHODE DU PIVOT DE GAUSS La méthode du pivot de Gauss permet la résolution générale des systèmes d'équations linéaires à n équations et p inconnues
 [PDF] Cours 1: Autour des systèmes linéaires Algorithme du pivot de Gauss
[PDF] Cours 1: Autour des systèmes linéaires Algorithme du pivot de Gauss
Méthode par substitution Méthode par addition 3 Methode plus "automatique" : le pivot de Gauss sur les sytémes linéaires But de l'algorithme
 [PDF] Algorithme de la résolution par le pivot de Gauss dun système 3x3
[PDF] Algorithme de la résolution par le pivot de Gauss dun système 3x3
20 oct 2015 · Algorithme de la résolution par le pivot de Gauss d'un système 3x3 1 La méthode 1 1 Un exemple Le but est d'éliminer successivement
 [PDF] Chapitre 2 Résolution des Systèmes Linéaires Ax=b Méthodes
[PDF] Chapitre 2 Résolution des Systèmes Linéaires Ax=b Méthodes
Soit un système linéaire Ax = b l'algorithme de Gauss sans pivotation est la méthode classique de substitution La matrice d'origine A est d'abord
 [PDF] 13 Les méthodes directes
[PDF] 13 Les méthodes directes
La factorisation LU de la matrice découle immédiatement de l'algorithme de Gauss Voyons comment sur l'exem- ple précédent
 [PDF] XI Algorithme de Gauss-Jordan - Emmanuel Morand
[PDF] XI Algorithme de Gauss-Jordan - Emmanuel Morand
Algorithme de Gauss-Jordan 1 Opérations élémentaires sur les lignes d'une matrice Définition 1 On définit trois types d'opérations élémentaires sur les
Comment faire la méthode de Gauss ?
La méthode du pivot de Gauss est une méthode pour transformer un système en un autre système équivalent (ayant les mêmes solutions) qui est triangulaire et est donc facile à résoudre. Les opérations autorisées pour transformer ce système sont : échange de deux lignes. multiplication d'une ligne par un nombre non nul.Quelle est la formule du pivot de Gauss ?
La méthode du pivot permet d'associer `a tout syst`eme linéaire un syst`eme facile équivalent. ? 2x + 3y + z = 1 ?7y + 7z = 1 ?7y ? 3z = ?2. on résout le syst`eme dérivé (par combinaison linéaire) et on conclut avec l'équation facile.Qu'est-ce qu'un pivot maths ?
Définition - Une matrice est échelonnée si le nombre de 0 au début de chaque ligne est strictement croissant quand on passe d'une ligne à la suivante. Le premier élément non nul de chaque ligne dans une matrice échelonnée s'appelle le pivot.- La transformation de Gauss-Jordan consiste à transformer ce système en un système équivalent dont le bloc gauche est l'identité, c'est-à-dire qu'il faut modifier la matrice (A I) pour qu'elle devienne de la forme (I A ? 1) en utilisant les propriétés de l'algorithme.
Exercice 5
1. Résoudre le système linéaireAx=bpar la méthode d"élimination de Gauss dans les trois cas suivants :
a- A=242 4 6
2 1 1 11 23 5 b=2 441 53
5 b- A=2
42 4 6
24 111 23 5 b=2 412
5 03 5 c- A=2
42 4 6
24 112 23 5 b=2 412
5 13 5 oub=2 42
2 43
5 Dans chaque cas, on écrira les étapes de la méthode sous forme matricielle.
2.(algo)SoitM2 Mn(R)une matrice carrée inversible et soitb2Rnun vecteur (b2 Mn;1(R)). Écrire l"algorithme
d"élimination de Gauss pour résoudre le système linéaireMx=b.Question 1a.Étape A : processus d"élimination de Gauss
On transforme le systèmeAx=ben un système triangulaire supérieurUx=~boùUest une matrice triangulaire supérieure
à diagonale unité en faisant des combinaisons linéaires des équations (ce qui équivaut à faire des combinaisons linéaires des
lignes deA).Étape A1 :
On éliminex1dans les équations2et3(en faisant une combinaison linéaire entre la première et la deuxième équations d"une
part, et entre la première et la troisième équations d"autre part) : L2 L2+L1etL3 L3+12
L1:(1)
On obtient le système
A1x=b1avecA1=2
42 4 6
0 5 70 1 53
5 etb1=2 443 33
5
En terme matriciel, ceci revient à multiplier les systèmeAx=bà gauche par par la matrice triangulaire inférieure
L 1=241 0 0
1 1 00:5 0 13
5L"étape A1 se résume donc à
Ax=b,A1x=b1avecA1=L1A;etb1=L1b:(2)
L1est une matrice triangulaire inférieure inversible à diagonale unité.
Étape A2 :
On éliminex2dans la troisième équation (pour cela, on fait une combinaison linéaire des équations 2 et 3) :
L3 L3 L2=5:(3)
On obtient le système
A2x=b2avecA2=2
41 2 3
0 1 750 0185
3 5 etb2=2 443 185
3 5 (4) 1
En terme matriciel, ceci revient à multiplier les systèmeA1x=b1à gauche par par la matrice triangulaire inférieure
L 2=241 0 0
0 1 001=5 13
5L"étape A2 se résume donc à
A1x=b1,A2x=b2avecA2=L2A1etb2=L2b1:(5)
L2est une matrice triangulaire inférieure inversible à diagonale unité.
Bilan étape A :
La matriceU=A2est une matrice triangulaire supérieure. Ainsi, le systeme(4)(qui peut être réécritUx=b2) est un
système triangulaire supérieur qui va être facile à résoudre à l"étape B. Matriciellement, en combinant(2)et(5)nous pouvons résumer l"étape A comme suit :La matrice
~Lest le produit de deux matrices triangulaires inférieures à diagonales unité. Donc la matrice~Lest une matrice
triangulaire inférieure inversible à diagonale unité. Son inverse, notéeL, est donc aussi triangulaire inférieure à diagonale unité.
On a donc montré queA=LUoùLest une matrice triangulaire inférieure à diagonale unité etUest une matrice triangulaire
supérieure. Autrement dit, la première étape de la méthode du pivot revient à faire de manière implicite la décompositionLU
deA(noter queLy=b, cf. exercice1, question 4).En pratique, lorsqu"on code l"algorithme d"élimination de Gauss, on ne code pas sa version matricielle mais on transforme
progressivement la matriceAet le second membreben faisant combinaisons lineaires des équations (des lignes) (cf.(1)-(3)).
Autrement dit, on n"a pas besoin de calculer pas explicitement la matriceL. Etape B : on résout le système triangulaire supérieurUx=y Ce système est résolu par substitution (cf. exercice 1, question 3). On obtient finalement x=2 412 13 5
Question 1b.
On procède comme dans la question1mais on va voir apparaitre une difficulté supplémentaire due à la présence d"unpivot
nul. On peut remarquer que det2 4 24= 0 si bien que le mineur principal deAd"ordre2est nul.
Étape A : processus d"élimination de Gauss
Étape A1
On éliminex1dans les équations2et3:
L2 L2+L1etL3 L3+12
L1:(7)
On obtient le système
A1x=b1avecA1=2
42 4 6
0 0 70 1 53
5 etb1=2 4127 63
5
En terme matriciel, ceci revient à multiplier les systèmeAx=bà gauche par par la matrice triangulaire inférieure
L 1=241 0 0
1 1 00:5 0 13
5 2L"étape A1 se résume donc à
Ax=b,A1x=b1avecA1=L1A;etb1=L1b:(8)
L1est une matrice triangulaire inférieure inversible à diagonale unité.
Étape A2 : permutation des lignes 2 et 3
Comme le pivotA1(2;2) = 0, on ne peut pas poursuivre directement le processus d"élimination. En particulier, on ne peut
pas éliminerx2dans l"équation3en faisant une combinaison entre la deuxième et la troisième ligne. Cependant, comme
A1(3;2)6= 0, nous allons échanger les lignes2et3.
L2 L3L3 L2:
On obtient alors
A2x=b2avecA2=2
42 4 6
0 1 50 0 73
5 etb2=2 4126 73
5
En terme matriciel, cela revient à multiplier le systèmeA1x=b1par la matrice de permutationP23donnée par
P 23=241 0 0
0 0 10 1 03
5Cette étape A2 se résume donc à
A1x=b1,A2x=b2avecA2=P23A1etb2=P23b1:(9)
Remarque.Comme la matriceA2est de dimension33, il n y a pas besoin de continuer le processus d"élimination (puisque
(A2)3;2= 0). Bien sûr, il faudrait la réaliser dans le cas d"une matrice plus grande. Cela reviendrait alors à multiplier le système
A2x=b2par une matrice triangulaire inférieure.
Bilan étape A
Matriciellement, en combinant(8)-(9), nous pouvons résumer l"étape A comme suit :On remarque queM=P2;3L1=~LP2;3, avec
L=241 0 0
0:5 1 0
1 0 13
5Lest une matrice triangulaire inférieure inversible à diagonale unité. Son inverse, notéeL, est donc aussi triangulaire inférieure
à diagonale unité.
On a donc montré queU=~LP2;3A, c"est à dire que queLU=P2;3A, oùLest une matrice triangulaire inférieure à
diagonale unité,Uest une matrice triangulaire supérieure etP2;3est une matrice de permutation. Autrement dit, la première
étape de la méthode du pivot revient à faire de manière implicite la décompositionPA=LU.
Etape B : on résout le système triangulaire supérieurUx=y Ce système est résolu par substitution (cf. exercice 1, question 3). On obtient finalement x=2 411 13 5
Question 1c.
En reproduisant la technique mise en place dans les questions 1a, 1b, on voit que le systèmeAx=best équivalent au système
suivant : A 1x=b1 3 avec A 1=242 4 6
0 0 70 0 53
5 b1=2 4127 53
5 oub1=2 42
4 53
5
Bien sûr, la matriceA1n"est pas inversible (ce qui signifie d"ailleurs aussi que la matriceAn"est pas inversible) . La deuxième
et la troisième lignes sont liées. Dans le premier cas (b1= (12;7;5)T), le second membre est compatible (i.eb1est orthogonal
à Ker(AT1)). Il y a donc une infinité de solutions données par x=2 411 13 5 +2 42
1 03 5
On remarquera que Ker(A1) =Ker(A) =span(2;1;0)T.
Dans le second cas, (b1= (2;4;5)T), le second membre n"est pas compatible (i.eb1n"est pas orthogonal à Ker(AT1)), il n"y
a pas de solution.Question 2.
4 FonctionElimination(A,b) :U,c[Aest une matrice carrée (inversible),betxsont des vecteurs colonne, Uest un matrice carrée triangulaire supérieure,cest un vecteur colonne.Ce programme transforme un systèmeAx=ben un système équivalentUx=c][Quelques initialisations]" 107[choix de la precision"pour le pivot]n length(b)U A;[On initialise la matriceUpar la matriceA]
c b;[On initialise le vecteurc][On vérifie la compatibilité des dimensions deAetb:]Si(size(A,1)6=nou size(A,2)6=n)AlorsAfficher : "problème dans les tailles des matricesAoub"RetournerU,c;
Fin Si
[Processus d"élimination de Gauss] Pouride1àn1faire[1- On cherche un pivot non nul] k=i;Tant que(jU(k;k)j< "ETkn)fairek=k+ 1 Fait indice=k;[2- On échange la ligneiet la ligneindice][Échange la ligneiet la ligne indice dans la matrice (nécessité d introduire une variable temporaire)]
tempU=U(i;:);U(i;:) =U(indice;:);U(indice;:) =tempU;[Échange la ligne i et la ligne indice dans le second membre]
tempc=c(i);c(i) =c(indice);c(indice) =tempc;[3- On élimine l"inconnue i des equations i+1 à n] pivot=U(i;i);[Test si le pivot est trop petit (matrice possiblement non inversible)] Si(jpivotj< ")Alorsdisp("attention pivot très petit : la matrice est elle inversible?")Fin Si
Pourmdei+1ànfairecoef=U(m;i)=pivot;[Modification de la matrice] U(m;1 :i) = 0;U(m;i+ 1 :n) =U(m;i+ 1 :n)coefU(i;i+ 1 :n);[Modification du second membre] c(m) =c(m)coefc(i);Fin Pour
Fin Pour
Retournerc,U;
FinAlgorithme 1:Algorithme d"élimination de Gauss 5quotesdbs_dbs16.pdfusesText_22[PDF] hamlet texte anglais
[PDF] parties prenantes internes et externes du groupe bic
[PDF] parties prenantes adidas
[PDF] hannah arendt condition de l'homme moderne chapitre 4
[PDF] résolution des triangles quelconques
[PDF] parties prenantes coca cola
[PDF] sncb billet week end jour férié
[PDF] billet shopping sncb 2016
[PDF] prix billet weekend sncb
[PDF] billet shopping sncb 2017
[PDF] ticket weekend sncb prix
[PDF] hannah arendt etat
[PDF] projet de résolution définition
[PDF] exemple de préambule
