1.3 Les méthodes directes
1.3.2 Méthode de Gauss méthode LU. Soit A ∈ Mn(IR) une matrice inversible La factorisation LU de la matrice découle immédiatement de l'algorithme de Gauss.
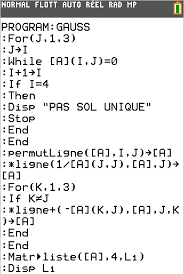Algorithme de la résolution par le pivot de Gauss dun système 3x3
20 oct. 2015 Algorithme de la résolution par le pivot de Gauss d'un système 3x3. 1 La méthode. 1.1 Un exemple. Le but est d'éliminer successivement l ...
Cours 1: Autour des systèmes linéaires Algorithme du pivot de
Une méthode pour inverser une matrice : Pivot de Gauss. L'algorithme général. Remarque importante. Il existe des applications qui n'admettent pas d'inverse
1 Méthode de Gauss et factorisation LU
(c) Résoudre le système (1) par l'algorithme de Gauss avec pivot partiel. (d) Calculer la factorisation ¯L¯U de PA (où P est la matrice produit des matrices de
Cours 1: Autour des systèmes linéaires Algorithme du pivot de Gauss
Methode plus "automatique" : le pivot de Gauss sur les sytémes linéaires. But de l'algorithme. Opérations autorisées. Un exemple avant la "théorie". Mécanismes
Étape A : processus délimination de Gauss
Dans chaque cas on écrira les étapes de la méthode sous forme matricielle. 2. (algo) Soit M ∈ Mn(R) une matrice carrée inversible et soit b ∈ Rn un
S54MA2M7 : Informatique 2 Le pivot de Gauss et al.
5 mars 2019 ▷ A est triangulaire supérieure. Avec l'algorithme de solution des systèmes triangulaires donne une méthode pour résoudre (A
Résolution des syst`emes linéaires Méthode de Gauss
Cet algorithme permet ainsi de calculer rapi- dement
Analyse Numérique
L'algorithme de Gauss Si A est une matrice symétrique définie positive alors la méthode de Gauss-. Seidel converge (la méthode de Jacobi pas forcément).
Informatique en CPGE (2018-2019) Résolution dun système
méthode de Gauss. S. B.. Lycée des EK. 12 mars 2019. S. B. Le principe de l'algorithme du pivot de Gauss est d'exécuter des tâches répétitives qui ...
Algorithme du Pivot de Gauss
Le but de ce cours est l'étude de la résolution de systèmes linéaires. Nous nous intéresserons tout particulièrement à la méthode du pivot de Gauss déjà
Algorithme de la résolution par le pivot de Gauss dun système 3x3
20 oct. 2015 Algorithme de la résolution par le pivot de Gauss d'un système 3x3. 1 La méthode. 1.1 Un exemple. Le but est d'éliminer successivement ...
Résolution des syst`emes linéaires Méthode de Gauss
Méthode de Gauss. Méthodes numériques 2003/2004 - D.Pastre licence de mathématiques et licence MASS Cet algorithme permet ainsi de calculer rapi-.
Étape A : processus délimination de Gauss
Dans chaque cas on écrira les étapes de la méthode sous forme matricielle. 2. (algo) Soit M ? Mn(R) une matrice carrée inversible et soit b ? Rn un
Cours 1: Autour des systèmes linéaires Algorithme du pivot de Gauss
Methode plus "automatique" : le pivot de Gauss sur les sytémes linéaires. Cours 1: Autour des systèmes linéaires. Algorithme du pivot de Gauss. Clément Rau.
Informatique en CPGE (2018-2019) Résolution dun système
12 mars 2019 Algorithme du pivot de Gauss. Utilisation de NumPy. Informatique en CPGE (2018-2019). Résolution d'un système linéaire inversible: méthode ...
Cours 4 : Gauss et LU
par des méthodes directes : Gauss LU
Méthode du pivot de Gauss
Méthode du pivot de Gauss. On veut écrire un algorithme qui: 1. Renvoie l'unique solution de AX = B si A est inversible.
Cours 1: Autour des systèmes linéaires Algorithme du pivot de
Methode plus "automatique" : le pivot de Gauss sur les sytémes linéaires. Introduction aux matrices. Cours 1: Autour des systèmes linéaires. Algorithme du
S54MA2M7 : Informatique 2 Le pivot de Gauss et al.
5 mars 2019 ? A est triangulaire supérieure. Avec l'algorithme de solution des systèmes triangulaires donne une méthode pour résoudre (A
[PDF] Méthode du pivot de Gauss
La méthode du pivot permet d'associer `a tout syst`eme linéaire un syst`eme facile équivalent Elle consiste `a sélectionner une équation qu'on va garder
[PDF] Algorithme du Pivot de Gauss - CPGE du Lycée Montesquieu
Le but de ce cours est l'étude de la résolution de systèmes linéaires Nous nous intéresserons tout particulièrement à la méthode du pivot de Gauss déjà
[PDF] Résolution des syst`emes linéaires Méthode de Gauss - Normale Sup
Méthode de Gauss Méthodes numériques 2003/2004 - D Pastre licence de mathématiques et licence MASS Cet algorithme permet ainsi de calculer rapi-
[PDF] Chapitre V La méthode du pivot de Gauss et ses applications
- Intervertir deux équations : - Intervertir l'ordre des inconnues - Remplacer une équation par La technique du pivot : On décrit l'algorithme qui permet
[PDF] METHODE DU PIVOT DE GAUSS - Toutes les Maths
METHODE DU PIVOT DE GAUSS La méthode du pivot de Gauss permet la résolution générale des systèmes d'équations linéaires à n équations et p inconnues
[PDF] Cours 1: Autour des systèmes linéaires Algorithme du pivot de Gauss
Méthode par substitution Méthode par addition 3 Methode plus "automatique" : le pivot de Gauss sur les sytémes linéaires But de l'algorithme
[PDF] Algorithme de la résolution par le pivot de Gauss dun système 3x3
20 oct 2015 · Algorithme de la résolution par le pivot de Gauss d'un système 3x3 1 La méthode 1 1 Un exemple Le but est d'éliminer successivement
[PDF] Chapitre 2 Résolution des Systèmes Linéaires Ax=b Méthodes
Soit un système linéaire Ax = b l'algorithme de Gauss sans pivotation est la méthode classique de substitution La matrice d'origine A est d'abord
[PDF] 13 Les méthodes directes
La factorisation LU de la matrice découle immédiatement de l'algorithme de Gauss Voyons comment sur l'exem- ple précédent
[PDF] XI Algorithme de Gauss-Jordan - Emmanuel Morand
Algorithme de Gauss-Jordan 1 Opérations élémentaires sur les lignes d'une matrice Définition 1 On définit trois types d'opérations élémentaires sur les
Comment faire la méthode de Gauss ?
La méthode du pivot de Gauss est une méthode pour transformer un système en un autre système équivalent (ayant les mêmes solutions) qui est triangulaire et est donc facile à résoudre. Les opérations autorisées pour transformer ce système sont : échange de deux lignes. multiplication d'une ligne par un nombre non nul.Quelle est la formule du pivot de Gauss ?
La méthode du pivot permet d'associer `a tout syst`eme linéaire un syst`eme facile équivalent. ? 2x + 3y + z = 1 ?7y + 7z = 1 ?7y ? 3z = ?2. on résout le syst`eme dérivé (par combinaison linéaire) et on conclut avec l'équation facile.Qu'est-ce qu'un pivot maths ?
Définition - Une matrice est échelonnée si le nombre de 0 au début de chaque ligne est strictement croissant quand on passe d'une ligne à la suivante. Le premier élément non nul de chaque ligne dans une matrice échelonnée s'appelle le pivot.- La transformation de Gauss-Jordan consiste à transformer ce système en un système équivalent dont le bloc gauche est l'identité, c'est-à-dire qu'il faut modifier la matrice (A I) pour qu'elle devienne de la forme (I A ? 1) en utilisant les propriétés de l'algorithme.
Méthode du pivot de Gauss
Informatique pour tous
Méthode du pivot de Gauss
On veut résoudre un système linéaire denéquations àninconnues de la forme: (S): a1,1x1+···+a1,nxn=b1 an,1x1+···+an,nxn=bn On peut écrire ces équations sous forme matricielle : (S)?AX=B avecA= a1,1a1,2···a1,n a2,1a2,2···a2,n an,1an,2···an,n )))),X= x1 x2 xn ))))etB= b1 b2 bnMéthode du pivot de Gauss
On veut résoudre un système linéaire denéquations àninconnues de la forme: (S): a1,1x1+···+a1,nxn=b1 an,1x1+···+an,nxn=bn On peut écrire ces équations sous forme matricielle : (S)?AX=B avecA= a1,1a1,2···a1,n a2,1a2,2···a2,n an,1an,2···an,n )))),X= x1 x2 xn ))))etB= b1 b2 bnMéthode du pivot de Gauss
La méthode du pivot de Gauss comporte 2 grandes étapes :1échelonnement du système(descente),
2réduction du système(remontée).
´Etapes réalisées avec desopérations élémentaires sur les lignes:Li←λLiavecλ?= 0,
Lj←Lj+λLiaveci?=j,
Li↔Lj.
Appliquer des opérations élémentaires à un système d"équations ne change pas ses solutions.Méthode du pivot de Gauss
La méthode du pivot de Gauss comporte 2 grandes étapes :1échelonnement du système(descente),
2réduction du système(remontée).
´Etapes réalisées avec desopérations élémentaires sur les lignes:Li←λLiavecλ?= 0,
Lj←Lj+λLiaveci?=j,
Li↔Lj.
Appliquer des opérations élémentaires à un système d"équations ne change pas ses solutions.Méthode du pivot de Gauss
La méthode du pivot de Gauss comporte 2 grandes étapes :1échelonnement du système(descente),
2réduction du système(remontée).
´Etapes réalisées avec desopérations élémentaires sur les lignes:Li←λLiavecλ?= 0,
Lj←Lj+λLiaveci?=j,
Li↔Lj.
Appliquer des opérations élémentaires à un système d"équations ne change pas ses solutions.Matrice augmentée
(S): a1,1x1+···+a1,nxn=b1 an,1x1+···+an,nxn=bn Il est pratique de considérer lamatrice augmentéedu système (S): (A|B) = a1,1a1,2···a1,nb1 a2,1a2,2···a2,nb2 an,1an,2···an,nbnMéthode du pivot de Gauss
On veut écrire un algorithme qui:
1Renvoie l"unique solution deAX=B, siAest inversible.
2Sinon, indique queAn"est pas inversible (il peut donc exister
aucune solution ou une infinité de solutions).Méthode du pivot de Gauss
On veut écrire un algorithme qui:
1Renvoie l"unique solution deAX=B, siAest inversible.
2Sinon, indique queAn"est pas inversible (il peut donc exister
aucune solution ou une infinité de solutions).Descente
(A|B) = a1,1a1,2···a1,nb1 a2,1a2,2···a2,nb2 an,1an,2···an,nbn1Première étape :
Si nécessaire, échanger 2 lignes de façon à avoira1,1?= 0. On effectue des opérationsLi←Li+λL1pouriallant de 2 ànde manière à mettre des zéros sur la 1ère colonne, en dessous de la diagonale.( a?1,1a?1,2···a?1,n-1a?1,nb?10a?2,2···a?2,n-1a?2,nb?2
0a?3,2···a?3,n-1a?3,nb?3
0a?n,2···a?n,n-1a?n,nb?n
Descente
(A|B) = a1,1a1,2···a1,nb1 a2,1a2,2···a2,nb2 an,1an,2···an,nbn1Première étape :
Si nécessaire, échanger 2 lignes de façon à avoira1,1?= 0. On effectue des opérationsLi←Li+λL1pouriallant de 2 ànde manière à mettre des zéros sur la 1ère colonne, en dessous de la diagonale.( a?1,1a?1,2···a?1,n-1a?1,nb?10a?2,2···a?2,n-1a?2,nb?2
0a?3,2···a?3,n-1a?3,nb?3
0a?n,2···a?n,n-1a?n,nb?n
Descente
(A|B) = a1,1a1,2···a1,nb1 a2,1a2,2···a2,nb2 an,1an,2···an,nbn1Première étape :
Si nécessaire, échanger 2 lignes de façon à avoira1,1?= 0. On effectue des opérationsLi←Li+λL1pouriallant de 2 ànde manière à mettre des zéros sur la 1ère colonne, en dessous de la diagonale.( a?1,1a?1,2···a?1,n-1a?1,nb?10a?2,2···a?2,n-1a?2,nb?2
0a?3,2···a?3,n-1a?3,nb?3
0a?n,2···a?n,n-1a?n,nb?n
Descente
a?1,1a?1,2···a?1,n-1a?1,nb?10a?2,2···a?2,n-1a?2,nb?2
0a?3,2···a?3,n-1a?3,nb?3
0a?n,2···a?n,n-1a?n,nb?n
2Deuxième étape : on recommence avec la 2ème colonne
recherche d"un deuxième pivot non nula??2,2élimination des termes sous le pivot( a?1,1a?1,2···a?1,n-1a?1,nb?10a??2,2···a??2,n-1a??2,nb??2
0 0···a??3,n-1a??3,nb??3
0 0···a??n,n-1a??n,nb??n
Descente
a?1,1a?1,2···a?1,n-1a?1,nb?10a?2,2···a?2,n-1a?2,nb?2
0a?3,2···a?3,n-1a?3,nb?3
0a?n,2···a?n,n-1a?n,nb?n
2Deuxième étape : on recommence avec la 2ème colonne
recherche d"un deuxième pivot non nula??2,2élimination des termes sous le pivot( a?1,1a?1,2···a?1,n-1a?1,nb?10a??2,2···a??2,n-1a??2,nb??2
0 0···a??3,n-1a??3,nb??3
0 0···a??n,n-1a??n,nb??n
Descente
3Étapes suivantes : on recommence le processus afin d"obtenir une
matrice échelonnée( a?1,1a?1,2···a?1,n-1a?1,nb?10a?2,2···a?2,n-1a?2,nb?2
0 0···a?3,n-1a?3,nb?3
0 0···0a?n,nb?n
Remarque : s"il n"est pas possible de trouver un pivot (non nul) sur la iemecolonne dans les lignesLiàLn, la matriceAn"est pas inversible, on interrompt l"algorithme et on retourne un message d"erreur.Descente
3Étapes suivantes : on recommence le processus afin d"obtenir une
matrice échelonnée( a?1,1a?1,2···a?1,n-1a?1,nb?10a?2,2···a?2,n-1a?2,nb?2
0 0···a?3,n-1a?3,nb?3
0 0···0a?n,nb?n
Remarque : s"il n"est pas possible de trouver un pivot (non nul) sur la iemecolonne dans les lignesLiàLn, la matriceAn"est pas inversible, on interrompt l"algorithme et on retourne un message d"erreur.Remontée
1Par multiplication de chaque ligneLipar1
a?i,i, on met des 1 sur la diagonale.2On met des 0 au dessus de la diagonale de la dernière colonne.
1a??1,2···a??1,n-10b??1
0 1···a??2,n-10b??2
0 0···a??3,n-10b??3
0 0···0 1b??n
3On fait de même sur les autres colonnes, de droite à gauche.
Remontée
1Par multiplication de chaque ligneLipar1
a?i,i, on met des 1 sur la diagonale.2On met des 0 au dessus de la diagonale de la dernière colonne.
1a??1,2···a??1,n-10b??1
0 1···a??2,n-10b??2
0 0···a??3,n-10b??3
0 0···0 1b??n
3On fait de même sur les autres colonnes, de droite à gauche.
Remontée
A l"issue de ces opérations, on aboutit à une matrice augmentéeéchelonnée et réduite du type :
1 0···0 0b??10 1···0 0b??20 0···0 0b??3··· ··· ··· ··· ··· ···
0 0···0 1b??n
La solution du systèmeAX=Best alorsX=
b??1b??2b??3··· b??nRemontée
A l"issue de ces opérations, on aboutit à une matrice augmentéeéchelonnée et réduite du type :
1 0···0 0b??10 1···0 0b??20 0···0 0b??3··· ··· ··· ··· ··· ···
0 0···0 1b??n
La solution du systèmeAX=Best alorsX=
b??1b??2b??3··· b??nComment déterminerA-1?
On peut utiliser la matrice augmentée : (A|In)
(A|In) = a1,1a1,2···a1,n1 0···0 a2,1a2,2···a2,n0 1···0 an,1an,2···an,n0 0···1 Après échelonnement et réduction du système on obtient : (In|A-1) =1 0···0c1,1c1,2···c1,n
0 1···0c2,1c2,2···c2,n
0 0···1cn,1cn,2···cn,n
On peut finalement extraireA-1=
c1,1c1,2···c1,n c2,1c2,2···c2,n cn,1cn,2···cn,nComment déterminerA-1?
On peut utiliser la matrice augmentée : (A|In)
(A|In) = a1,1a1,2···a1,n1 0···0 a2,1a2,2···a2,n0 1···0 an,1an,2···an,n0 0···1 Après échelonnement et réduction du système on obtient : (In|A-1) =1 0···0c1,1c1,2···c1,n
0 1···0c2,1c2,2···c2,n
0 0···1cn,1cn,2···cn,n
On peut finalement extraireA-1=
c1,1c1,2···c1,n c2,1c2,2···c2,n cn,1cn,2···cn,nComment déterminerA-1?
On peut utiliser la matrice augmentée : (A|In)
(A|In) = a1,1a1,2···a1,n1 0···0 a2,1a2,2···a2,n0 1···0 an,1an,2···an,n0 0···1 Après échelonnement et réduction du système on obtient : (In|A-1) =1 0···0c1,1c1,2···c1,n
0 1···0c2,1c2,2···c2,n
0 0···1cn,1cn,2···cn,n
On peut finalement extraireA-1=
c1,1c1,2···c1,n c2,1c2,2···c2,n cn,1cn,2···cn,n Nous allons implémenter la méthode de Gauss en TP.Les matrices seront des tableaux 2D numpy.
Exercice
Écrire une fonctionechangetelle queechange(M, i, j)échange les lignesietjdeM(Li↔Lj). Nous allons implémenter la méthode de Gauss en TP.Les matrices seront des tableaux 2D numpy.
Exercice
Écrire une fonctionechangetelle queechange(M, i, j)échange les lignesietjdeM(Li↔Lj).Exercice
Écrire une fonctionechangetelle queechange(M, i, j)échange les lignesietjdeM.1ère possibilité:
Exercice
Écrire une fonctionechangetelle queechange(M, i, j)échange les lignesietjdeM.2ème possibilité:
Exercice
Écrire une fonctiondilatationtelle quedilatation(M, i, a) réalise l"opérationLi←aLi.Exercice
Écrire une fonctiontransvectiontelle que
transvection(M, i, j, a)réalise l"opérationLi←Li+a×Lj.Exercice
Écrire une fonctionpivottelle quepivot(M, j)renvoie une ligne d"un coefficient non nul sous la diagonale de lajème colonne.Exercice
Écrire une fonctionechelonnerréalisant la descente du pivot deGauss.
Complexité de la méthode du pivot de Gauss
On veut résoudreAX=B, avecAune matricen×n.
1Construire la matrice augmentée
2Descente: pour toute colonne, de gauche à droite...
Trouver un pivot
Mettre ce pivot sur la diagonale
Mettre des 0 en dessous de la diagonale
3Remontée: pour toute colonne, de droite à gauche...
Mettre des 0 au dessus de la diagonale
Quelle est la complexité de la méthode du pivot de Gauss? On compte les multiplications et additions.Complexité de la méthode du pivot de Gauss
On veut résoudreAX=B, avecAune matricen×n.
1Construire la matrice augmentéeO(n2) car il faut remplir une
matricen×(n+ 1)2Descente: pour toute colonne, de gauche à droite...
Trouver un pivot
Mettre ce pivot sur la diagonale
Mettre des 0 en dessous de la diagonale
3Remontée: pour toute colonne, de droite à gauche...
Mettre des 0 au dessus de la diagonale
Quelle est la complexité de la méthode du pivot de Gauss?Complexité de la méthode du pivot de Gauss
On veut résoudreAX=B, avecAune matricen×n.
1Construire la matrice augmentéeO(n2)
2Descente: pour toute colonne, de gauche à droite...
Trouver un pivotO(n) pour parcourir toutes les lignes en dessous de la diagonaleMettre ce pivot sur la diagonale
Mettre des 0 en dessous de la diagonale
3Remontée: pour toute colonne, de droite à gauche...
Mettre des 0 au dessus de la diagonale
Quelle est la complexité de la méthode du pivot de Gauss?Complexité de la méthode du pivot de Gauss
On veut résoudreAX=B, avecAune matricen×n.
1Construire la matrice augmentéeO(n2)
2Descente: pour toute colonne, de gauche à droite...
Trouver un pivotO(n)
Mettre ce pivot sur la diagonaleO(n) pour échanger 2 lignesMettre des 0 en dessous de la diagonale
3Remontée: pour toute colonne, de droite à gauche...
Mettre des 0 au dessus de la diagonale
Quelle est la complexité de la méthode du pivot de Gauss?Complexité de la méthode du pivot de Gauss
On veut résoudreAX=B, avecAune matricen×n.
1Construire la matrice augmentéeO(n2)
2Descente: pour toute colonne, de gauche à droite...
Trouver un pivotO(n)
Mettre ce pivot sur la diagonaleO(n)
Mettre des 0 en dessous de la diagonaleO(n2) car il faut faire au plusntransvections3Remontée: pour toute colonne, de droite à gauche...
Mettre des 0 au dessus de la diagonale
Quelle est la complexité de la méthode du pivot de Gauss?Complexité de la méthode du pivot de Gauss
On veut résoudreAX=B, avecAune matricen×n.
1Construire la matrice augmentéeO(n2)
2Descente enn×(O(n) +O(n) +O(n2)) =O(n3): pour
toute colonne, de gauche à droite...Trouver un pivotO(n)
Mettre ce pivot sur la diagonaleO(n)
Mettre des 0 en dessous de la diagonaleO(n2)
3Remontée: pour toute colonne, de droite à gauche...
Mettre des 0 au dessus de la diagonale
Quelle est la complexité de la méthode du pivot de Gauss?Complexité de la méthode du pivot de Gauss
On veut résoudreAX=B, avecAune matricen×n.
1Construire la matrice augmentéeO(n2)
2Descente enO(n3): pour toute colonne, de gauche à droite...
Trouver un pivotO(n)
Mettre ce pivot sur la diagonaleO(n)
Mettre des 0 en dessous de la diagonaleO(n2)
3Remontée: pour toute colonne, de droite à gauche...
Mettre des 0 au dessus de la diagonaleO(n2) car il faut faire au plusntransvections Quelle est la complexité de la méthode du pivot de Gauss?Complexité de la méthode du pivot de Gauss
On veut résoudreAX=B, avecAune matricen×n.
1Construire la matrice augmentéeO(n2)
2Descente enO(n3): pour toute colonne, de gauche à droite...
Trouver un pivotO(n)
Mettre ce pivot sur la diagonaleO(n)
Mettre des 0 en dessous de la diagonaleO(n2)
3Remontée enn×O(n2): pour toute colonne, de droite à
gauche... Mettre des 0 au dessus de la diagonaleO(n2) car il faut faire au plusntransvections Quelle est la complexité de la méthode du pivot de Gauss?Complexité de la méthode du pivot de Gauss
On veut résoudreAX=B, avecAune matricen×n.
1Construire la matrice augmentéeO(n2)
quotesdbs_dbs44.pdfusesText_44[PDF] hamlet texte anglais
[PDF] parties prenantes internes et externes du groupe bic
[PDF] parties prenantes adidas
[PDF] hannah arendt condition de l'homme moderne chapitre 4
[PDF] résolution des triangles quelconques
[PDF] parties prenantes coca cola
[PDF] sncb billet week end jour férié
[PDF] billet shopping sncb 2016
[PDF] prix billet weekend sncb
[PDF] billet shopping sncb 2017
[PDF] ticket weekend sncb prix
[PDF] hannah arendt etat
[PDF] projet de résolution définition
[PDF] exemple de préambule
