 Chapitre 1. Ensembles et applications.
Chapitre 1. Ensembles et applications.
18 févr. 2013 Soit f : A −→ B une application. Le sous-ensemble. {(xf (x))
 Chapitre 2 Ensembles et sous-ensembles
Chapitre 2 Ensembles et sous-ensembles
Ensembles et sous-ensembles. 1. Notion d'ensemble - Elément d'un ensemble. Dans une théorie mathématique il est rare qu'un objet intervienne seul ; d'o`u l
 Cours de mathématiques - Exo7
Cours de mathématiques - Exo7
Nous avons déjà vu que ceci est un espace vectoriel. Mini-exercices. Parmi les ensembles suivants reconnaître ceux qui sont des sous-espaces vectoriels : 1. (x
 COMBINATOIRE ET DÉNOMBREMENT
COMBINATOIRE ET DÉNOMBREMENT
×2 ( facteurs) possibilités d'obtenir un sous-ensemble de soit 2 . Exemple www.maths-et-tiques.fr/index.php/mentions-legales.
 Cours : Ensembles et applications
Cours : Ensembles et applications
les mathématiques sur des bases logiques. Il reçut une lettre d'un tout jeune cl(x) est donc un sous-ensemble de E on le note aussi x. Si y ∈ cl(x)
 [PDF] Groupes - Exo7 - Cours de mathématiques
[PDF] Groupes - Exo7 - Cours de mathématiques
4. Montrer que l'ensemble des matrices 2×2 de déterminant 1 ayant leurs coefficients dans Z est un sous-groupe de (Gl2×)
 Analyse combinatoire
Analyse combinatoire
6 mars 2008 Mathématiques Générales B. Université de Gen`eve. Sylvain Sardy. 6 mars ... – Combien y a-t-il de sous-ensembles d'un ensemble de cardinalité n?
 THÉORIE DES ENSEMBLES
THÉORIE DES ENSEMBLES
Soit Ω l'ensemble des nombres possibles d'obtenir de la somme de deux dés. Ω. 2
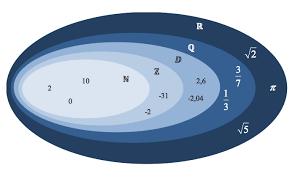 ENSEMBLES DE NOMBRES
ENSEMBLES DE NOMBRES
sous forme d'un intervalle : 2xГ3<4. 0 1. 0 1. 0 1. 0 1. 0 1. 0 1. 0 1. 0 1. Page 5. 5 sur 8. Yvan Monka – Académie de Strasbourg – www.maths-et-tiques.fr. 2xГ3 ...
 Chapitre 1 Ensembles et sous-ensembles
Chapitre 1 Ensembles et sous-ensembles
sous-ensembles d'un ensemble E. ... Il peut contenir des mots utilisés dans un sens différent du sens courant ou des mots spécifiques au langage mathématique.
 Chapitre 1 Ensembles et sous-ensembles
Chapitre 1 Ensembles et sous-ensembles
2?) Soit E un ensemble qui est la réunion de deux sous-ensembles on s'efforce souvent de les écrire en utilisant des symboles mathématiques.
 ENSEMBLES DE NOMBRES
ENSEMBLES DE NOMBRES
Un nombre rationnel peut s'écrire sous la forme d'un quotient a b avec a un entier et b un entier non nul. L'ensemble des nombres rationnels est noté ?.
 Cours : Ensembles et applications
Cours : Ensembles et applications
les mathématiques sur des bases logiques. Il reçut une lettre d'un tout jeune mathématicien : « J'ai bien lu votre premier.
 Cours de mathématiques - Exo7
Cours de mathématiques - Exo7
Sous-groupes. Montrer qu'un ensemble est un groupe à partir de la définition peut être assez long. Il existe une autre technique c'est de montrer qu'un
 Cours de mathématiques - Exo7
Cours de mathématiques - Exo7
L'ensemble F1 = (x y) ? 2
 Chapitre 1. Ensembles et applications.
Chapitre 1. Ensembles et applications.
18 févr. 2013 Soit f : A ?? B une application. Le sous-ensemble. {(xf (x))
 COMBINATOIRE ET DÉNOMBREMENT
COMBINATOIRE ET DÉNOMBREMENT
Alors est l'ensemble des couples possibles pour deux dés. On a par exemple : Page 3. Yvan Monka – Académie de Strasbourg – www.maths-et
 Chapitre 1 Ensembles et sous-ensembles
Chapitre 1 Ensembles et sous-ensembles
Ensembles et sous-ensembles. 1. Notion d'ensemble - Elément d'un ensemble. Un ensemble est une collection d'objets satisfaisant un certain nombre de
 Analyse combinatoire
Analyse combinatoire
6 mars 2008 Mathématiques Générales B. Université de Gen`eve ... distincts est un sous-ensemble `a k éléments de cet ensemble. Les éléments sont.
 Chapitre 2 Ensembles et sous-ensembles
Chapitre 2 Ensembles et sous-ensembles
Ensembles et sous-ensembles. 1. Notion d'ensemble - Elément d'un ensemble. Dans une théorie mathématique il est rare qu'un objet intervienne seul ; d'o`u
 [PDF] Chapitre 1 Ensembles et applications
[PDF] Chapitre 1 Ensembles et applications
18 fév 2013 · Pour un ensemble A l'ensemble de tous les sous-ensembles de A est noté 2A ou P(A) Exemple Soit A = {01} Les sous-ensembles de A sont ? A
 [PDF] Chapitre 1 Ensembles et sous-ensembles - Université de Rennes
[PDF] Chapitre 1 Ensembles et sous-ensembles - Université de Rennes
Définition 1 3 – Soient A et B deux sous-ensembles d'un ensemble E L'ensemble {x x ? A et x ? B} est appelé l'intersection des ensembles A
 [PDF] ensemblepdf
[PDF] ensemblepdf
Un ensemble est une collection d'objets satisfaisant un certain nombre de propriétés et chacun de ces objets est appelé élément de cet ensemble
 [PDF] THÉORIE DES ENSEMBLES
[PDF] THÉORIE DES ENSEMBLES
L'ensemble est dit un sous-ensemble de si et seulement si tous les éléments de sont aussi des éléments de On dit alors que l'ensemble est inclus dans l'
 [PDF] 1 Ensembles - Apprendre-en-lignenet
[PDF] 1 Ensembles - Apprendre-en-lignenet
Un sous-ensemble est un ensemble dont chaque élément est aussi contenu dans un autre ensemble Si A est un sous-ensemble de B on note A?B Par exemple si J
 [PDF] ENSEMBLES DE NOMBRES - maths et tiques
[PDF] ENSEMBLES DE NOMBRES - maths et tiques
Un nombre rationnel peut s'écrire sous la forme d'un quotient a b avec a un entier et b un entier non nul L'ensemble des nombres rationnels est noté ?
 [PDF] Généralités sur les ensembles - livres-mathematiquesfr
[PDF] Généralités sur les ensembles - livres-mathematiquesfr
Un des probl`emes qui nous intéressera rapidement est de déterminer tous les sous-ensembles d'un ensemble fini donné Pour cela nous avons besoin d'un ensemble
 [PDF] Introduction à la notion densembles - Université de Toulouse
[PDF] Introduction à la notion densembles - Université de Toulouse
Un ensemble est une collection d'objets deux à deux distincts appelés éléments On peut définir un ensemble de deux manières : en extension : on donne la liste
 [PDF] Ensembles et applications - Exo7 - Cours de mathématiques
[PDF] Ensembles et applications - Exo7 - Cours de mathématiques
que E est un sous-ensemble de F ou une partie de F • L'égalité E = F si et seulement si E ? F et F ? E • Ensemble des parties de E On note
 [PDF] Théorie des ensembles
[PDF] Théorie des ensembles
que pour tout ? ? E ? soit un sous-ensemble de E Voici un exemple : mathématique sur des ensembles qui s'exprime en quantifiant les variables et les
C'est quoi un sous-ensemble en maths ?
Étant donné un ensemble E; un sous-ensemble de E est un ensemble dont tous les éléments appartiennent à l'ensemble E. Synonyme de partie d'un ensemble. Un sous-ensemble propre ou strict d'un ensemble E est un sous-ensemble de E qui n'est pas égal à E.Quels sont les sous-ensembles ?
Un sous-ensemble est aussi un ensemble. Soient deux ensembles A et B. On dit que B est un sous-ensemble de A si tous les éléments de B sont aussi éléments de A. Exemple : L'ensemble B des entiers naturels de 1 à 3 est un sous-ensemble de l'ensemble A constitué par les entiers naturels de 1 à 7.Comment montrer qu'un ensemble est un sous-ensemble ?
Pour démontrer que F est un sous-espace vectoriel de E , on applique la caractérisation des sous-espaces vectoriels, c'est-à-dire qu'on vérifie que 0E?F 0 E ? F et que, pour tout couple (x,y)?F2 ( x , y ) ? F 2 et tout scalaire ??K ? ? K , on a {x+y?F?x?F.- On dit que A est inclus dans B si chaque élément de A est un élément de B. On note A ? B. On dit aussi “A est contenu dans B” ou “A est une partie de B” ou “A est un sous-ensemble de B”. Remarques - • A ? A • Si A ? B et B ? C, alors A ? C • A = B si et seulement si (A ? B et B ? A).
Ensembles et applications
MotivationsAu début duXXesiècle le professeur Frege peaufinait la rédaction du second tome d"un ouvrage qui souhaitait refonder
les mathématiques sur des bases logiques. Il reçut une lettre d"un tout jeune mathématicien :" J"ai bien lu votre premier
livre. Malheureusement vous supposez qu"il existe un ensemble qui contient tous les ensembles. Un tel ensemble ne peut
exister. »S"ensuit une démonstration de deux lignes. Tout le travail de Frege s"écroulait et il ne s"en remettra jamais.
Le jeune Russell deviendra l"un des plus grands logiciens et philosophes de son temps. Il obtient le prix Nobel de
littérature en 1950.Voici le " paradoxe de Russell » pour montrer que l"ensemble de tous les ensembles ne peut exister. C"est très bref,
mais difficile à appréhender. Par l"absurde, supposons qu"un tel ensembleEcontenant tous les ensembles existe.
Considérons
F=¦
E∈ E |E/∈E©
Expliquons l"écritureE/∈E: leEde gauche est considéré comme un élément, en effet l"ensembleEest l"ensemble de
tous les ensembles etEest un élément de cet ensemble; leEde droite est considéré comme un ensemble, en effet les
élément deEsont des ensembles! On peut donc s"interroger si l"élémentEappartient à l"ensembleE. Si non, alors
par définition on metEdans l"ensembleF.La contradiction arrive lorsque l"on se pose la question suivante : a-t-onF∈FouF/∈F? L"une des deux affirmation
doit être vraie. Et pourtant :SiF∈Falors par définition deF,Fest l"un des ensemblesEtel queF/∈F. Ce qui est contradictoire.
SiF/∈FalorsFvérifie bien la propriété définissantFdoncF∈F! Encore contradictoire.
Aucun des cas n"est possible. On en déduit qu"il ne peut exister un tel ensembleEcontenant tous les ensembles.
Ce paradoxe a été popularisé par l"énigme suivante :" Dans une ville, le barbier rase tous ceux qui ne se rasent pas
eux-mêmes. Qui rase le barbier? »La seule réponse valable est qu"une telle situation ne peut exister.
Ne vous inquiétez pas, Russell et d"autres ont fondé la logique et les ensembles sur des bases solides. Cependant il
n"est pas possible dans ce cours de tout redéfinir. Heureusement, vous connaissez déjà quelques ensembles :
l"ensemble des entiers naturelsN={0,1,2,3,...}. l"ensemble des entiers relatifsZ={...,-2,-1,0,1,2,...}. l"ensemble des rationnelsQ=pq |p∈Z,q∈N\{0}. l"ensemble des réelsR, par exemple 1,p2,π, ln(2),... l"ensemble des nombres complexesC.ENSEMBLES ET APPLICATIONS1. ENSEMBLES2Nous allons essayer de voir les propriétés des ensembles, sans s"attacher à un exemple particulier. Vous vous apercevrez
assez rapidement que ce qui est au moins aussi important que les ensembles, ce sont les relations entre ensembles : ce
sera la notion d"application (ou fonction) entre deux ensembles.1. Ensembles
1.1. Définir des ensembles
On va définir informellement ce qu"est un ensemble : unensembleest une collection d"éléments.
Exemples :
{0,1},{rouge,noir},{0,1,2,3,...}=N.Un ensemble particulier est l"ensemble vide, noté∅qui est l"ensemble ne contenant aucun élément.
On notex∈Esixest un élément deE, etx/∈Edans le cas contraire.Voici une autre façon de définir des ensembles : une collection d"éléments qui vérifient une propriété.
Exemples :x∈R| |x-2|<1,z∈C|z5=1,x∈R|0⩽x⩽1= [0,1].1.2. Inclusion, union, intersection, complémentaire
L"inclusion.E⊂Fsi tout élément deEest aussi un élément deF. Autrement dit :∀x∈E(x∈F). On dit alors
queEest unsous-ensembledeFou unepartiedeF. L"égalité.E=Fsi et seulement siE⊂FetF⊂E. Ensemble des partiesdeE. On noteP(E)l"ensemble des parties deE. Par exemple siE={1,2,3}: P({1,2,3}) =∅,{1},{2},{3},{1,2},{1,3},{2,3},{1,2,3}.Complémentaire. SiA⊂E,∁
EA=x∈E|x/∈AOn le note aussiE\Aet juste∁As"il n"y a pas d"ambiguïté (et parfois aussiAcouA).A∁
EAEUnion. PourA,B⊂E,A∪B=x∈E|x∈Aoux∈BLe" ou »n"est pas exclusif :xpeut appartenir àAet àBen même temps.ABA∪B
ENSEMBLES ET APPLICATIONS1. ENSEMBLES3
1.3. Règles de calculs
SoientA,B,Cdes parties d"un ensembleE.
A∩B=B∩A
A∩(B∩C) = (A∩B)∩C(on peut donc écrireA∩B∩Csans ambigüité)A∪B=B∪A
A∪(B∪C) = (A∪B)∪C(on peut donc écrireA∪B∪Csans ambiguïté)A∩(B∪C) = (A∩B)∪(A∩C)A∪(B∩C) = (A∪B)∩(A∪C)
∁∁A=Aet doncA⊂B⇐⇒∁B⊂∁A ∁(A∩B) =∁A∪∁B ∁(A∪B) =∁A∩∁BVoici les dessins pour les deux dernières assertions.AB∁AAB∁BABA∩B∁(A∩B) =∁A∪∁BABA∪B∁(A∪B) =∁A∩∁BLes preuves sont pour l"essentiel une reformulation des opérateurs logiques, en voici quelques-unes :
Preuve deA∩(B∪C) = (A∩B)∪(A∩C):x∈A∩(B∪C)⇐⇒x∈Aetx∈(B∪C)⇐⇒x∈Aet(x∈Boux∈
Preuve de∁(A∩B)=∁A∪∁B:x∈∁(A∩B)⇐⇒x/∈(A∩B)⇐⇒nonx∈A∩B⇐⇒nonx∈Aetx∈
B⇐⇒non(x∈A)ou non(x∈B)⇐⇒x/∈Aoux/∈B⇐⇒x∈∁A∪∁B.
Remarquez que l"on repasse aux éléments pour les preuves.1.4. Produit cartésien
SoientEetFdeux ensembles. Leproduit cartésien, notéE×F, est l"ensemble des couples(x,y)oùx∈Eety∈F.
Exemple 1.
1.V ousconnaissez R2=R×R=(x,y)|x,y∈R.
2. Autre exemple [0,1]×R=(x,y)|0⩽x⩽1,y∈RENSEMBLES ET APPLICATIONS2. APPLICATIONS4xy
013.[0,1]×[0,1]×[0,1] =(x,y,z)|0⩽x,y,z⩽1xy
z 011 1Mini-exercices.
1. En utilisant les définitions, montrer : A̸=Bsi et seulement s"il existea∈A\Boub∈B\A. 2.Énumérer P({1,2,3,4}).
3. Montrer A∪(B∩C) = (A∪B)∩(A∪C)et∁(A∪B) =∁A∩∁B. 4.Énumérer {1,2,3}×{1,2,3,4}.
5.Représenter les sous-ensembles deR2suivants :]0,1[∪[2,3[×[-1,1],R\(]0,1[∪[2,3[)×(R\[-1,1])∩
[0,2].2. Applications2.1. Définitions
Uneapplication(ou unefonction)f:E→F, c"est la donnée pour chaque élémentx∈Ed"un unique élément de
Fnotéf(x).
Nous représenterons les applications par deux types d"illustrations : les ensembles " patates », l"ensemble de départ
(et celui d"arrivée) est schématisé par un ovale ses éléments par des points. L"associationx7→f(x)est représentée
par une flèche.xf(x)EFfL"autre représentation est celle des fonctions continues deRdansR(ou des sous-ensembles deR). L"ensemble de
départRest représenté par l"axe des abscisses et celui d"arrivée par l"axe des ordonnées. L"associationx7→f(x)
est représentée par le point(x,f(x)).ENSEMBLES ET APPLICATIONS2. APPLICATIONS5xy
xf(x)Égalité. Deux applicationsf,g:E→Fsont égales si et seulement si pour toutx∈E,f(x) =g(x). On note alors
f=g.Legraphedef:E→FestΓ
f=¦x,f(x)∈E×F|x∈E©xy fComposition. Soientf:E→Fetg:F→Galorsg◦f:E→Gest l"application définie parg◦f(x) =gf(x).EFGfg
g◦f Restriction. Soientf:E→FetA⊂Ealors la restriction defàAest l"application f |A:A-→F x7-→f(x)Exemple 2.
1.L "identité, idE:E→Eest simplement définie parx7→xet sera très utile dans la suite.
2.Définissons f,gainsi
f:]0,+∞[-→]0,+∞[ x7-→1x ,g:]0,+∞[-→R x7-→x-1x+1. Alorsg◦f:]0,+∞[→Rvérifie pour toutx∈]0,+∞[: =1x -11 x +1=1-x1+x=-g(x).2.2. Image directe, image réciproque
SoientE,Fdeux ensembles.Définition 1.
SoitA⊂Eetf:E→F, l"image directedeAparfest l"ensemblef(A) =f(x)|x∈AENSEMBLES ET APPLICATIONS2. APPLICATIONS6EF
Af(A)f
xyAf(A)Définition 2.
SoitB⊂Fetf:E→F, l"image réciproquedeBparfest l"ensemblef -1(B) =x∈E|f(x)∈BEF f -1(B)Bf xy B f -1(B)Remarque. Ces notions sont plus difficiles à maîtriser qu"il n"y paraît! f(A)est un sous-ensemble deF,f-1(B)est un sous-ensemble deE.La notation "f-1(B)» est un tout, rien ne dit quefest un fonction bijective (voir plus loin). L"image réciproque
existe quelque soit la fonction.L"image directe d"un singletonf({x}) =f(x)est un singleton. Par contre l"image réciproque d"un singleton
f-1{y}dépend def. Cela peut être un singleton, un ensemble à plusieurs éléments; mais cela peut-êtreEtout
entier (sifest une fonction constante) ou même l"ensemble vide (si aucune image parfne vauty).2.3. Antécédents
Fixonsy∈F. Tout élémentx∈Etel quef(x) =yest unantécédentdey. En termes d"image réciproque l"ensemble des antécédents deyestf-1({y}). Sur les dessins suivants, l"élémentyadmet 3 antécédents parf. Ce sontx1,x2,x3.EFf yx 1x 2x 3xy x 1x 2x 3yMini-exercices.
1. P ourdeux applications f,g:E→F, quelle est la négation def=g? 2. R eprésenterle graphe de f:N→Rdéfinie parn7→4n+1. 3.Soient f,g,h:R→Rdéfinies parf(x) =x2,g(x) =2x+1,h(x) =x3-1. Calculerf◦(g◦h)et(f◦g)◦h.
4.Pour la fonctionf:R→Rdéfinie parx7→x2représenter et calculer les ensembles suivants :f([0,1[),f(R),
ENSEMBLES ET APPLICATIONS3. INJECTION,SURJECTION,BIJECTION73. Injection, surjection, bijection
3.1. Injection, surjection
SoitE,Fdeux ensembles etf:E→Fune application.Définition 3.festinjectivesi pour toutx,x′∈Eavecf(x) =f(x′)alorsx=x′. Autrement dit :∀x,x′∈Ef(x) =f(x′) =⇒x=x′Définition 4.
festsurjectivesi pour touty∈F, il existex∈Etel quey=f(x). Autrement dit :∀y∈F∃x∈Ey=f(x)Une autre formulation :fest surjective si et seulement sif(E) =F.
Les applicationsfreprésentées sont injectives :EFf xy EF) Les applicationsfreprésentées sont surjectives :EFf xy EFRemarque.Encore une fois ce sont des notions difficiles à appréhender. Une autre façon de formuler l"injectivité et la surjectivité
est d"utiliser les antécédents.fest injective si et seulement si tout élémentydeFaau plusun antécédent (et éventuellement aucun).
fest surjective si et seulement si tout élémentydeFaau moinsun antécédent.Remarque.
Voici deux fonctions non injectives :EFf
yxx ′xy xx ′y ENSEMBLES ET APPLICATIONS3. INJECTION,SURJECTION,BIJECTION8Ainsi que deux fonctions non surjectives :EFf
xy EF )yExemple 3.
1.Soitf1:N→Qdéfinie parf1(x) =11+x. Montrons quef1est injective : soitx,x′∈Ntels quef1(x) =f1(x′). Alors
11+x=11+x′, donc 1+x=1+x′et doncx=x′. Ainsif1est injective.
Par contref1n"est pas surjective. Il s"agit de trouver un élémentyqui n"a pas d"antécédent parf1. Ici il est facile
de voir que l"on a toujoursf1(x)⩽1et donc par exempley=2n"a pas d"antécédent. Ainsif1n"est pas surjective.
2.Soitf2:Z→Ndéfinie parf2(x) =x2. Alorsf2n"est pas injective. En effet on peut trouver deux élémentsx,x′∈Z
différents tels quef2(x) =f2(x′). Il suffit de prendre par exemplex=2,x′=-2. f 2n"est pas non plus surjective, en effet il existe des élémentsy∈Nqui n"ont aucun antécédent. Par exemple
y=3: siy=3avait un antécédentxparf2, nous aurionsf2(x) =y, c"est-à-direx2=3, d"oùx=±p3. Mais
alorsxn"est pas un entier deZ. Doncy=3 n"a pas d"antécédent etf2n"est pas surjective.3.2. BijectionDéfinition 5.
festbijectivesi elle injective et surjective. Cela équivaut à : pour touty∈Fil existe un uniquex∈Etel que
y=f(x). Autrement dit :∀y∈F∃!x∈Ey=f(x)L"existence duxvient de la surjectivité et l"unicité de l"injectivité. Autrement dit, tout élément deFa un unique
antécédent parf.EFf xy EFProposition 1.
Soit E,F des ensembles et f:E→F une application. 1.L"applicationfest bijective si et seulement si il existe une applicationg:F→Etelle quef◦g=idFetg◦f=idE.
2.Sifest bijective alors l"applicationgest unique et elle aussi est bijective. L"applicationgs"appelle labijection
réciproquede f et est notée f-1. De plusf-1-1=f .Remarque. f◦g=idFse reformule ainsi ∀y∈F fg(y)=y.Alors queg◦f=idEs"écrit :
∀x∈E gf(x)=x.ENSEMBLES ET APPLICATIONS4. ENSEMBLES FINIS9
Par exemplef:R→]0,+∞[définie parf(x) =exp(x)est bijective, sa bijection réciproque estg:]0,+∞[→R
définie parg(y) =ln(y). Nous avons bienexpln(y)=y, pour touty∈]0,+∞[etlnexp(x)=x, pour tout
x∈R.Démonstration.
1.Sens⇒. Supposonsfbijective. Nous allons construire une applicationg:F→E. Commefest surjective
alors pour chaquey∈F, il existe unx∈Etel quey=f(x)et on poseg(y) =x. On afg(y)=f(x) =y,ceci pour touty∈Fet doncf◦g=idF. On compose à droite avecfdoncf◦g◦f=idF◦f. Alors pour tout
x∈Eon afg◦f(x)=f(x)orfest injective et doncg◦f(x) =x. Ainsig◦f=idE. Bilan :f◦g=idFet
g◦f=idE. Sens⇐. Supposons quegexiste et montrons quefest bijective. -fest surjective : en effet soity∈Falors on notex=g(y)∈E; on a bien :f(x) =fg(y)=f◦g(y) =
idF(y) =y, doncfest bien surjective. -festinjective : soientx,x′∈Etels quef(x) =f(x′). On compose parg(à gauche) alorsg◦f(x) =g◦f(x′)
donc idE(x) =idE(x′)doncx=x′;fest bien injective. 2.Sifest bijective alorsgest aussi bijective carg◦f=idEetf◦g=idFet on applique ce que l"on vient de
démontrer avecgà la place def. Ainsig-1=f.Sifest bijective,gest unique : en effet soith:F→Eune autre application telle queh◦f=idEetf◦h=idF;
en particulierf◦h=idF=f◦g, donc pour touty∈F,fh(y)=fg(y)orfest injective alorsh(y) =g(y),
ceci pour touty∈F; d"oùh=g.Proposition 2.Soientf:E→Fetg:F→Gdes applications bijectives. L"applicationg◦fest bijective et sa bijection réciproque est(g◦f)-1=f-1◦g-1Démonstration.
D"après la proposition
1 , il existeu:F→Etel queu◦f=idEetf◦u=idF. Il existe aussiv:G→Ftel quev◦g=idFetg◦v=idG. On a alors(g◦f)◦(u◦v) =g◦(f◦u)◦v=g◦idF◦v=g◦v=idE. Et
(u◦v)◦(g◦f) =u◦(v◦g)◦f=u◦idF◦f=u◦f=idE. Doncg◦fest bijective et son inverse estu◦v. Commeu
est la bijection réciproque defetvcelle degalors :u◦v=f-1◦g-1.Mini-exercices. 1. Les fonctions suivantes sont-elles injectives, surjectives, bijectives ? f1:R→[0,+∞[,x7→x2. f3:N→N,x7→x2. f4:Z→Z,x7→x-7. f5:R→[0,+∞[,x7→ |x|. 2.Montrer que la fonctionf:]1,+∞[→]0,+∞[définie parf(x) =1x-1est bijective. Calculer sa bijection
réciproque.4. Ensembles finis4.1. CardinalDéfinition 6.
Un ensembleEestfinis"il existe un entiern∈Net une bijection deEvers{1,2,...,n}. Cet entiernest unique et
s"appelle lecardinaldeE(ou lenombre d"éléments) et est noté CardE.Quelques exemples :1.E={rouge,noir}est en bijection avec{1,2}et donc est de cardinal 2.
ENSEMBLES ET APPLICATIONS4. ENSEMBLES FINIS10
2.Nn"est pas un ensemble fini.
3. P ardéfinition le cardinal de l"ensemble vide est 0.Enfin quelques propriétés :
1. Si Aest un ensemble fini etB⊂AalorsBest aussi un ensemble fini et CardB⩽CardA. 2.Si A,Bsont des ensembles finis disjoints (c"est-à-direA∩B=∅) alors Card(A∪B) =CardA+CardB.
3.SiAest un ensemble fini etB⊂AalorsCard(A\B) =CardA-CardB. En particulier siB⊂AetCardA=CardB
alorsA=B. 4.Enfin pour A,Bdeux ensembles finis quelconques :Card(A∪B) =CardA+CardB-Card(A∩B)Voici une situation où s"applique la dernière propriété :
BA La preuve de la dernière propriété utilise la décompositionA∪B=A∪B\(A∩B)
Les ensemblesAetB\(A∩B)sont disjoints, donc
Card(A∪B) =CardA+CardB\(A∩B)=CardA+CardB-Card(A∩B) par la propriété 2, puis la propriété 3.4.2. Injection, surjection, bijection et ensembles finisProposition 3.
Soit E,F deux ensembles finis et f:E→F une application. 1.Si f est injective alors CardE⩽CardF.
2.Si f est surjective alors CardE⩾CardF.
3. Si f est bijective alors CardE=CardF.Démonstration. 1.Supposonsfinjective. NotonsF′=f(E)⊂Falors la restrictionf|:E→F′(définie parf|(x) =f(x)) est une
bijection. Donc pour chaquey∈F′est associé un uniquex∈Etel quey=f(x). DoncEetF′ont le même
nombre d"éléments. Donc CardF′=CardE. OrF′⊂F, ainsi CardE=CardF′⩽CardF.
2.Supposonsfsurjective. Pour tout élémenty∈F, il existe au moins un élémentxdeEtel quey=f(x)et donc
CardE⩾CardF.
3.Cela découle de (
1 ) et ( 2 ) (ou aussi de la preuve du ( 1 )).Proposition 4. Soit E,F deux ensembles finis et f:E→F une application. SiCardE=CardF
alors les assertions suivantes sont équivalentes : i. f est injective, ii. f est surjective, iii. f est bijective.ENSEMBLES ET APPLICATIONS4. ENSEMBLES FINIS11
Démonstration.Le schéma de la preuve est le suivant : nous allons montrer successivement les implications :
(i) =⇒(ii) =⇒(iii) =⇒(i) ce qui prouvera bien toutes les équivalences.(i) =⇒(ii). Supposonsfinjective. AlorsCardf(E) =CardE=CardF. Ainsif(E)est un sous-ensemble deF
ayant le même cardinal queF; cela entraînef(E) =Fet doncfest surjective.(ii) =⇒(iii). Supposonsfsurjective. Pour montrer quefest bijective, il reste à montrer quefest injective.
Raisonnons par l"absurde et supposonsfnon injective. AlorsCardf(E) la même image). Orf(E) =Fcarfsurjective, doncCardF (iii) =⇒(i). C"est clair : une fonction bijective est en particulier injective.Appliquez ceci pour montrer leprincipe des tiroirs:Proposition 5. Si l"on range dansktiroirs,n>kpaires de chaussettes alors il existe (au moins) un tiroir contenant (au moins) deux Malgré sa formulation amusante, c"est une proposition souvent utile. Exemple : dans un amphi de400étudiants, il y a En particulier le nombre d"applications deEdans lui-même estnn. Par exemple siE={1,2,3,4,5}alors ce nombre suivante : le nombre d"applications d"un ensemble ànéléments vers un ensemble àpéléments estpn. Initialisation.Pourn=1, une application deEdansFest définie par l"image de l"unique élément deE. Il y a Hérédité.Fixonsn⩾1et supposons quePnest vraie. SoitEun ensemble àn+1éléments. On choisit et fixe a∈E; soit alorsE′=E\{a}qui a biennéléments. Le nombre d"applications deE′versFestpn, par l"hypothèse de récurrence(Pn). Pour chaque applicationf:E′→Fon peut la prolonger en une applicationf:E→Fen choisissant l"image dea. On apchoix pour l"image deaet doncpn×pchoix pour les applications deEversF. l"image dea2il restep-1choix (cara2ne doit pas avoir la même image quea1). Pour l"image dea3il y ap-2 possibilités. Ainsi de suite : pour l"image deakil y ap-(k-1)choix... Il y a au finalp×(p-1)×···×(p-(n-1)) applications injectives.Notationfactorielle:n!=1×2×3×···×n. Avec 1!=1 et par convention 0!=1. Démonstration.Nous allons le prouver par récurrence surn. Soit(Pn)l"assertion suivante : le nombre de bijections P1est vraie. Il n"y a qu"une bijection d"un ensemble à 1 élément dans un ensemble à 1 élément. Fixonsn⩾1et supposons quePnest vraie. SoitEun ensemble àn+1éléments. On fixea∈E. Pour chaque b∈Eil y a -par l"hypothèse de récurrence- exactementn!applications bijectives deE\{a} →E\{b}. Chaque application se prolonge en une bijection deE→Fen posanta7→b. Comme il y an+1choix deb∈Ealors nous Supposons que la proposition soit vraie pourn⩾1fixé. SoitEun ensemble àn+1éléments. On fixea∈E. Il y a les sous-ensemblesAqui ne contiennent pasa: ce sont les sous-ensemblesA⊂E\ {a}. Par l"hypothèse de les sous-ensemblesAqui contiennenta: ils sont de la formeA={a}∪A′avecA′⊂E\{a}. Par l"hypothèse de Par le principe de récurrence, nous avons prouvé que si CardE=nalors on a CardP(E) =2n.4.5. Coefficients du binôme de Newton4.3. Nombres d"applications
SoientE,Fdes ensembles finis, non vides. On note CardE=net CardF=p.Proposition 6. Le nombre d"applications différentes de E dans F est :p nAutrement dit c"est(CardF)CardE. Exemple 4.
Démonstration.
FixonsFetp=CardF. Nous allons effectuer une récurrence surn=CardE. Soit(Pn)l"assertion AinsiPn+1est vérifiée.
Conclusion.Par le principe de récurrencePnest vraie, pour toutn⩾1.Proposition 7. Le nombre d"injections de E dans F est :
SupposonsE={a1,a2,...,an}; pour l"image dea1nous avonspchoix. Une fois ce choix fait, pour SoitEun ensemble fini de cardinaln.Proposition 9.
Il y a2CardEsous-ensembles de E :CardP(E) =2nExemple 6. SiE={1,2,3,4,5}alorsP(E)a 25=32 parties. C"est un bon exercice de les énumérer : l"ensemble vide :∅, 5 singletons :{1},{2},...,
10 paires :{1,2},{1,3},...,{2,3},...,
10 triplets :{1,2,3},...,
5 ensembles à 4 éléments :{1,2,3,4},{1,2,3,5},...,
etEtout entier :{1,2,3,4,5}. Démonstration.Encore une récurrence surn=CardE. Sin=1,E={a}est un singleton, les deux sous-ensembles sont :∅etE. Le bilan : 2
n+2n=2n+1partiesA⊂E. Définition 7.
Le nombre de parties àkéléments d"un ensemble ànéléments est notén kouCk n. ENSEMBLES ET APPLICATIONS4. ENSEMBLES FINIS13
Exemple 7.Les parties à deux éléments de{1,2,3}sont{1,2},{1,3}et{2,3}et donc3 2=3. Nous avons déjà classé les parties
de{1,2,3,4,5}par nombre d"éléments et donc 5 0=1 (la seule partie n"ayant aucun élément est l"ensemble vide),
5 1=5 (il y a 5 singletons),
5 2=10 (il y a 10 paires),
5 3=10, 5quotesdbs_dbs45.pdfusesText_45
[PDF] a inclus dans b implique f(a) inclus dans f(b)
[PDF] combien f possède-t-il de sous ensembles ?
[PDF] padlet français
[PDF] paralangage exemple
[PDF] type de paralangage
[PDF] communication non verbale cours
[PDF] paralangage communication non verbale
[PDF] paralangage exercice
[PDF] le silence dans la communication non verbale
[PDF] le paralangage signifie communiquer sans parler
[PDF] définition élève en difficulté scolaire
[PDF] concept de souffrance
[PDF] concept douleur
[PDF] conflit latent définition
