 Chapitre 1. Ensembles et applications.
Chapitre 1. Ensembles et applications.
18 févr. 2013 Soit f : A −→ B une application. Le sous-ensemble. {(xf (x))
 Chapitre 2 Ensembles et sous-ensembles
Chapitre 2 Ensembles et sous-ensembles
Ensembles et sous-ensembles. 1. Notion d'ensemble - Elément d'un ensemble. Dans une théorie mathématique il est rare qu'un objet intervienne seul ; d'o`u l
 Cours de mathématiques - Exo7
Cours de mathématiques - Exo7
Nous avons déjà vu que ceci est un espace vectoriel. Mini-exercices. Parmi les ensembles suivants reconnaître ceux qui sont des sous-espaces vectoriels : 1. (x
 COMBINATOIRE ET DÉNOMBREMENT
COMBINATOIRE ET DÉNOMBREMENT
×2 ( facteurs) possibilités d'obtenir un sous-ensemble de soit 2 . Exemple www.maths-et-tiques.fr/index.php/mentions-legales.
 Cours : Ensembles et applications
Cours : Ensembles et applications
les mathématiques sur des bases logiques. Il reçut une lettre d'un tout jeune cl(x) est donc un sous-ensemble de E on le note aussi x. Si y ∈ cl(x)
 [PDF] Groupes - Exo7 - Cours de mathématiques
[PDF] Groupes - Exo7 - Cours de mathématiques
4. Montrer que l'ensemble des matrices 2×2 de déterminant 1 ayant leurs coefficients dans Z est un sous-groupe de (Gl2×)
 Analyse combinatoire
Analyse combinatoire
6 mars 2008 Mathématiques Générales B. Université de Gen`eve. Sylvain Sardy. 6 mars ... – Combien y a-t-il de sous-ensembles d'un ensemble de cardinalité n?
 THÉORIE DES ENSEMBLES
THÉORIE DES ENSEMBLES
Soit Ω l'ensemble des nombres possibles d'obtenir de la somme de deux dés. Ω. 2
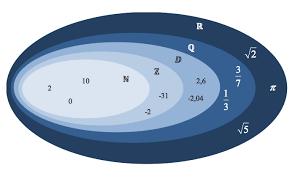 ENSEMBLES DE NOMBRES
ENSEMBLES DE NOMBRES
sous forme d'un intervalle : 2xГ3<4. 0 1. 0 1. 0 1. 0 1. 0 1. 0 1. 0 1. 0 1. Page 5. 5 sur 8. Yvan Monka – Académie de Strasbourg – www.maths-et-tiques.fr. 2xГ3 ...
 Chapitre 1 Ensembles et sous-ensembles
Chapitre 1 Ensembles et sous-ensembles
2?) Soit E un ensemble qui est la réunion de deux sous-ensembles on s'efforce souvent de les écrire en utilisant des symboles mathématiques.
 ENSEMBLES DE NOMBRES
ENSEMBLES DE NOMBRES
Un nombre rationnel peut s'écrire sous la forme d'un quotient a b avec a un entier et b un entier non nul. L'ensemble des nombres rationnels est noté ?.
 Cours : Ensembles et applications
Cours : Ensembles et applications
les mathématiques sur des bases logiques. Il reçut une lettre d'un tout jeune mathématicien : « J'ai bien lu votre premier.
 Cours de mathématiques - Exo7
Cours de mathématiques - Exo7
Sous-groupes. Montrer qu'un ensemble est un groupe à partir de la définition peut être assez long. Il existe une autre technique c'est de montrer qu'un
 Cours de mathématiques - Exo7
Cours de mathématiques - Exo7
L'ensemble F1 = (x y) ? 2
 Chapitre 1. Ensembles et applications.
Chapitre 1. Ensembles et applications.
18 févr. 2013 Soit f : A ?? B une application. Le sous-ensemble. {(xf (x))
 COMBINATOIRE ET DÉNOMBREMENT
COMBINATOIRE ET DÉNOMBREMENT
Alors est l'ensemble des couples possibles pour deux dés. On a par exemple : Page 3. Yvan Monka – Académie de Strasbourg – www.maths-et
 Chapitre 1 Ensembles et sous-ensembles
Chapitre 1 Ensembles et sous-ensembles
Ensembles et sous-ensembles. 1. Notion d'ensemble - Elément d'un ensemble. Un ensemble est une collection d'objets satisfaisant un certain nombre de
 Analyse combinatoire
Analyse combinatoire
6 mars 2008 Mathématiques Générales B. Université de Gen`eve ... distincts est un sous-ensemble `a k éléments de cet ensemble. Les éléments sont.
 Chapitre 2 Ensembles et sous-ensembles
Chapitre 2 Ensembles et sous-ensembles
Ensembles et sous-ensembles. 1. Notion d'ensemble - Elément d'un ensemble. Dans une théorie mathématique il est rare qu'un objet intervienne seul ; d'o`u
 [PDF] Chapitre 1 Ensembles et applications
[PDF] Chapitre 1 Ensembles et applications
18 fév 2013 · Pour un ensemble A l'ensemble de tous les sous-ensembles de A est noté 2A ou P(A) Exemple Soit A = {01} Les sous-ensembles de A sont ? A
 [PDF] Chapitre 1 Ensembles et sous-ensembles - Université de Rennes
[PDF] Chapitre 1 Ensembles et sous-ensembles - Université de Rennes
Définition 1 3 – Soient A et B deux sous-ensembles d'un ensemble E L'ensemble {x x ? A et x ? B} est appelé l'intersection des ensembles A
 [PDF] ensemblepdf
[PDF] ensemblepdf
Un ensemble est une collection d'objets satisfaisant un certain nombre de propriétés et chacun de ces objets est appelé élément de cet ensemble
 [PDF] THÉORIE DES ENSEMBLES
[PDF] THÉORIE DES ENSEMBLES
L'ensemble est dit un sous-ensemble de si et seulement si tous les éléments de sont aussi des éléments de On dit alors que l'ensemble est inclus dans l'
 [PDF] 1 Ensembles - Apprendre-en-lignenet
[PDF] 1 Ensembles - Apprendre-en-lignenet
Un sous-ensemble est un ensemble dont chaque élément est aussi contenu dans un autre ensemble Si A est un sous-ensemble de B on note A?B Par exemple si J
 [PDF] ENSEMBLES DE NOMBRES - maths et tiques
[PDF] ENSEMBLES DE NOMBRES - maths et tiques
Un nombre rationnel peut s'écrire sous la forme d'un quotient a b avec a un entier et b un entier non nul L'ensemble des nombres rationnels est noté ?
 [PDF] Généralités sur les ensembles - livres-mathematiquesfr
[PDF] Généralités sur les ensembles - livres-mathematiquesfr
Un des probl`emes qui nous intéressera rapidement est de déterminer tous les sous-ensembles d'un ensemble fini donné Pour cela nous avons besoin d'un ensemble
 [PDF] Introduction à la notion densembles - Université de Toulouse
[PDF] Introduction à la notion densembles - Université de Toulouse
Un ensemble est une collection d'objets deux à deux distincts appelés éléments On peut définir un ensemble de deux manières : en extension : on donne la liste
 [PDF] Ensembles et applications - Exo7 - Cours de mathématiques
[PDF] Ensembles et applications - Exo7 - Cours de mathématiques
que E est un sous-ensemble de F ou une partie de F • L'égalité E = F si et seulement si E ? F et F ? E • Ensemble des parties de E On note
 [PDF] Théorie des ensembles
[PDF] Théorie des ensembles
que pour tout ? ? E ? soit un sous-ensemble de E Voici un exemple : mathématique sur des ensembles qui s'exprime en quantifiant les variables et les
C'est quoi un sous-ensemble en maths ?
Étant donné un ensemble E; un sous-ensemble de E est un ensemble dont tous les éléments appartiennent à l'ensemble E. Synonyme de partie d'un ensemble. Un sous-ensemble propre ou strict d'un ensemble E est un sous-ensemble de E qui n'est pas égal à E.Quels sont les sous-ensembles ?
Un sous-ensemble est aussi un ensemble. Soient deux ensembles A et B. On dit que B est un sous-ensemble de A si tous les éléments de B sont aussi éléments de A. Exemple : L'ensemble B des entiers naturels de 1 à 3 est un sous-ensemble de l'ensemble A constitué par les entiers naturels de 1 à 7.Comment montrer qu'un ensemble est un sous-ensemble ?
Pour démontrer que F est un sous-espace vectoriel de E , on applique la caractérisation des sous-espaces vectoriels, c'est-à-dire qu'on vérifie que 0E?F 0 E ? F et que, pour tout couple (x,y)?F2 ( x , y ) ? F 2 et tout scalaire ??K ? ? K , on a {x+y?F?x?F.- On dit que A est inclus dans B si chaque élément de A est un élément de B. On note A ? B. On dit aussi “A est contenu dans B” ou “A est une partie de B” ou “A est un sous-ensemble de B”. Remarques - • A ? A • Si A ? B et B ? C, alors A ? C • A = B si et seulement si (A ? B et B ? A).
Chapitre 1
Ensembles et sous-ensembles
1. Notion d"ensemble - El´ement d"un ensemble
Unensembleest une collection d"objets satisfaisant un certain nombrede propri´et´es et chacun de ces objets est appel´e´el´ementde cet ensemble. Si xest un ´el´ement de l"ensembleE, on dit aussi quexappartient `aEet on notex?E. Sixn"appartient pas `aE, on notex??E. Deux ensembles sont´egauxs"ils ont les mˆemes ´el´ements.On admet l"existence d"un ensemble n"ayant aucun ´el´ement. Cet ensemble est appel´eensemble videet not´e∅.Notations
Il y a des notations r´eserv´ees pour certains ensembles ; par exemple,N est l"ensemble des entiers naturels ;Z,Q,RetCd´esignent respectivement l"ensemble des entiers relatifs, des nombres rationnels, des nombres r´eels et des nombres complexes ;R?,R+,R?+d´esignent les r´eels non nuls, les r´eels positifs, les r´eels strictement positifs, etc. L"ensembleEdont les ´el´ements sont 1, 2, 3, 4 est not´eE={1,2,3,4}. Un ensemble `a un seul ´el´ementxest not´e{x}et on l"appelle lesingleton {x}. On a doncx? {x}(et pasx={x}). Plus g´en´eralement, soitEun ensemble etP(x) une propri´et´e v´erifi´ee ou non suivant la valeur dex, ´el´ement de E ; l"ensembleAdont les ´el´ements sont les ´el´ementsxdeEqui v´erifientP(x) est not´eA={x|x?EetP(x)}ouA={x?E|P(x)}.
2. Relation d"inclusion
D´efinition 1.1 -SoientAetBdeux ensembles. On dit queAest inclus dansBsi chaque ´el´ement deAest un ´el´ement deB.On noteA?B. On dit aussi "Aest contenu dansB" ou "Aest une partie deB" ou "Aest un sous-ensemble deB". AB A?BIntersection et r´eunion
Remarques -A?A
SiA?BetB?C, alorsA?C
A=Bsi et seulement si (A?BetB?A).
On traduit les propri´et´es pr´ec´edentes en disant que la relation d"inclusion est respectivementr´eflexive,transitiveetantisym´etrique. On peut rapprocher a=b. De telles relations sont appel´eesrelations d"ordre.Exemples -N?Z?Q
{x?R|0< x <4} ?R+
D´efinition 1.2 -Soit E un ensemble. Les sous-ensembles de E forment un ensemble appel´eensemble des parties de Eet not´eP(E). Exemple -SiE={1,2}, alorsP(E) ={∅,{1},{2},E}. Remarque -Les trois assertionsx?E,{x} ?Eet{x} ? P(E) sont´equivalentes.
Exercice -1◦) SoitE={1,2,3}. Donner tous les sous-ensembles deE. 2 ◦) Montrer, par r´ecurrence surn, qu"un ensemble `an´el´ements a 2 nsous-ensembles. 3 ◦) SoientAetBdes sous-ensembles d"un ensembleE.Montrer que (A?Bsi et seulement siP(A)? P(B)).
3. Intersection et r´eunion
D´efinition 1.3 -Soient A et B deux sous-ensembles d"un ensembleE. L"ensemble{x|x?Aetx?B}est appel´e l"intersection des ensemblesA etBet est not´eA∩B. SiA∩B=∅, on dit queAetBsont disjoints. L"ensemble{x|x?Aoux?B}est appel´e l"union des ensemblesAetBet est not´eA?B. BAA∩B={x|x?Aetx?B}
BAA?B={x|x?Aoux?B}
- 2 -ENSEMBLES ET SOUS-ENSEMBLES
SoientAetBdeux sous-ensembles d"un ensembleE. On a :1)A∩ ∅=∅etA? ∅=A
2)A∩B?AetA∩B?B
3)A?A?BetB?A?B
4)A?B=Asi et seulement siB?A
5)A∩B=Asi et seulement siA?B
Propri´et´es de∩et?-
Soient A, B, C trois sous-ensembles d"un ensembleE. On a :1)A?B=B?A
2)A∩B=B∩A
3)A?(B?C) = (A?B)?C
4)A∩(B∩C) = (A∩B)∩C
5)A?(B∩C) = (A?B)∩(A?C)
6)A∩(B?C) = (A∩B)?(A∩C)
On traduit ces propri´et´es en disant que?et∩sontcommutatives(propri´et´es1 et 2),associatives(propri´et´es 3 et 4), que?estdistributive par rapport `a∩
(propri´et´e 5) et∩estdistributive par rapport `a?(propri´et´e 6). Ces propri´et´es
seront ´etudi´ees dans le chapitre sur les lois de composition internes. Pour s"en souvenir, on peut les comparer aux propri´et´es analogues de l"addition et de la mutiplication dansR: poura,b,cr´eels, on aa+b=b+a, ab=ba, a+(b+c) = (a+b)+c, a(bc) = (ab)c, a(b+c) =ab+ac. Mais on n"a pas l"´equivalent de la propri´et´e 5 ; en g´en´eral, on n"a pasa+(bc) =ab+ac(trouver un exemple). !Ne pas oublier les parenth`eses. Par exemple,A∩B?Cn"a pas de sens. SiA= [0,1],B= [1,2] etC= [2,+∞[, on a (A∩B)?C={1}?[2,+∞[, etA∩(B?C) ={1}. G´en´eralisation -SiA1,A2,...,Ansont des sous-ensembles d"un ensemble E, on d´efinit de mˆeme la r´eunionA1?A2?...?Ancomme l"ensemble desxqui appartiennent `a au moins l"un des ensemblesA1,A2,...ouAnet l"intersectionA1∩A2∩...∩Ancomme l"ensemble desxqui appartiennent `a tous les ensemblesA1,A2,...,An: A1?A2?...?An={x|?i? {1,2,...,n}, x?Ai}
A1∩A2∩...∩An={x|?i? {1,2,...,n}, x?Ai}
Exercice -1◦) SoientA,B,C,Ddes sous-ensembles d"un ensembleE. Mon- trer que(A?B)∩(C?D) = (A∩C)?(A∩D)?(B∩C)?(B∩D).Simplifier le r´esultat lorsque l"on aA?C.
2 ◦) SoitEun ensemble qui est la r´eunion de deux sous-ensembles AetB. On suppose queAetBsont finis et ont respectivementnet m´el´ements. SiAetBsont disjoints, combienEa-t-il d"´el´ements ? - 3 -Compl´ementaire d"un ensemble
Plus g´en´eralement, siA∩Bap´el´ements, montrer queEen a n+m-p.4. Compl´ementaire d"un ensemble
D´efinition 1.4 -SoientEun
ensemble etAun sous-ensemble deE. Le compl´ementaire deA dansEest l"ensemble {x|x?Eetx??A}. On le note?EAouE\Aou encore lorsqu"il n"y a pas d"ambigu¨ıt´e sur E, cA,Acou A. AE ?EA={x?E;x??A} Propri´et´es du compl´ementaire (Lois de De Morgan) -SoientEun ensemble,AetBdes sous-ensembles deE.
1)?E(?EA) =A
2)A?Bsi et seulement si (?EB)?(?EA)
3)?E(A?B) = (?EA)∩(?EB)
4)?E(A∩B) = (?EA)?(?EB)
D´efinition 1.5 -SoientAetBdeux sous-ensembles d"un ensembleE. On note1 -A\Bl"ensemble{x?A|x /?B}et on l"appelle diff´erence deAetB.
2 -AΔBl"ensemble (A?B)\(A∩B) et on l"appelle diff´erence sym´etrique
deAetB.Proposition 1.6 -AΔB= (A\B)?(B\A).
BAA\B={x?A;x??B}
BAAΔB= (A?B)\(A∩B)
Remarques -La diff´erence sym´etrique correspond au "ou" exclusif :AΔB est l"ensemble des points qui appartiennent `aAou `aB, maisPAS `aAetBen mˆeme temps.
Lorsque l"on aB?A, la diff´erence deAetBest aussi le compl´ementaire deBdansA.A\B=A∩Bc.
A?Bsi et seulement siA\B=∅.
- 4 -ENSEMBLES ET SOUS-ENSEMBLES
!Ne pas oublier les parenth`eses.Trouver un exemple d"ensembles v´erifiant (A\B)\C?=A\(B\C). Exercice -1◦) SoientA={x?R|x2-3x+ 1>0}etB={x?R|x >0}. Montrer que les ensemblesAc,Bc,A∩B,A?B,A\B,B\Aet AΔBsont des intervalles ou des r´eunions d"intervalles et pr´eciser lesquels. 2 ◦) SoientAetBdes sous-ensembles d"un ensembleE. Montrer que les trois propri´et´es suivantes sont ´equivalentes :1)A=B2)A\B=B\A3)AΔB=∅
3 ◦) Mˆeme question pour les six propri´et´es suivantes. (On peut montrer qu"elles sont toutes ´equivalentes `a la premi`ere) :1)A?B2)Bc?Ac3)A∩B=A
4)A?B=B5)A\B=∅6)AΔB=B\A
5. Partitions
D´efinition 1.7 -SoientEun ensemble etA1,A2,...,Andes sous-ensembles deE. On dit que ces sous-ensembles forment une partition deEsi les trois conditions suivantes sont v´erifi´ees :1) Leur r´eunion est ´egale `aE:E=A1?A2?...?An
2) Ils sont deux `a deux disjoints : sii,j? {1,2,...,n}eti?=jalors
A i∩Aj=∅3) Chacun de ces ensembles est non vide : pour touti? {1,2,...,n}, Ai?=∅.
A1A2A3A4
Sur le dessin ci-dessus, les ensemblesA1,...,A4forment une partition de l"ensembleE. Exemples -SoientE=N, A1le sous-ensemble form´e des entiers pairs, A2le sous-ensemble form´e des entiers impairs. Alors, les sous-
ensemblesA1etA2forment une partition deE.SoientE=R, A1=R?+, A2=R?-, A3={0}. Alors, les
sous-ensemblesA1,A2etA3forment une partition deE. !Attention `a ne pas confondre les termes "disjoint" et "distinct."R- etR+sont distincts, mais pas disjoints.R-?etR+?sont distincts et disjoints. - 5 -Produit
Exercice -Soienta,betcdes r´eels, aveca≥0. A quelle condition les sous- ensembles]0,a[,]- ∞,b]et[c,+∞[forment-ils une partition de R?6. Produit
D´efinition 1.8 -- SoientEetFdeux ensembles,xun ´el´ement deEet yun ´el´ement deF. Le couple (x,y) est la donn´ee des deux ´el´ementsxet ydans cet ordre. Les ´el´ementsxetysont appel´es respectivement premi`ere et deuxi`eme coordonn´ee du couple (x,y). Deux couples (x,y) et (x?,y?) sont ´egaux si et seulement si on a (x=x?ety=y?). Le produit cart´esienE×F est l"ensemble des couples (x,y) o`ux?Eety?F. Exemples -SiE=F=R, le produitR×Rest aussi not´eR2. On le repr´esente souvent par l"ensemble des points du plan affine euclidien, en choisissant un rep`ere orthonorm´e (O,e1,e2). Le couple (x,y) est repr´esent´e par le point d"abscissexet d"ordonn´eey. SiA= [2,5] etB= [2,4], le produitA×Best un sous- ensemble deR2qui peut ˆetre repr´esent´e par le rectangle sur la figure ci-dessous.A×B
OB A e1 e 2242 5 Remarques -Il ne faut pas confondre le couple (x,y) et l"ensemble{x,y}. Six?=y, on a (x,y)?= (y,x), mais{x,y}={y,x}. Le couple (x,x) est repr´esent´e par un point de la premi`ere diagonale et l"ensemble{x,x}est le singleton{x}.
A?EetB?Fsi et seulement siA×B?E×F.
Un produit cart´esien de deux ensembles est vide si et seulement si l"un au moins des deux ensembles est vide. G´en´eralisation -Si on consid`ere des ensemblesE1,E2,...,En, on peut de mˆeme d´efinir les n-uples (x1,x2,...,xn) o`ux1?E1,x2?E2,...,xn?En - 6 -ENSEMBLES ET SOUS-ENSEMBLES
et le produitE1×E2×...×En. En particulier,R×...×R? nfacteursest encore not´e R n. De mˆeme, on noteEnl"ensembleE×...×E? nfacteurs. Exercice -1◦) SoitA=B={1,2}.Donner tous les sous-ensembles deA×B. 2 ◦) On consid`ere les ensemblesE={1,2,3,4},
A={(i,j)?E2|i < j},
B={(i,j)?E2|i=j},
C={(i,j)?E2|i > j}.
Les repr´esenter par un dessin, et montrer queA,BetCforment une partition deE×E. - 7 -EXERCICES D"APPLICATION
Exercice n◦1
EA,?EB,A∩B,A?B,A\B,B\AetAΔB.
Exercice n◦2
SoientA,BetCdes sous-ensembles d"un ensembleE. Les ´egalit´es suivantes sont-elles toujours vraies? (Sinon, donner un contre-exemple)1)A\(B\C) = (A\B)\C
2)A?(B\C) = (A?B)\(A?C)
Exercice n◦3
SoientA,B,CetDdes sous-ensembles d"un ensembleE. Montrer les ´egalit´esA\B= (A?B)\BetAΔB= (A∩Bc)?(Ac∩B).
Exercice n◦4
SoientA,BetCdes sous-ensembles d"un ensembleE.
1)Simplifier (A\C)?(B\C)?(A?B)c?C.
2)Simplifier (A\(Bc?C))?Ac?Bc?C.
Exercice n◦5
SoientA,B,CetDdes sous-ensembles d"un ensembleE.
1)Montrer que l"on a ((A∩B)?Bc=A?Bc) et ((A\B)?B=A?B).
2)En d´eduire que l"on aE= (C\D)?(A∩B∩Cc)?Ac?Bc?D.
Exercice n◦6
L´eon et Nicole travaillent dans un centre de lexicographie. Ils disposent de trois dictionnairesA,BetC. Leur patron donne `a L´eon le travail suivant : former d"abord une liste des mots communs aux dictionnairesAetB, former ensuite une liste de mots communs aux dictionnairesBetC, enfin chercher les mots qui figurent dans l"une ou l"autre liste, mais pas dans les deux `a la fois. L´eon demande `a Nicole de l"aider en dressant une liste des mots figurant dans le dictionnaireAou dans le dictionnaireC, mais pas dans les deux `a la fois. Ensuite L´eon se charge de trouver les mots communs `a cette liste et au dictionnaireB. Le patron obtiendra-t-il le r´esultat demand´e ?Exercice n◦7
SoientEetFdeux ensembles,AetBdeux sous-ensembles deEetCetD deux sous-ensembles deF. Les ´egalit´es suivantes sont-elles toujours vraies?1)(A×C)∩(B×D) = (A∩B)×(C∩D).
- 8 -2)(A×C)\(B×C) = (A\B)×C.
Exercice n◦8
SoientEetFdeux ensembles. Un sous-ensembleXdeE×Fest-il toujours de la formeA×Bo`uAappartient `aP(E) etBappartient `aP(F) ?Exercice n◦9
On suppose que les sous-ensemblesA1,A2,A3etA4forment une partition de l"ensembleE. Combien y-a-t-il de fa¸cons de former une partition deE avec des sous-ensembles qui sont des r´eunions de certains desAi?INDICATIONS ET SOLUTIONS SOMMAIRES
Exercice n◦2
1)Non - Contre-exemple :A=C=R,B=∅,A\(B\C) =R,(A\B)\C=∅.
2)Non - Contre-exemple :A=R,B=C=∅,A?(B\C) =R,(A?B)\
(A?C) =∅.Exercice n◦4
On trouveE.
Exercice n◦6
Oui - Consid´ererA,B,Ccomme des ensembles (de mots) et utiliser la distributivit´e de∩par rapport `a Δ.Exercice n◦7
Oui.Exercice n◦8
Non - Contre-exemple :E=F=RetX={(x,y)?R2|x2+y2= 1}.Exercice n◦9
15. - 9 -Chapitre 2
El´ements pour comprendre un ´enonc´e
Ce chapitre est consacr´e `a lacompr´ehensiond"un ´enonc´e. Pourd´emontrer un ´enonc´e donn´e, il faut se reporter au chapitre suivant. Les tables de v´erit´e donn´ees dans ce chapitre sont utilespour connaitre la valeur d"une proposition (dans quels cas est-elle vraie ou fausse), mais ne servent pas pour d´emontrer une proposition. Un ´enonc´e est parfois difficile `a comprendre. Il peut contenir des mots utilis´es dans un sens diff´erent du sens courant ou des mots sp´ecifiques au langage math´ematique. S"il n"est pas ´ecrit avec assez de soin, il peut devenir ambigu. Pour pr´eciser ou mieux comprendre le sens d"un ´enonc´e ou des mots employ´es, on s"efforce souvent de les ´ecrire en utilisant des symbolesmath´ematiques, deset, desou, des =?, des??, des?ou des?.Exemples -Soitfune application deRdansR.
L"´enonc´e "l"applicationfa un z´ero entre -1 et 1" est ambigu : faut-il comprendre "un et un seul z´ero" ou "au moins un z´ero" ?1 et -1 sont-ils admis? Si on ´ecrit?x?[-1,1], f(x) = 0, ces
ambigu¨ıt´es sont lev´ees. Dire que "la suite (un) converge vers?" peut se traduire par : ?ε?R?+,?N?N,?n?N,(n > N=? |un-?|< ε). L"int´erˆet de ce type d"´ecriture est de pr´eciser la signification d"un ´enonc´e complexe, mais il parait parfois difficile `a d´echiffrer. Il faut ˆetre capable de bien comprendre le sens d"une telle formule, de la traduire en fran¸cais et inversement de traduire sous cette forme un ´enonc´e exprim´e en fran¸cais. L"objet de ce chapitre est de vous donner quelques ´el´ements pour vous aider `a y parvenir.1. Propositions
Confront´e `a un ´enonc´e, un math´ematicien souhaite pouvoir d´ecider dans quelles conditions il est vrai ou faux. Cet ´enonc´e peut contenir une ou plusieurs variables. Nous appelleronspropositionun ´enonc´e math´ematique dont on peut d´ecider s"il est vrai ou faux lorsque toutes lesvariables ont ´et´e remplac´ees par des valeurs connues. Exemples -"2≥1" est une proposition vraie."1=2" est une proposition fausse.
´egal `a 4, elle est vraie et lorsquenest ´egal `a 7, elle est fausse.Propositions
Sixetysont des r´eels, "x2=y" est une proposition. A partir de propositionsPetQdonn´ees, on peut d´efinir de nouvelles propositions (nonP), (PetQ), (PouQ), (P=?Q), (P??Q), dont on connait la valeur de v´erit´e d`es que l"on connait celles dePetQ.1.1. N´egation
D´efinition 2.1 -SoitPune proposition. La n´egation dePest une proposition not´ee (nonP). Elle est vraie lorsquePest fausse et fausse lorsque Pest vraie. On obtient la table de v´erit´e suivante (o`u V estmis pour vraie et F pour fausse) :P(nonP)
VF FV Exemples -Soitxun r´eel. La proposition (non(x= 1)) est not´ee (x?= 1). les mˆemes valeurs de v´erit´e que la proposition (n >2). Exercice -D´eterminer l"ensemble des r´eelsxqui v´erifient la proposition :1.2. Conjonction et disjonction
D´efinition 2.2 -SoientPetQdeux propositions.
1) La conjonction des deux propositionsPetQest une proposition not´ee
(PetQ). Elle est vraie lorsque les deux propositionsPetQsont vraies, et elle est fausse lorsque l"une au moins des deux propositions est fausse.2) La disjonction des deux propositionsPetQest une proposition not´ee
(PouQ). Elle est vraie lorsque l"une au moins des deux propositionsP ouQest vraie et elle est fausse lorsque les deux propositionsPetQsont fausses. On peut r´esumer ce qui pr´ec`ede dans la table suivante :PQ(PetQ)(PouQ)
VVVV VFFV FVFV FFFF - 12 -ELEMENTS POUR COMPRENDRE UN ENONCE
Exemples -Soientnun entier naturel,Pla proposition "nest pair",Q la proposition "nest divisible par 3". Alors lorsquenest ´egal `a 6, (PetQ) est vraie. Lorsquenest ´egal `a 2, 3 ou 6, (PouQ) est vraie.
Soientxun r´eel,Pla proposition (x >1) ,Qla proposition pourx= 0 elle est fausse et quelque soit la valeur dex, la proposition (PouQ) est vraie. !Dans le langage courant, le mot "ou" peut prendre deux sens diff´erents : le sens inclusif qui est celui donn´e plus haut et le sens exclusif, qu"on pr´ecise parfois par "ou bien" : (Pou bienQ) est vraie si l"une des deux propo- sitions est vraie et l"autre est fausse. LorsquePetQsont simultan´ement vraies, la proposition (PouQ) est vraie, mais (Pou bienQ) est fausse.Nous n"utiliserons "ou" que dans le 1er sens.
Exercice -D´eterminer l"ensemble des r´eelsxv´erifiant la proposition :1.3. Implication
D´efinition 2.3 -SoientPetQdeux propositions. Alors (P=?Q) est une proposition. Elle est fausse lorsquePest vraie etQest fausse. Elle est vraie dans tous les autres cas. On l"´enonce "PimpliqueQ" ou "siP, alorsQ". Elle s"´enonce aussi "PentraineQ" , "pour queP,il faut queQ", "pour que Q,il suffit queP", "une condition n´ecessaire pour quePest queQ" ou "une condition suffisante pour queQest queP". !Dans le langage courant, on emploie souvent " il faut " `a la place de " il suffit ". Par exemple, on dit " pour traverser la rivi`ere, il faut prendre le bateau ", alors que c"est en fait suffisant, mais pas n´ecessaire. On peut le faire `a la nage. Proposition 2.4 -La proposition (P=?Q) a la mˆeme table de v´erit´e que la proposition ((nonP)ouQ).Exercice -Prouver cette proposition.
Exemples -Soitxun r´eel. Consid´erons la proposition (x= 2 =?x2= 4). Six?= 2, elle est vraie, parce qu"alors la proposition (x= 2) est fausse et six= 2 elle est vraie, parce qu"alors la proposition (x2= 4) est vraie. Cette proposition est donc toujours vraie. On l"´enonce aussi "sixest ´egal `a 2, alorsx2est ´egal `a 4". - 13 -Propositions
La proposition (x= 2 =?1 = 1) est vraie pour tout r´eelx, parce que (1 = 1) est vraie, mais il faut bien dire qu"elle n"a pas beaucoup d"int´erˆet. Il en est de mˆeme pour la proposition (1 = 0 =?2 = 3) qui est vraie, parce que la proposition (1 = 0) est fausse. !L"affirmation pr´ec´edente choque le sens courant. Cependant, on admet facilement que la proposition (x+ 1 =y=?x+ 3 =y+ 2) est vraie pour tous les r´eelsxety; et il suffit de prendrex=y= 0 pour obtenir (1 = 0 =?2 = 3). En fait, dans le langage courant, l"expression "PimpliqueQ" a souvent un autre sens : elle sous-entend quePest vraie et permet d"affirmer queQl"est aussi. Elle correspond donc en fait `a (Pet(P=?Q)).Il faut de mˆeme se m´efier de l"utilisation courante de "si" : la phrase "s"il fait beau, j"irai me promener" ou "j"irai me promener, s"il fait beau" sous-entend g´en´eralement "s"il ne fait pas beau, je n"irai pas me promener" (et correspond donc `a une´equivalence ((P=?Q)et(Q=?P)).
Exercice -Ecrire les implications suivantes en utilisant les symboles=?,≥, >,?=et dire si elles sont vraies pour tous les r´eelsx. 1 ◦) Pour quexsoit sup´erieur ou ´egal `a 1, il faut quexsoit strictement sup´erieur `a 2. 2 ◦) Pour quexsoit sup´erieur ou ´egal `a 1, il suffit quexsoit strictement sup´erieur `a 2. 3 ◦) Une condition n´ecessaire pour quexsoit sup´erieur ou ´egal `a1, est quexsoit diff´erent de 1.
4 ◦) Sixest dans l"intervalle[0,1], alorsx2-4x+ 3est positif.1.4. Equivalence
D´efinition 2.5 -SoientPetQdeux propositions. Alors, (P??Q) est une proposition. Elle est vraie lorsque les propositionsPetQsont toutes les deux vraies ou toutes les deux fausses. Elle est fausse dans les autres cas. On l"´enonce "Pest ´equivalente `aQ" ou "PetQsont ´equivalentes". Cette proposition s"´enonce aussi "Psi et seulement siQ", "pour queP,il faut et il suffit queQ", "une condition n´ecessaire et suffisante pour queQest que P". Dire quePetQsont ´equivalentes, c"est dire que ces propositions ont mˆemes valeurs de v´erit´e, c"est-`a-dire qu"elles signifient la mˆeme chose. Proposition 2.6 -SoientPetQdeux propositions. Alors, les deux propo- sitions (P??Q) et?(P=?Q)et(Q=?P)?ont mˆemes valeurs de v´erit´e. - 14 -ELEMENTS POUR COMPRENDRE UN ENONCE
Pour le voir, on peut ´ecrire la table de v´erit´e suivante :PQ(P=?Q)(Q=?P)(P??Q)
quotesdbs_dbs45.pdfusesText_45[PDF] a inclus dans b implique f(a) inclus dans f(b)
[PDF] combien f possède-t-il de sous ensembles ?
[PDF] padlet français
[PDF] paralangage exemple
[PDF] type de paralangage
[PDF] communication non verbale cours
[PDF] paralangage communication non verbale
[PDF] paralangage exercice
[PDF] le silence dans la communication non verbale
[PDF] le paralangage signifie communiquer sans parler
[PDF] définition élève en difficulté scolaire
[PDF] concept de souffrance
[PDF] concept douleur
[PDF] conflit latent définition
