 Chapitre 2 Ensembles et sous-ensembles
Chapitre 2 Ensembles et sous-ensembles
Ensembles et sous-ensembles. 1. Notion d'ensemble - Elément d'un ensemble. Dans une théorie mathématique il est rare qu'un objet intervienne seul ; d'o`u l
 Cours de mathématiques - Exo7
Cours de mathématiques - Exo7
Nous avons déjà vu que ceci est un espace vectoriel. Mini-exercices. Parmi les ensembles suivants reconnaître ceux qui sont des sous-espaces vectoriels : 1. (x
 COMBINATOIRE ET DÉNOMBREMENT
COMBINATOIRE ET DÉNOMBREMENT
×2 ( facteurs) possibilités d'obtenir un sous-ensemble de soit 2 . Exemple www.maths-et-tiques.fr/index.php/mentions-legales.
 Cours : Ensembles et applications
Cours : Ensembles et applications
les mathématiques sur des bases logiques. Il reçut une lettre d'un tout jeune cl(x) est donc un sous-ensemble de E on le note aussi x. Si y ∈ cl(x)
 [PDF] Groupes - Exo7 - Cours de mathématiques
[PDF] Groupes - Exo7 - Cours de mathématiques
4. Montrer que l'ensemble des matrices 2×2 de déterminant 1 ayant leurs coefficients dans Z est un sous-groupe de (Gl2×)
 Analyse combinatoire
Analyse combinatoire
6 mars 2008 Mathématiques Générales B. Université de Gen`eve. Sylvain Sardy. 6 mars ... – Combien y a-t-il de sous-ensembles d'un ensemble de cardinalité n?
 THÉORIE DES ENSEMBLES
THÉORIE DES ENSEMBLES
Soit Ω l'ensemble des nombres possibles d'obtenir de la somme de deux dés. Ω. 2
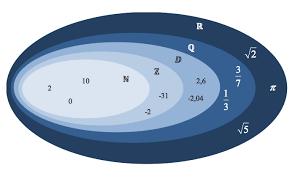 ENSEMBLES DE NOMBRES
ENSEMBLES DE NOMBRES
sous forme d'un intervalle : 2xГ3<4. 0 1. 0 1. 0 1. 0 1. 0 1. 0 1. 0 1. 0 1. Page 5. 5 sur 8. Yvan Monka – Académie de Strasbourg – www.maths-et-tiques.fr. 2xГ3 ...
 Chapitre 1 Ensembles et sous-ensembles
Chapitre 1 Ensembles et sous-ensembles
sous-ensembles d'un ensemble E. ... Il peut contenir des mots utilisés dans un sens différent du sens courant ou des mots spécifiques au langage mathématique.
 Chapitre 1 Ensembles et sous-ensembles
Chapitre 1 Ensembles et sous-ensembles
2?) Soit E un ensemble qui est la réunion de deux sous-ensembles on s'efforce souvent de les écrire en utilisant des symboles mathématiques.
 ENSEMBLES DE NOMBRES
ENSEMBLES DE NOMBRES
Un nombre rationnel peut s'écrire sous la forme d'un quotient a b avec a un entier et b un entier non nul. L'ensemble des nombres rationnels est noté ?.
 Cours : Ensembles et applications
Cours : Ensembles et applications
les mathématiques sur des bases logiques. Il reçut une lettre d'un tout jeune mathématicien : « J'ai bien lu votre premier.
 Cours de mathématiques - Exo7
Cours de mathématiques - Exo7
Sous-groupes. Montrer qu'un ensemble est un groupe à partir de la définition peut être assez long. Il existe une autre technique c'est de montrer qu'un
 Cours de mathématiques - Exo7
Cours de mathématiques - Exo7
L'ensemble F1 = (x y) ? 2
 Chapitre 1. Ensembles et applications.
Chapitre 1. Ensembles et applications.
18 févr. 2013 Soit f : A ?? B une application. Le sous-ensemble. {(xf (x))
 COMBINATOIRE ET DÉNOMBREMENT
COMBINATOIRE ET DÉNOMBREMENT
Alors est l'ensemble des couples possibles pour deux dés. On a par exemple : Page 3. Yvan Monka – Académie de Strasbourg – www.maths-et
 Chapitre 1 Ensembles et sous-ensembles
Chapitre 1 Ensembles et sous-ensembles
Ensembles et sous-ensembles. 1. Notion d'ensemble - Elément d'un ensemble. Un ensemble est une collection d'objets satisfaisant un certain nombre de
 Analyse combinatoire
Analyse combinatoire
6 mars 2008 Mathématiques Générales B. Université de Gen`eve ... distincts est un sous-ensemble `a k éléments de cet ensemble. Les éléments sont.
 Chapitre 2 Ensembles et sous-ensembles
Chapitre 2 Ensembles et sous-ensembles
Ensembles et sous-ensembles. 1. Notion d'ensemble - Elément d'un ensemble. Dans une théorie mathématique il est rare qu'un objet intervienne seul ; d'o`u
 [PDF] Chapitre 1 Ensembles et applications
[PDF] Chapitre 1 Ensembles et applications
18 fév 2013 · Pour un ensemble A l'ensemble de tous les sous-ensembles de A est noté 2A ou P(A) Exemple Soit A = {01} Les sous-ensembles de A sont ? A
 [PDF] Chapitre 1 Ensembles et sous-ensembles - Université de Rennes
[PDF] Chapitre 1 Ensembles et sous-ensembles - Université de Rennes
Définition 1 3 – Soient A et B deux sous-ensembles d'un ensemble E L'ensemble {x x ? A et x ? B} est appelé l'intersection des ensembles A
 [PDF] ensemblepdf
[PDF] ensemblepdf
Un ensemble est une collection d'objets satisfaisant un certain nombre de propriétés et chacun de ces objets est appelé élément de cet ensemble
 [PDF] THÉORIE DES ENSEMBLES
[PDF] THÉORIE DES ENSEMBLES
L'ensemble est dit un sous-ensemble de si et seulement si tous les éléments de sont aussi des éléments de On dit alors que l'ensemble est inclus dans l'
 [PDF] 1 Ensembles - Apprendre-en-lignenet
[PDF] 1 Ensembles - Apprendre-en-lignenet
Un sous-ensemble est un ensemble dont chaque élément est aussi contenu dans un autre ensemble Si A est un sous-ensemble de B on note A?B Par exemple si J
 [PDF] ENSEMBLES DE NOMBRES - maths et tiques
[PDF] ENSEMBLES DE NOMBRES - maths et tiques
Un nombre rationnel peut s'écrire sous la forme d'un quotient a b avec a un entier et b un entier non nul L'ensemble des nombres rationnels est noté ?
 [PDF] Généralités sur les ensembles - livres-mathematiquesfr
[PDF] Généralités sur les ensembles - livres-mathematiquesfr
Un des probl`emes qui nous intéressera rapidement est de déterminer tous les sous-ensembles d'un ensemble fini donné Pour cela nous avons besoin d'un ensemble
 [PDF] Introduction à la notion densembles - Université de Toulouse
[PDF] Introduction à la notion densembles - Université de Toulouse
Un ensemble est une collection d'objets deux à deux distincts appelés éléments On peut définir un ensemble de deux manières : en extension : on donne la liste
 [PDF] Ensembles et applications - Exo7 - Cours de mathématiques
[PDF] Ensembles et applications - Exo7 - Cours de mathématiques
que E est un sous-ensemble de F ou une partie de F • L'égalité E = F si et seulement si E ? F et F ? E • Ensemble des parties de E On note
 [PDF] Théorie des ensembles
[PDF] Théorie des ensembles
que pour tout ? ? E ? soit un sous-ensemble de E Voici un exemple : mathématique sur des ensembles qui s'exprime en quantifiant les variables et les
C'est quoi un sous-ensemble en maths ?
Étant donné un ensemble E; un sous-ensemble de E est un ensemble dont tous les éléments appartiennent à l'ensemble E. Synonyme de partie d'un ensemble. Un sous-ensemble propre ou strict d'un ensemble E est un sous-ensemble de E qui n'est pas égal à E.Quels sont les sous-ensembles ?
Un sous-ensemble est aussi un ensemble. Soient deux ensembles A et B. On dit que B est un sous-ensemble de A si tous les éléments de B sont aussi éléments de A. Exemple : L'ensemble B des entiers naturels de 1 à 3 est un sous-ensemble de l'ensemble A constitué par les entiers naturels de 1 à 7.Comment montrer qu'un ensemble est un sous-ensemble ?
Pour démontrer que F est un sous-espace vectoriel de E , on applique la caractérisation des sous-espaces vectoriels, c'est-à-dire qu'on vérifie que 0E?F 0 E ? F et que, pour tout couple (x,y)?F2 ( x , y ) ? F 2 et tout scalaire ??K ? ? K , on a {x+y?F?x?F.- On dit que A est inclus dans B si chaque élément de A est un élément de B. On note A ? B. On dit aussi “A est contenu dans B” ou “A est une partie de B” ou “A est un sous-ensemble de B”. Remarques - • A ? A • Si A ? B et B ? C, alors A ? C • A = B si et seulement si (A ? B et B ? A).
Chapitre 1. Ensembles et applications.
()February 18, 2013 1 / 47Table des mati`eres
1Ensembles: introduction
2Ensembles finis
()February 18, 2013 2 / 471. Ensembles: introduction
D´efinition
On appelleensembleune collection des objets. Ces objets sont appel´esles´el´ementsde l"ensemble.
Exemples
1)= l"ensemble de tous les nombres entiers positifs.
2)= l"ensemble de tous les nombres entiers relatifs.
3)= l"ensemble des nombres rationnelsm
n,mn,n= 0.4)= l"ensemble des nombres r´eels.
5)+= l"ensemble des nombres r´eels positifs.
6)= l"ensemble des nombres r´eels non nuls.
Terminologie de la th´eorie des ensembles
Sixest un ´el´ement d"un ensembleA, on ecritxA. Si non, on ´ecrit xA. Par exemple 2,2 3. ()February 18, 2013 3 / 47 On peut d´efinir un ensemble par la liste de ses ´el´ements. Par exemple, l"ensemble contenant le seul ´el´ement 0 est not´e0. L"ensemble contenant trois ´el´ements 123 est not´e par123. Une autre fa¸con de d´efinir un ensemble c"est d"indiquer la propri´et´e `a laquelle v´erifient tous les ´el´ements de cet ensemble et seulement ces´el´ements. L"ensemble de tous les ´el´ements v´erifiant propri´et´ePest not´e
xP.Exemple
l"ensemble de tous les nombres naturels strictement sup´erieurs`a 2 est not´e xx2D´efinition
L"ensemble ne contenant aucun ´el´ement est appel´el"ensemble videet not´e ()February 18, 2013 4 / 47D´efinition
SoitEFdes ensembles. Si chaque ´el´ement deEest aussi un ´el´ement de F, on dit queEestune partie (ou sous-ensemble)deFet on ´ecritEF. SiEFetE=Falors on dit queEest unsous-ensemble propredeE et on ´ecritEF.Exemples
1). 2).3) quel que soit un ensembleEon a:EetEE.
Pour un ensembleA, l"ensemble de tous les sous-ensembles deAest not´e 2AouP(A).
Exemple
SoitA=01. Les sous-ensembles deAsont,A,0,1donc
P(A) =0101.
()February 18, 2013 5 / 47D´efinition
SoitABdes ensembles. L"ensemble qui contient tous les ´el´ementsqui appartiennent `a la fois `aAet `aBest appel´el"intersection de ABet not´e AB.Autrement dit (xAB)((xA) et (xB)).
Exemple
01 21=1
D´efinition
SoitABdes ensembles. L"ensemble des ´el´ementsxtels quexAou xBest appell´ela r´eunion de A et Bet not´eAB.Exemple
On note parl"ensemble de tous les nombres entiers n´egatifs (y compris0). On a alors=et=0.
()February 18, 2013 6 / 47D´efinition
SiAEsont des ensembles, alors l"ensemblexExAest appel´e compl´ementaire de A dans E, et not´eEA.SiAE, l"ensembleEAest not´e aussiCA.
Exemple
Quel que soit un ensembleEon a:C=EetCE=.
R`egles de calcul
Intersection et r´eunion sont commutatives:
AB=BA,AB=BA,
et associatives:A(BC) = (AB)C,A(BC) = (AB)C
On a:AA=AA=A,A=,A=A.
()February 18, 2013 7 / 47Proposition
A(BC) = (AB)(AC)(l"intersection est distributive par rapport `a la r´eunion).D´emonstration.On va montrer d"abord que
A(BC)(AB)(AC).
SixA(BC), alorsxAetxBouxC. DoncxAet
xBou bienxAetxC. Autrement ditxABou xAC. Ce qui est ´equivalent `ax(AB)(AC). De la mˆeme fa¸con, on v´erifie que (AB)(AC)A(BC). Donc chacun de deux ensembles de notre ´enonc´e fait partie de l"autre.Cela veut dire qu"ils sont ´egaux.?
Exercice
Montrer queA(BC) = (AB)(AC)
()February 18, 2013 8 / 47Proposition
Soit E un ensemble et A, BE. Alors CAB=CACBet
CAB=CACB.
D´emonstration.Nous avons
xCAB (xAB) (xA)(xB)Par la loi de De Morgan on a
(xA)(xB) (xA) (xB) La derni`ere assertion est ´equivalente `a (xCA)(xCB), d"o`u xCABxCAB La d´emonstration de la deuxi`eme formule est similaire.?D´efinition
SoitABdes ensembles. L"ensemble de tous les couples ordonn´es (xy) tels quexA,yBest appell´ele produit cart´esiendeAetB, not´e AB. ()February 18, 2013 9 / 47Exemple
A=,B=alorsAB=est identifi´e avec le plan euclidien. (faire le dessin!) NB. L"ordre de deux composantes d"un couple est important: (xy)= (yx) comme on le voit sur le dessin.Remarque
Nous avons d´ecrit quelques proc´edures pr´ecises qui permettent de construire des nouveaux ensembles `a partir des ensembles d´ej`a existants. Il se trouvent que toutes les fa¸cons de construire des ensembles ne sont pas bonnes. On peut montrer par exemple quel"ensemble de tous les ensembles n"existe pas, c"est-`a-dire l"hypoth`ese de l"existence de cet ensemble m`ene `a une contradiction. ()February 18, 2013 10 / 47Applications
D´efinition
SoitABdes ensembles. Une loi qui associe `a chaque ´el´ementxdeAun unique ´el´ementydeBest appell´eeapplicationoufonctiondeAdansB.On ´ecrit
f:ABouAf?? B Pour un ´elementxAl"´el´ement deBqui lui est associ´e est not´ef(x), et on ´ecritx??? f(x). L"´el´ementf(x) est appel´el"image de x par fetx est ditl"ant´ec´edentdef(x).Exemples
1)f??d´efinie par la formulef(x) = sin(x) est une application de
dans. L"´el´ement 0a un nombre infini d"ant´ec´edents, notamment, pour toutkle nombrekest un ant´ec´edent de 0.2) La formulef(n) =n2d´efinit une application dedans lui-mˆeme.
()February 18, 2013 11 / 47 Dans les exemples pr´ec´edents les fonctions ont ´et´e d´efinies par des formules (polynˆomiales, trigonom´etriques etc.); ce n"est pas un seul moyen de d´efinir des fonctions comme le montre l"exemple suivant.Fonction de Dirichlet::?,
(x) = 1six (x) = 0sixD´efinition
Soitf:A?Bune application. Le sous-ensemble
(xf(x))xA ABest ditle graphe de fet not´e Γf.Exemples
1) Soitf:la fonction donn´ee par:f(x) =x. Alors son graphe Γf
est une ligne droite dans le plan euclidien2, notamment la bissectrice de l"angle droit form´e de deux axes de coordonn´ees. (faire les dessins!)2) Soitf:la fonction donn´ee par:f(x) = 0. Alors son graphe Γf
est l"axe des abscisses. ()February 18, 2013 12 / 47D´efinition
Soitf:A??Bg:B??Cdes applications. L"application deA dansCqui associe `a chaquexAl"´el´ementg(f(x)) deCest appel´ee l"application compos´ee(o`u simplementla compos´ee) defetg, et not´ee gf.Exemple
Soitf:l"application d´efinie par la formulef(x) =x3. Alors pour l"applicationg=ffon ag(x) = (x3)3=x27.Exercice
Calculerfgo`ufg:R+R+sont les applications suivantes:1)f(x) =xg(x) =1
x;2)f(x) =1
xg(x) =1x;3)f(x) =1
xg(x) =1x2. ()February 18, 2013 13 / 47Remarque
En g´eneralfg=gfmˆeme sifgsont des applications d"un ensemble Adans lui-mˆeme. Par example, sif(x) =x3g(x) = 2x(des applications dedans) on a (fg)(x) = 8x3(gf)(x) = 2x3D´efinition
SoitAun ensemble, etBA. L"application qui `a chaque ´el´ementxB associexlui-mˆeme consid´er´e comme un ´el´ement deAest appel´ee l"application inclusion. SiB=Acette application est appel´eel"application identit´edeAet not´eeIdA.D´efinition
Soitf:ABune application, etAA. La compos´ee de l"application inclusion et defest appel´eela restriction de f sur Aet not´ee fA:AA.C"est-`a-dire (fA)(x) =f(x) pour toutxA.
()February 18, 2013 14 / 47D´efinition
Une applicationf:A?Best diteinjectivesi
f(x) =f(y) =(x=y) (c"est-`a-dire sizBadmet un ant´ec´edent dansA, alors cet ant´ec´edent est unique.)D´efinition
Une applicationf:A?Best ditesurjectivesi:
zBxAtel quef(x) =z (c"est-`a-dire chaquezdansBadmet un ant´ec´edent dansA).Exemples
1)f(x) = sin(x) n"est pas injective carf(0) =f() = 0 et n"est pas
surjective carxsin(x)?1. ()February 18, 2013 15 / 472) En revanche, la fonctionh:?[?1;1] d´efinie parh(x) = sin(x) est
surjective.3) La fonctiong:?g(n) =n2est injective mais elle n"est pas
surjective (v´erifiez!).Graphe d"une fonction surjective:
pour chaqueyla droitelyintersecte le graphe Γf. (faire les dessins!)Graphe d"une fonction f injective:
Chaque droitelyintersecte Γfune fois maximum.
D´efinition
Une application qui est injective et surjective est ditebijective(ouune bijection). Doncfest bijective si et seulement si chaqueyBadmet un unique ant´ec´edent dansA. ()February 18, 2013 16 / 47Exemples
1)f:?f(x) =?xest bijective (car chaqueyadmet un
unique ant´ec´edent par rapport `af, notamment?y).2) On va construire une bijection???
. Posons (x) = x2sixest pair;
x+12sixest impair
V´erifions queest injective.
Supposons que(x) =(y) alors
si(x)?0 alorsxest pair,yaussi etx2=y2, soitx=y.
si(x)0 alorsxetysont impairs et?x+12=?y+12=x=y.
V´erifions queest surjective.
Soitnalorsn=(2n), 2n.
Soitmm0. Alorsm=(?2m?1) o`u?2m?1.
()February 18, 2013 17 / 47Remarque
L"ensembleest un sous-ensemble propre de, c"est-`a-dire, et =. Cependant on a ´etabli une bijection entreetce qui veut dire quecontient "autant d"´elements" que.3) L"application
f: [01][02];f(t) = 2t est une bijection. ( Rappelons que [ab] =xa?x?b. ) En effet, montrons d"abord quefest injective. Sif(x) =f(y), alors2x= 2yce qui impliquex=y. Montrons maintenant quefest surjective.
Soity[02]. Posonsx=y2, alorsx[01] etf(x) = 2x=y.
Exercice
Soitabnombres r´eels etab. Montrer que l"application g: [01][ab];f(t) =a+t(b?a) est bijective. ()February 18, 2013 18 / 47D´efinition
Soitf:A?Bune application.
SoitXA, alors le sous-ensemble
yBy=f(x)pour unxX est appel´el"image de X par f, not´eImX. L"image deAest not´e aussi parIm(f).fest surjective si et seulement siIm(f) =Y.
SoitYB, le sous-ensemble
xAf(x)Y est appel´el"image r´eciproque de Y par fnot´ef1(Y). ()February 18, 2013 19 / 47Exemple
Soitf:?,f(x) =x2. AlorsIm(f) =Im() =+et
f1(1) =?1;1.
Proposition
1) La compos´ee de2applications injectives est injective.
2) La compos´ee de2applications surjectives est surjective.
3) La compos´ee de2applications bijectives est bijective.
D´emonstration.1) SoitAf??
Bg??Co`ufgsont des
applications injectives. Pour montrer quegfest injective, supposons que (gf)(x) = (gf)(y), pourxyA. Alorsg(f(x)) =g(f(y)). Puisquegest injective, cela implique f(x) =f(y). De plus,f´etant injective, on d´eduitx=y.Donc (gf) est injective.
2) SoitAf??
Bg??C, o`ufgsont des applications surjectives.
SoitzC. L"applicationg´etant surjective, il existeyBtel que g(y) =z. ()February 18, 2013 20 / 47 De plus,f´etant surjective, il existexAtel quef(x) =y. Finalementz=g(y) =g(f(x)) = (gf)(x) et l"applicationgfest surjective.3) d´ecoule de 1) et 2).?
D´efinition
(Rappel). SoitAun ensemble. On noteIdAl"applicationAAd´efinie parIdA(x) =x. On l"appellel"application identit´e.Proposition
Soit f:A?B une application. Alors f est bijective si et seulement si il existe une application g:B?A, telle que gf=IdAetfg=IdB g est appel´ee l"application r´eciproque `a f , et not´ee f 1.D´emonstration.
Premi`erement, supposons qu"il existeg:B?A, tel quefg=IdB, gf=IdA, et montrons quefest bijective. ()February 18, 2013 21 / 47 Remarquons quefest injective. En effet, sif(x) =f(y) alors g(f(x)) =g(f(y)) donc (gf)(x) = (gf)(y). Or (gf)(x) =IdB(x) =x, de mˆeme poury; doncx=y. De plusfest surjective, car siyB,y=IdB(y) = (fg)(y) =f(z), avecz=g(y), doncyf(A). On en d´eduit quefest bijective.Deuxi`emement, soitf:A??
Bune bijection.
AlorsyB,xAtel quef(x) =y(carfest surjective). On pose g(y) =x(un telxest unique, puisquefest injective) et on obtient ainsi une applicationg:B?? A.Par d´efinition on a (gf) =IdA, (fg) =IdB.
Corollaire
Il existe une bijection g:??.
()February 18, 2013 22 / 472 . Ensembles finis
D´efinition
Soitn?1 un entier positif. On note par [[1n]] l"ensemble12n.Proposition
Soit nk.
1) S"il existe une application injective[[1n]]?[[1k]]alors n?k.
2) S"il existe une application surjective[[1n]]?[[1k]]alors n?k.
3) S"il existe une application bijective[[1n]]?[[1k]]alors n=k.
D´emonstration.1) R´ecurrence surn.
Initialisation.Sin= 1, alorsk?1 =n, cark.
H´er´edit´e.On suppose que notre proposition est d´ej`a d´emontr´ee au rang n. Soitf: [[1n+ 1]]?[[1k]] une application injective. Supposons d"abord quef(n+ 1) =k.f´etant injective, on af(s)k poursn+ 1, doncf([[1n]])[[1k?1]], et on obtient une application injective [[1n]][[1k?1]]. Par l"hypoth´ese de r´ecurrence,n?k?1 doncn+ 1?k. ()February 18, 2013 23 / 473) Supposons mantenant quef(n+ 1) =set 1?s?k?1.
Soit: [[1k]]?[[1k]] une bijection d´efinie par la formule suivante: (x) =x si x=sx=k; k si x=s; s si x=k; C"est-`a-dire,permute les ´el´ementssetket laisse fixe tous les autres´el´ements de [[1k]].
L"application (f) est injective (en tant que la compos´ee de deux applications injectives).De plus (f)(n+ 1) =(f(n+ 1)) =(s) =k;
en applicant `afle raisonnement pr´ec´edent on obtientn+ 1?k.Exercice
D´emontrer 2).
Le point 3) d´ecoule de 1) et 2).?
()February 18, 2013 24 / 47D´efinition
Une ensembleEest appel´eensemble fini, si pour certainnil existe une bijectionf: [[1n]]?E, ou siEest vide. Le nombrenest appel´ela cardinalit´e de Eoule cardinal de E, not´e card(E) ouE. Par convention on posecard() = 0. Autrement dit un ensemble est fini s"il existe une suite finiea1an, (aiE) telle que chaque ´el´ement deEapparaˆıt une seule fois dans cette suite. La donn´ee d"une bijectionf: [[1n]]?Eest ´equivalente `a celle d"une telle suite:ai=f(i).Remarque
Pour un ensemble finiEle nombrenci-dessus est unique. En effet si on a deux bijections [[1n]]f??Eg??[[1k]]
alorsg1f: [[1n]]?? [[1k]] est une bijection, doncn=k. ()February 18, 2013 25 / 47Exemple
L"ensemble de tous les nombres entiers positifsntels quenest pair et n20 est fini, et sa cardinalit´e est ´egale `a 10.Exemple
L"ensemble de tous le nombres naturelsn"est pas fini. En effet, supposons qu"il existe une bijectionf: [[1n]]?pour certain n. Consid`erons l"application inclusiong: [[1n+ 1]]. La composition def1avecgserait une application injective f1g: [[1n+ 1]]?[[1n]]
ce qui est impossible. ()February 18, 2013 26 / 47Propri´et´es des cardinaux des ensembles finis(les d´emonstrations seront omises ou juste esquiss´ees).1) SiAest un ensemble fini, etf:ABune bijection, alorsBest
´evidemment un ensemble fini, etcardA=cardB.
Cette propri´et´e est importante:s"il y a une bijection entre deux ensembles, alors leurs cardinalit´es sont les mˆemes; il y a autant d"´el´ements dans l"un que dans l"autre.2) SoitAun ensemble fini, etBA. AlorsBest un ensemble fini et
cardB?cardA.Corollaire
,,,ne sont pas finis. D´emonstration.Chacun de ces ensemble contient l"ensemble infini.? ()February 18, 2013 27 / 473) SoitA,Bdes ensembles finis. AlorsABetABsont des ensembles
finis et on a cardAB=cardA+cardB?cardAB (faire un dessin!)4) SoitA,B,Cdes ensembles finis, alorsABCest un ensemble fini
et on a (en appliquant la formule pr´ec´edente) card(ABC) =card((AB)C) = =cardAB+cardC?card((AB)(AC)) or card((AB)(AC)) =card(AC)+card(AB)?card(ABC)Finalement
card(ABC) =cardA+cardB+cardC ?card(AB)?card(AC)?card(BC) +card(ABC) ()February 18, 2013 28 / 47Exercice
Calculercard(ABCD) en fonction des cardinalit´es des ensemblesABCDet leurs intersections.
Plus g´en´eralement, calculercard(A1An).
Proposition
Soit A, B des ensembles finis. Alors AB est un ensemble fini et cardAB=cardAcardB. D´emonstration.SoitA=a1an,B=b1bm, alorscardA=n, cardB=m. ()February 18, 2013 29 / 47 Les ´el´ements deABpeuvent ˆetre arrang´es dans un tableau rectangulairenm: (a1b1) (a1b2)(a1bm) (a2b1) (a2b2)(a2bm) (anb1) (anbm) On auranlignes etm´el´ements dans chaque ligne. Donc au totalnm´el´ements.?
Proposition
Soit X, Y des ensembles finis non vides.
1) Soit f:X??
Y une application injective. Alors
cardX?cardY et sicardY=cardX, alors f est une bijection.2) Soit g: X
Y une application surjective. Alors
cardX?cardY et sicardY=cardX, alors g est une bijection. ()February 18, 2013 30 / 47 D´emonstration.1) Soitn=cardX, alors il existe une application bijective h: [1n]??X. De mˆeme, soitm=cardY, etk: [1m]??Y
quotesdbs_dbs45.pdfusesText_45[PDF] a inclus dans b implique f(a) inclus dans f(b)
[PDF] combien f possède-t-il de sous ensembles ?
[PDF] padlet français
[PDF] paralangage exemple
[PDF] type de paralangage
[PDF] communication non verbale cours
[PDF] paralangage communication non verbale
[PDF] paralangage exercice
[PDF] le silence dans la communication non verbale
[PDF] le paralangage signifie communiquer sans parler
[PDF] définition élève en difficulté scolaire
[PDF] concept de souffrance
[PDF] concept douleur
[PDF] conflit latent définition
