[PDF] Formulaire danalyse vectorielle

View - Download Formulaire danalyse vectorielle

Previous PDF

Next PDF

Fiche méthode

Mathématiques

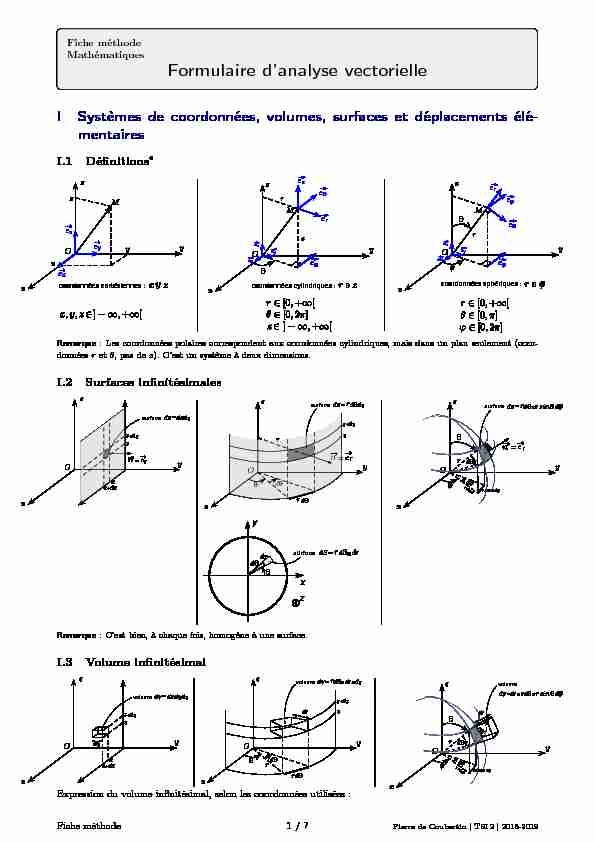
Formulaire d"analyse vectorielleISystèmes de co ordonnées,volumes, surfaces et déplacements élé-

mentaires I.1

Définitions

xyz O e xyz O e z e r xyz O e x e z e y M e x e z e y e r zM e x e z e y e e r r M e e r zcoordonnées cylindriques : r coordonnées sphériques : zcoordonnées cartésiennes : xy y xz

Remarque :Les coordonnées polaires correspondent aux coordonnées cylindriques, mais dans un plan seulement (coor-

donnéesret, pas dez). C"est un système à deux dimensions. I.2

Surfaces infinitésimales

xyz O x dxx+ zdz z surface dS dxdz= xyz O d n e y= n e r r r d zdz z surface dSdz=r d xyz O r d d n e r surface dS=r d dsinr sin r dsinr r d xy z d dr surface =r d dSdrRemarque :C"est bien, à chaque fois, homogène à une surface. I.3

V olumeinfinitésimal

xyz O x dxx+ zdz z volumedV dxdy=dz dy xyz O d r r d zdz z volumedVdz=r d dr dr xyz O r d d volume dV=rddsinr sin r dsinr r d dr drExpression du volume infinitésimal, selon les coordonnées utilisées : Fiche méthode1 / 7Pierre de Coubertin | TSI2 | 2018-2019 •Cartésiennes: dV=dxdydz. •Cylindriques : dV=rdrddz. •Sphériques : dV=r2sindrdd'.

Remarque :C"est bien, à chaque fois, homogène à un volume. On remarque aussi que dVest donné par le produit des

composantes du vecteur!dl(cf ci-dessous). I.4

V ecteurdéplacemen tinfinitésimal

Expression du vecteur déplacement infinitésimal, selon les coordonnées utilisées : •Cylindriques :!dl=dr~er+rd~e+dz~ez. •Sphériques :!dl=dr~er+rd~e+rsind'~e'.

La même chose avec possibilité de faire bouger la figure, et d"afficher l"élément de surface et de volume :

Remarque :

•pour obtenir l"élément de volume, il faut multiplier les trois composantes du vecteur!dl;

•pour obtenir l"élément de surface dSdont la normale est l"un des trois vecteurs de la base, il faut multiplier les

deux autres composantes de!dl. II

Champs scalaire e tvecto riel,intégrales

II.1

Définitions

•Un champ scalaire est une fonction qui, à tout pointMde l"espace, associe un nombre. Mathématiquement, c"est donc une fonctionf:R3!R.

Exemples :le potentiel électrostatiqueV(M), la pressionp(M), l"indice optiquen(M), sont des champs

scalaires. •Un champ vectoriel est une fonction qui, à tout pointMde l"espace, associe un vecteur.

Mathématiquement, c"est donc une fonction

~A:R3!R3.

Exemples :le champ électrique~E(M), le champ magnétique~B(M), la champ des vitesses~v(M), sont des

champs vectoriels. II.2

V ariationinfinitésimale

Pour une fonction d"une seule variable on connaît f(x+dx) =f(x) +df f(x+dx) =f(x) +f0(x)dxPour un champ scalaire (donc à trois variables), ceci devient f(x+dx;y+dy;z+dz) =f(x;y;z) +df f(x+dx;y+dy;z+dz) =f(x;y;z) +@f@x dx+@f@y dy+@f@z dz(et il existe des expressions similaires en coordonnées cylindriques ou sphériques)

Cette dernière expression indique comment évoluef(x;y;z)si on l"évalue un peu plus loin, plus précisément en

un point décalé du vecteur!dl=dx~ex+dy~ey+dz~ezpar rapport au point(x;y;z). Si on utilise la définition du gradient en coordonnées cartésiennes, on voit qu"on a : gradf!dl=@f@x dx+@f@y dy+@f@z dz=df Fiche méthode2 / 7Pierre de Coubertin | TSI2 | 2018-2019 On en déduit le théorème reliant gradient et variation infinitésimale df=!gradf!dlConséquences : •On a B

A!gradf!dl=

B A

df=f(B)f(A):•Si df >0, c"est que!gradfet!dlsont plutôt dans le même sens : le gradient pointe vers les zones oùf

augmente.

•Si df= 0, c"est que!gradfet!dlsont perpendiculaires : le gradient est perpendiculaire aux surfaces

f=cst. II.3 In tégralessur un v olume,une surface, un con tour Ici,fdésigne un champ scalaire quelconque et~Aun champ vectoriel quelconque. Sur un contour ou cheminNotationCe que c"estVariantes et remarquesExemples cette année B

A(C)f(M)dlintégrale de la quantitéf(M)le

long d"un chemin ou contourC rejoignant les pointsAetB. C f(M)dl: même chose mais le contour est fermé (il boucle sur lui-même).

Attention, il faut préciser dans

quel sens parcourir le contour.chemin optique (AB) =B

A(C)n(M)dl

longueur d"une courbe L AB=B

A(C)dl

B2 B

1(C)~A(M)!dlintégrale de la quantité

~A(M)le long d"un chemin ou contourC rejoignant les pointsB1etB2.

Aétant un champ vectoriel, on

parle de lacirculationde~Ale long du contourC. C ~A(M)!dl: même chose mais le contour est fermé.

Attention, il faut préciser dans

quel sens parcourir le contour.circulation du champ

électrique

C=B

A(C)~E(M)!dl

circulation du champ magnétique (th. d"Ampère)B

A(C)~B(M)!dl

travail d"une force B

A(C)~F!dlSur une surface

NotationCe que c"estVariantes et remarquesExemples cette année S f(M)dSintégrale de la quantitéf(M) sur la surfaceS. S f(M)dS: même chose mais la surface est fermée.Expression de la surface : S= SdS S f(M)!dSintégrale de la quantitéf(M) sur la surfaceS. dS=dS~navec~nle vecteur normal à la surface.

Attention, la surfaceSest

orientée : il faut indiquer où est la normale extérieure.idem

Expression de la résultante

des forces de pression : ~F= Sp!dS S ~A!dSintégrale de ~A!dSsur la surface S.

Il s"agit dufluxdu champ de

vecteur~Aà travers la surfaceS. dS=dS~navec~nle vecteur normal à la surface.

Attention, la surfaceSest

orientée : il faut indiquer où est la normale extérieure. S ~A!dS: même chose mais la surface est fermée.

Normale sortante par

conventionFlux de ~Edans le théorème de Gauss :~E=

S~E!dS

Débit volumique

D v=

S~v!dS

Débit massique

D

S~v!dS

Flux thermique

th=

S~jth!dS

IntensitéI=

S~j!dSFiche méthode3 / 7Pierre de Coubertin | TSI2 | 2018-2019

Sur un volume

NotationCe que c"estVariantes et remarquesExemples cette année V f(M)dVintégrale de la quantitéf(M) sur le volumeV.Expression du volume : V= VdV

Masse totaleM=

VdV

Charge totaleQ=

VdVII.4Théorèmes de Stok eset d"Ostrogradski •Théorème de Stokes-Ampère : C ~A!dl= S (!rot~A)!dSIci ~Aest un champ vectoriel quelconque.Cest un contour fermé orienté.Sest une surface qui s"appuie sur le contourC, orientée dans le sens direct par rapport àC (règle de la main droite).z x y

0•Théorème d"Ostrogradski :

S ~A!dS= V (div~A)dVIci ~Aest un champ vectoriel quelconque.Sest la surface fermée qui entoure le volumeV, et sa normale est sortante. z x y

0Remarque :

•On a également le théorème du gradient, qui sert par exemple à démontrer la formule d"Archimède : dans la même situation que pour Ostrogradski, on a S f!dS= V (!gradf)dVIIIOp érateursrotationnel, divergence, gradient, laplacien III.1 Expression des op érateursen co ordonnéescartésienn es (tout le contenu de cette partie : à connaître ou à savoir retrouver rapidement)

f(x;y;z)est un champ scalaire quelconque.~A(x;y;z)est un champ vectoriel quelconque. Pour alléger les

notations des dérivées partielles, on ne note pas les variables qui sont gardées fixées, mais elles sont sous-

entendues.

On note les vecteurs avec la notation

~A= A x A y A z=Ax~ex+Ay~ey+Az~ez

On introduit le "vecteur" nabla :

~r= @@x @@y @@z . Ce n"est pas vraiment un vecteur. C"est un moyen pratique de

retrouver les formules des différents opérateurs en coordonnées cartésiennes (mais pas forcément pour les autres

systèmes de coordonnées). Fiche méthode4 / 7Pierre de Coubertin | TSI2 | 2018-2019

OpérateurRemarque

importanteExpression en coordonnées cartésiennesComment le retrouver avec nabla

Gradient

gradfs"applique à unscalaire retourne un vecteur @f@x @f@y @f@z rf= @@x @@y @@z f= @f@x @f@y @f@z

Divergence

div ~As"applique à unvecteur retourne un scalaire@A x@x +@Ay@y +@Az@z ~r~A= @@x @@y @@z A x A y A z=@Ax@x +@Ay@y +@Az@z

Rotationnel

rot~As"applique à unvecteur retourne un vecteur @A z@y @Ay@z @A x@z @Az@x @A y@x @Ax@y r ^~A= @@x @@y @@z A x A y A z= @A z@y @Ay@z @A x@z @Az@x @A y@x @Ax@y

Laplacien

scalaire f= div!gradfs"applique àquotesdbs_dbs32.pdfusesText_38

[PDF] analyse vectorielle exercices corrigés physique

[PDF] livre d anglais 1am algerie 2016

[PDF] sujet danglais de 2eme année lycée langue

[PDF] anglais 1as scientifique

[PDF] cours 1ere année anglais lmd

[PDF] bts industriels exemples dossiers ccf anglais

[PDF] expression oral anglais bts

[PDF] vocabulaire anglais administratif

[PDF] anglais des affaires cours gratuits

[PDF] english business communication pdf

[PDF] cours d'anglais 1ere année universitaire st

[PDF] la phonétique et la phonologie pdf

[PDF] cours de phonétique française

[PDF] cours de phonétique française s1 pdf

[PDF] exercice phonétique français pdf