Exercice 1 Considérons un échantillon de n = 5 individus où chaque
Calculer les écarts types σj de chacune des variables. 4. Calculer la matrice Z des données centrées-réduites. 5. Calculer la matrice de variance-covariance Σ
Exercices corrigés
2. En déduire les lois marginales de U et V . 3. Calculer les matrices de covariance de [X Y ]t et de [U V ]t
Exercices
En général une matrice de variances-covariances inversible est la matrice d'un produit Les notations sont celles de l'exercice précédent. a) Pour quelle ...
Régression linéaire
vecteur aléatoire ˆβ ou matrice de variance-covariance
Corrigés des exercices
Exercice 4. Solution. 1 La matrice de variance-covariance est donnée par V =.. 0 01000 0
TD01- COUPLES DE VARIABLES ALEATOIRES DISCRETES ET
=2X – Y Montrer que (U
coefficient de corrélation Exercice 6 : Matrice de variance-covariance
Exercice 6 : Matrice de variance-covariance. En Matlab il y a une commande « cov » pour calculer la matrice de variance-covariance pour des réalisations des
Sciences de gestion - Synthèse de cours exercices corrigés
.... . La matrice de variance et de covariance de u est : Σu = E(uui) =..... σ2. 1 σ12. ··· σ1m σ21 σ2. 2. ··· σ2m ... ... ... .
Se familiariser avec les bases/notations Exercice 1. Soient une
Donnez la matrice de variance–covariance des variables indicatrices 1{kœS}. k = yk
Master 1 BEM MQEM T. D. n II . LACP pratique. Exercice n 1. Ent
2) Calculer la covariance entre x1 et x1. Que représente cette quantité? Exercice n? 2 ... et V la matrice de variance-covariance. Après calculs :.
Exercice 1 Considérons un échantillon de n = 5 individus où chaque
Calculer les écarts types ?j de chacune des variables. 4. Calculer la matrice Z des données centrées-réduites. 5. Calculer la matrice de variance-covariance ?
Exercices corrigés
Calculer la variance Var{X1} de X1 et la covariance Cov{X1X2} de (X1
Exercices et problèmes de statistique et probabilités
Corrigés des exercices . Chapitre 5 Estimateur sans biais de variance minimale . ... f) Matrice des variances-covariances. M(XY) =.
1 Matrice de covariance
Typiquement son espérance ou sa variance. Un estimateur de ? est une variable aléatoire ?? à valeurs dans Rd
Exercices
Les variances et les covariances sont toutes égales. ? La matrice de corrélation est de rang 2. ? L'angle entre deux variables vaut au maximum 2.
TD 1 : Se familiariser avec les bases/notations Exercice 1. Soient
Ce qui est logique puisque nous avons vu que le fi–estimateur était un estimateur sans biais ! Exercice 3. Soit la matrice de variance–covariance. = (k¸)k¸ des
Corrigés des exercices
Corrigés des exercices Note : Dans la note de l'exercice 1.1 on a établi que P(X < x) = FX(x ... La matrice des variances-covariances est :.
PC 5 – Calcul de lois & Vecteurs gaussiens
20 mai 2019 Exercice 1. ... Le calcul du déterminant de la matrice jacobienne donne ... matrice de variance-covariance est donnée par. Var(U) = Var.
coefficient de corrélation Exercice 6 : Matrice de variance-covariance
Vos prévisions sont-elles vérifiées ? Exercice 6 : Matrice de variance-covariance. En Matlab il y a une commande « cov » pour calculer la
[PDF] Exercice 1 Considérons un échantillon de n = 5 individus où chaque
Calculer la matrice de variance-covariance ? de Z et la matrice de corrélation R de X Commenter 6 Effectuer une décomposition spectrale de la matrice de
[PDF] coefficient de corrélation Exercice 6 : Matrice de variance-covariance
Exercice 6 : Matrice de variance-covariance En Matlab il y a une commande « cov » pour calculer la matrice de variance-covariance pour des
[PDF] Exercices
La fiche donne des énoncés d'exercices d'algèbre et d'analyse des données En général une matrice de variances-covariances inversible est la matrice
[PDF] Exercices corrigés - IMT Atlantique
Le lecteur trouvera ici les énoncés et corrigés des exercices proposés dans Calculer les matrices de covariance de [X Y ]t et de [U V ]t Solution
[PDF] Corrections des exercices - Pages personnelles Université Rennes 2
Exercice 5 1 (Questions de cours) A A C B Exercice 5 2 (Analyse de la covariance) Nous avons pour le modèle complet la matrice suivante : X =
[PDF] Leçon 14 Exercices corrigés
Leçon 14 Exercices corrigés L'objet de l'exercice est d'obtenir un bon encadrement de la dans R3 de matrice de covariance
[PDF] 1 Matrice de covariance - Mathématiques
Typiquement son espérance ou sa variance Un estimateur de ? est une variable aléatoire ?? à valeurs dans Rd qui dépend de X1 Xn Il est consistant
[PDF] CORRIGÉ
CORRIGÉ TD 9 : Régression linéaire Exercice 1 : On reprend l'exemple des 5 Calculs effectués pour variances et covariance : Var(x) = µ(x2 ) ? µ(x)
[PDF] Synthèse de cours exercices corrigés - ACCUEIL
Sciences de gestion Synthèse de cours Exercices corrigés Économétrie Q où Ln est la matrice de variance et de covariance de u (?u = Ln)(3) et où Q
Comment trouver la matrice des variances covariances ?
D'ailleurs, la covariance d'une variable avec elle-même (autocovariance) est tout simplement la variance. Cov(X,X) = V(X). Donc, faisons un parallèle avec le théorème de König : la covariance est la moyenne du produit des valeurs de deux variables moins le produit des deux moyennes.Comment montrer qu'une matrice est une matrice de covariance ?
Propriétés de la matrice de covariance
La matrice de covariance est symétrique ; ses éléments diagonaux sont les variances et les éléments extra-diagonaux sont les covariances des couples de variables. La matrice de covariance est semi-définie positive (ses valeurs propres sont positives ou nulles).Comment Calculer COV ?
On calcule Cov( ? X , ? Y ) = E( ? X ? Y ) ? E( ? X ) E( ? Y ) = ? ? E( X Y ) ? ? ? E( X ) E( Y ).- En termes simples, les deux termes mesurent la relation et la dépendance entre deux variables. “Covariance” = la direction de la relation linéaire entre les variables. La “corrélation”, en revanche, mesure à la fois la force et le sens de la relation linéaire entre deux variables.
![[PDF] Exercice 1 Considérons un échantillon de n = 5 individus où chaque](https://pdfprof.com/Listes/17/80712-17td-partie-4-corr.pdf.pdf.jpg "[PDF] Exercice 1 Considérons un échantillon de n = 5 individus où chaque")
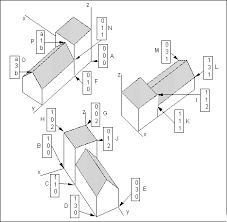
Université de CaenTDs Partie 4Analyse de données UFR des SciencesPar Faïcel Chamroukhi 2017/2018Exercice 1Considérons un échantillon den= 5individus où chaque individuxi2Rdest décrit
pard= 3variables réelles. Cet échantillon est représenté par la matriceX= (x1;x2;x3;x4;x5)t
suivante : X=p10BBBBBBBB@2 2 3
3 1 2 1 0 3 2 1 42 1 31
CCCCCCCCA
On va faire une ACP centrée réduite de ce jeu de données. Calculer l"individu mo yen(le cen trede gra vitédu n uagede données)Calculer la matrice Ydes données centrées
Calculer les écarts t ypesjde chacune des variables Calculer la matrice Zdes données centrées-réduites Calculer la matrice de v ariance-covariancedeZet la matrice de corrélationRdeX.Commenter.
Effectuer une décomp ositionsp ectralede la matrice de corrélation R: déterminer les valeurs
propresjassociées aux vecteurs propres non-nulsujdeR. Déterminer les facte ursprincipaux fjet les axes principauxajdu nuage des individus.Vérifier leurs propriétés statistiques
Calculer p ourc hacundes axes factoriels ,l"inertie du jeu de données pro jetéessur l"axe considéré, et la part d"inertie qu"il explique. Calculer les comp osantesprincipales cjpour les individus. Comment s"interprètent les com-posantes principales en fonction des variables de départ. Vérifier leur propriétés statistiques.
10. Représen tergraphiquemen tle n uagedes in dividussur le plan factoriel défini p arles deux premiers axes factoriels. Commenter. 11. Représen tergraphiquemen tle n uagedes v ariablessur le plan factoriel défini par les deux premiers axes factoriels. Commenter.Solution 1
L"individu mo yenest obten uen faisan tla mo yennedes lignes du tableau X:x=Pn i=1xi=n=p10(2;1;3)T La matrice Ydes données centrées est obtenue en soustrayant à chaque ligne deXla moyenneY=X(x;x;x;x;x)T=p10
BBBBBBBB@0 1 0
1 01 11 0 0 0 10 0 01
CCCCCCCCA
3.Le calcul des écarts-t ypej(racines carrées des variances2j) de chacune des variables peut
se faire de deux façons. La première en appliquant la définition de la variance pour chaque variable : j=v uut1 i=1(xijxj)2=v uut1 i=1y 2ij pourj= 1;:::;3etn= 5. La deuxième en calculant directement la matrice de variances-covariances et en exploitant ainsi la formulation vectorielle on trouve directement toutes les variances (et donc les écarts type) car celles-ci sont les éléments diagonaux de la matrice de variances-covariances : X=1n i=1(xix)(xix)T=1n i=1y iyTi=1nYTY=105
BB@2 11
1 2 01 0 21
CCA=0BB@4 22
2 4 02 0 41
CCA donc= (1;2;3)T= (2;2;2)T La matrice Zdes données centrées-réduites est de terme généralzij=xijxj j=yij j. Cela revient donc à diviser chaque colonne deYpar l"écart type de la variable correspondante : Z=p10BBBBBBBB@0 1 0
1 01 11 0 0 0 10 0 01
CCCCCCCCA=
La matrice de v ariance-covariancedeZ:Zétant la matrice centrée-réduite deXdonc sa matrice de covariance de terme correspond à la matrice de corrélation deX. En effet : =1n i=1(ziz)(ziz)T=1n i=1z izT=1n i=112 yi12 yT=1n i=1(xix2 )(xix2 R=1n i=1(xix )(xix )T=1n i=1(xix2 )(xix2 )T= carZest centrée et donc sa moyenne suivant les ligneszest le vecteur nul. Pour le calcul on trouve donc : =R=15ZTZ=15
104BB@2 11
1 2 01 0 21
CCA=0BB@1 1=21=2
1=2 1 0
1=2 0 11
CCA L"A CPcen tréeréduite nécessite le calcul des v aleurspropres jassociées aux vecteurs propres non-nulsujde la matrice de corrélationR. On résout l"équationRu=u. Pour les valeurs propres, cela revient à résoudre le système det(RI) = 0:11=21=21=2 10
1=2 0 1
= (1) 0 1 1=21=21=2
0 1 1=21=21=2
= (1)(1)214 (1)14 (1) = (1)(1)212 = (1)(11p2 )(1+1p2 et on obtient les trois valeurs propres (selon l"ordre décroissant) :1= 1+1p2 ;2= 1;3= 11p2 P ourdéterminer les v ecteurspropres ujon résoutRu=u. En posantu= (x;y;z)t, on a, pour2= 1:BB@1 1=21=2
1=2 1 0
1=2 0 11
CCA0 BB@x CCA=0 BB@x CCA)8 >>:x+12 y12 z=x x+y=y x+z=zquotesdbs_dbs7.pdfusesText_5[PDF] exercice aire et périmètre 3eme
[PDF] exercices corrigés arithmétique 3eme
[PDF] relations interspécifiques exercices
[PDF] relations interspécifiques exemples
[PDF] exercice sur les facteurs biotiques
[PDF] démontrer que deux triangles sont isométriques
[PDF] triangles isométriques démonstrations
[PDF] triangles isométriques exercices corrigés
[PDF] figures isométriques et semblables exercices
[PDF] triangles isométriques exercices corrigés 4ème
[PDF] figures isométriques exercices
[PDF] isométrie exercices corrigés
[PDF] exercices corrigés dioptre sphérique
[PDF] exercice sur le pluriel des noms composés
